Tipos y profundidad de bits#
Outline del capítulo
La profundidad de bits y el tipo de una imagen determinan los valores de píxel que puede contener
Una imagen con mayor profundidad de bits puede contener (potencialmente) más información.
Durante la adquisición, la mayoría de las imágenes tienen el tipo entero sin signo.
Durante el procesamiento, a menudo es mejor utilizar tipos de punto flotante.
Si se intenta almacenar valores fuera del rango permitido por el tipo y la profundidad de bits, se produce un recorte, que suele ser muy malo.
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Como se describe en Imágenes y píxeles, cada píxel tiene un valor numérico, pero un píxel no puede tener cualquier valor numérico. En su lugar, trabaja bajo las restricciones del tipo y profundidad de bits de la imagen.
En última instancia, los píxeles se almacenan en algún formato binario: una secuencia de bits (binary digits), es decir, unos y ceros. La profundidad de bits determina cuántos de estos unos y ceros están disponibles para almacenar cada píxel. El tipo determina cómo se interpretan estos bits.
Representar números con bits#

Figura 20 Bob ideando su código.#
Supongamos que Bob está desarrollando un código secreto para almacenar números, pero en el que sólo se le permite escribir unos y ceros. Si sólo se le permite escribir un único uno o cero (es decir, un único bit), no tiene muchas opciones.
Suponiendo que quiere que sus números codificados sean enteros consecutivos empezando por cero, esto significa que sólo puede representar dos números diferentes: uno y cero.
Show code cell source
import numpy as np
import pandas as pd
n_bits = 1
df = pd.DataFrame([(ii, np.binary_repr(ii, n_bits)) for ii in range(2**n_bits)], columns=('Decimal', 'Binary'))
df.style.hide(axis='index')
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
Si se le permite un bit extra, de repente puede representar 4 números combinando los unos y los ceros de forma diferente.
Show code cell source
import numpy as np
import pandas as pd
n_bits = 2
df = pd.DataFrame([(ii, np.binary_repr(ii, n_bits)) for ii in range(2**n_bits)], columns=('Decimal', 'Binary'))
df.style.hide(axis='index')
| Decimal | Binary |
|---|---|
| 0 | 00 |
| 1 | 01 |
| 2 | 10 |
| 3 | 11 |
Evidentemente, cuantos más bits se le permitan a Bob, más combinaciones únicas podrá tener y, por tanto, más números diferentes podrá representar en su código.
Con 8 bits a su disposición, Bob puede combinar los bits de 256 formas distintas para representar 256 números diferentes.
Show code cell source
import numpy as np
import pandas as pd
n_bits = 8
df = pd.DataFrame([(ii, np.binary_repr(ii, n_bits)) for ii in range(2**n_bits)], columns=('Decimal', 'Binary'))
df.style.hide(axis='index')
| Decimal | Binary |
|---|---|
| 0 | 00000000 |
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
| 4 | 00000100 |
| 5 | 00000101 |
| 6 | 00000110 |
| 7 | 00000111 |
| 8 | 00001000 |
| 9 | 00001001 |
| 10 | 00001010 |
| 11 | 00001011 |
| 12 | 00001100 |
| 13 | 00001101 |
| 14 | 00001110 |
| 15 | 00001111 |
| 16 | 00010000 |
| 17 | 00010001 |
| 18 | 00010010 |
| 19 | 00010011 |
| 20 | 00010100 |
| 21 | 00010101 |
| 22 | 00010110 |
| 23 | 00010111 |
| 24 | 00011000 |
| 25 | 00011001 |
| 26 | 00011010 |
| 27 | 00011011 |
| 28 | 00011100 |
| 29 | 00011101 |
| 30 | 00011110 |
| 31 | 00011111 |
| 32 | 00100000 |
| 33 | 00100001 |
| 34 | 00100010 |
| 35 | 00100011 |
| 36 | 00100100 |
| 37 | 00100101 |
| 38 | 00100110 |
| 39 | 00100111 |
| 40 | 00101000 |
| 41 | 00101001 |
| 42 | 00101010 |
| 43 | 00101011 |
| 44 | 00101100 |
| 45 | 00101101 |
| 46 | 00101110 |
| 47 | 00101111 |
| 48 | 00110000 |
| 49 | 00110001 |
| 50 | 00110010 |
| 51 | 00110011 |
| 52 | 00110100 |
| 53 | 00110101 |
| 54 | 00110110 |
| 55 | 00110111 |
| 56 | 00111000 |
| 57 | 00111001 |
| 58 | 00111010 |
| 59 | 00111011 |
| 60 | 00111100 |
| 61 | 00111101 |
| 62 | 00111110 |
| 63 | 00111111 |
| 64 | 01000000 |
| 65 | 01000001 |
| 66 | 01000010 |
| 67 | 01000011 |
| 68 | 01000100 |
| 69 | 01000101 |
| 70 | 01000110 |
| 71 | 01000111 |
| 72 | 01001000 |
| 73 | 01001001 |
| 74 | 01001010 |
| 75 | 01001011 |
| 76 | 01001100 |
| 77 | 01001101 |
| 78 | 01001110 |
| 79 | 01001111 |
| 80 | 01010000 |
| 81 | 01010001 |
| 82 | 01010010 |
| 83 | 01010011 |
| 84 | 01010100 |
| 85 | 01010101 |
| 86 | 01010110 |
| 87 | 01010111 |
| 88 | 01011000 |
| 89 | 01011001 |
| 90 | 01011010 |
| 91 | 01011011 |
| 92 | 01011100 |
| 93 | 01011101 |
| 94 | 01011110 |
| 95 | 01011111 |
| 96 | 01100000 |
| 97 | 01100001 |
| 98 | 01100010 |
| 99 | 01100011 |
| 100 | 01100100 |
| 101 | 01100101 |
| 102 | 01100110 |
| 103 | 01100111 |
| 104 | 01101000 |
| 105 | 01101001 |
| 106 | 01101010 |
| 107 | 01101011 |
| 108 | 01101100 |
| 109 | 01101101 |
| 110 | 01101110 |
| 111 | 01101111 |
| 112 | 01110000 |
| 113 | 01110001 |
| 114 | 01110010 |
| 115 | 01110011 |
| 116 | 01110100 |
| 117 | 01110101 |
| 118 | 01110110 |
| 119 | 01110111 |
| 120 | 01111000 |
| 121 | 01111001 |
| 122 | 01111010 |
| 123 | 01111011 |
| 124 | 01111100 |
| 125 | 01111101 |
| 126 | 01111110 |
| 127 | 01111111 |
| 128 | 10000000 |
| 129 | 10000001 |
| 130 | 10000010 |
| 131 | 10000011 |
| 132 | 10000100 |
| 133 | 10000101 |
| 134 | 10000110 |
| 135 | 10000111 |
| 136 | 10001000 |
| 137 | 10001001 |
| 138 | 10001010 |
| 139 | 10001011 |
| 140 | 10001100 |
| 141 | 10001101 |
| 142 | 10001110 |
| 143 | 10001111 |
| 144 | 10010000 |
| 145 | 10010001 |
| 146 | 10010010 |
| 147 | 10010011 |
| 148 | 10010100 |
| 149 | 10010101 |
| 150 | 10010110 |
| 151 | 10010111 |
| 152 | 10011000 |
| 153 | 10011001 |
| 154 | 10011010 |
| 155 | 10011011 |
| 156 | 10011100 |
| 157 | 10011101 |
| 158 | 10011110 |
| 159 | 10011111 |
| 160 | 10100000 |
| 161 | 10100001 |
| 162 | 10100010 |
| 163 | 10100011 |
| 164 | 10100100 |
| 165 | 10100101 |
| 166 | 10100110 |
| 167 | 10100111 |
| 168 | 10101000 |
| 169 | 10101001 |
| 170 | 10101010 |
| 171 | 10101011 |
| 172 | 10101100 |
| 173 | 10101101 |
| 174 | 10101110 |
| 175 | 10101111 |
| 176 | 10110000 |
| 177 | 10110001 |
| 178 | 10110010 |
| 179 | 10110011 |
| 180 | 10110100 |
| 181 | 10110101 |
| 182 | 10110110 |
| 183 | 10110111 |
| 184 | 10111000 |
| 185 | 10111001 |
| 186 | 10111010 |
| 187 | 10111011 |
| 188 | 10111100 |
| 189 | 10111101 |
| 190 | 10111110 |
| 191 | 10111111 |
| 192 | 11000000 |
| 193 | 11000001 |
| 194 | 11000010 |
| 195 | 11000011 |
| 196 | 11000100 |
| 197 | 11000101 |
| 198 | 11000110 |
| 199 | 11000111 |
| 200 | 11001000 |
| 201 | 11001001 |
| 202 | 11001010 |
| 203 | 11001011 |
| 204 | 11001100 |
| 205 | 11001101 |
| 206 | 11001110 |
| 207 | 11001111 |
| 208 | 11010000 |
| 209 | 11010001 |
| 210 | 11010010 |
| 211 | 11010011 |
| 212 | 11010100 |
| 213 | 11010101 |
| 214 | 11010110 |
| 215 | 11010111 |
| 216 | 11011000 |
| 217 | 11011001 |
| 218 | 11011010 |
| 219 | 11011011 |
| 220 | 11011100 |
| 221 | 11011101 |
| 222 | 11011110 |
| 223 | 11011111 |
| 224 | 11100000 |
| 225 | 11100001 |
| 226 | 11100010 |
| 227 | 11100011 |
| 228 | 11100100 |
| 229 | 11100101 |
| 230 | 11100110 |
| 231 | 11100111 |
| 232 | 11101000 |
| 233 | 11101001 |
| 234 | 11101010 |
| 235 | 11101011 |
| 236 | 11101100 |
| 237 | 11101101 |
| 238 | 11101110 |
| 239 | 11101111 |
| 240 | 11110000 |
| 241 | 11110001 |
| 242 | 11110010 |
| 243 | 11110011 |
| 244 | 11110100 |
| 245 | 11110101 |
| 246 | 11110110 |
| 247 | 11110111 |
| 248 | 11111000 |
| 249 | 11111001 |
| 250 | 11111010 |
| 251 | 11111011 |
| 252 | 11111100 |
| 253 | 11111101 |
| 254 | 11111110 |
| 255 | 11111111 |
Los valores de los píxeles de una imagen se almacenan mediante un código como éste. Cada valor posible se representa en binario como una combinación única de bits.
Profundidad de bits de la imagen#
La profundidad de bits de una imagen es el número de bits utilizados para representar cada píxel. Una profundidad de bits de 8 indica que se utilizan 8 bits para representar el valor de un píxel.
La profundidad de bits impone un límite a los valores de píxel posibles. Una menor profundidad de bits implica que hay menos valores de píxel disponibles, lo que puede dar como resultado una imagen que contenga menos información.
Show code cell source
fig = create_figure(figsize=(10, 4))
im = load_image('sunny_cell.tif')
assert im.dtype == np.uint16
def rescale_to_bits(im: np.ndarray, n_bits: int) -> np.ndarray:
"""
Helper method to rescale an image to have values supported with a specific bit-depth (unsigned integer).
"""
max_value = 2**n_bits - 1
im = im - im.min()
im = im * (max_value / im.max())
im = np.round(im)
return im
# Show images converted (with rescaling) to different bit-depths
bit_depths = [1, 2, 4, 8]
n = len(bit_depths)
for ii, bits in enumerate(bit_depths):
im_bits = rescale_to_bits(im, bits)
show_image(im_bits, title=f"{bits}-bit", pos=(2, n, ii+1))
show_histogram(im_bits, ylabel=None, bins=range(0, 2**bits+1), align='left', pos=(2, n, n+ii+1))
plt.xticks([0, 2**bits-1])
# plt.yticks([])
plt.tight_layout()
glue_fig('fig_bit_depths_demo', fig)
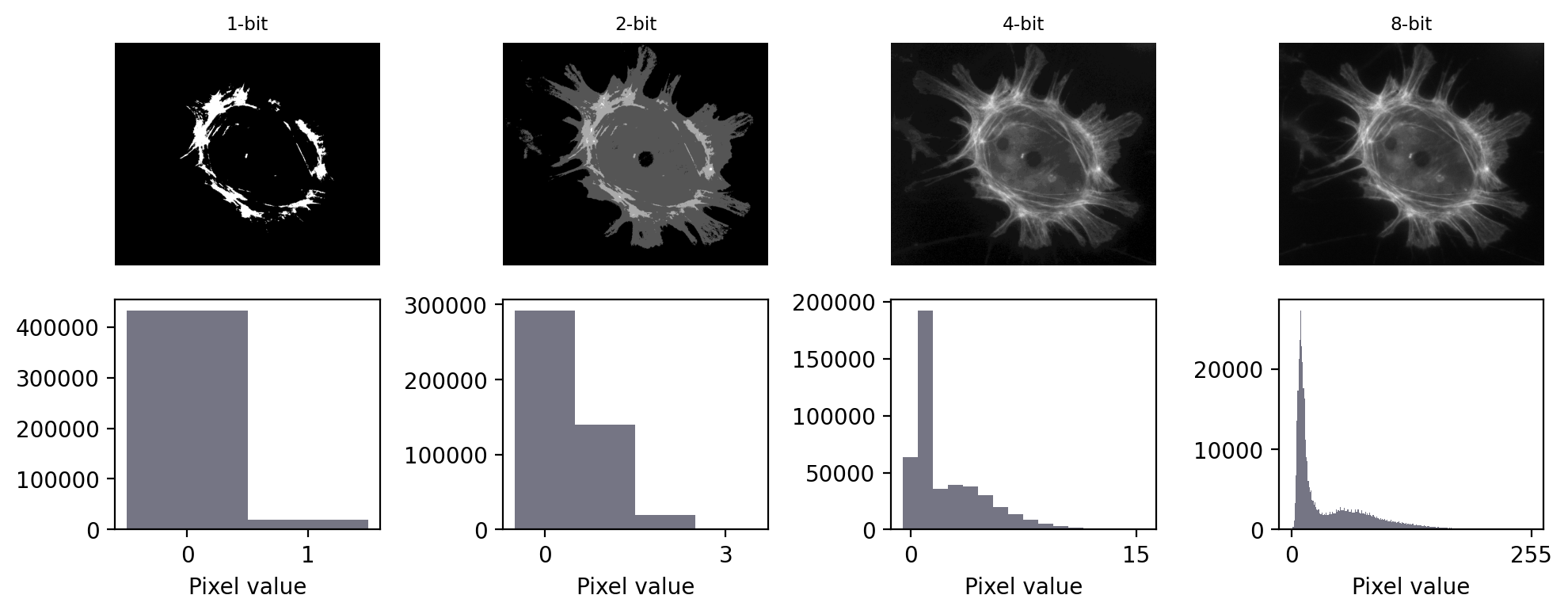
Figura 21 Representación de una imagen utilizando diferentes profundidades de bits.#
Como se muestra en Figura 21, una imagen de 1 bit sólo puede contener dos valores: aquí, mostrados como píxeles blancos o negros. Tales imágenes binarias son extremadamente limitadas en la información que pueden contener, aunque resultarán muy útiles más adelante al procesar imágenes.
Una imagen de 2 bits no es mucho mejor, ya que sólo contiene, como máximo, 4 valores diferentes. Una imagen de 4 bits puede tener 16 valores. Cuando se visualiza con una LUT de escala de grises, es una mejora sustancial. De hecho, el ojo no es particularmente bueno distinguiendo diferentes tonos de gris, por lo que es difícil ver mucha diferencia entre una imagen de 4 bits y una de 8 bits. Sin embargo, los histogramas revelan que la imagen de 8 bits contiene información más detallada.
En la práctica, los ordenadores suelen trabajar con grupos de 8 bits, y cada grupo de 8 bits se conoce como byte. Los microscopios que adquieren imágenes de 8 bits siguen siendo razonablemente comunes, y éstos permiten 28 = 256 valores de píxel diferentes, que caen en el rango 0-255. El siguiente paso es una imagen de 16 bits, que puede contener 216 = 65536 valores: una mejora espectacular (0-65535).
¿Qué impacto esperas que tenga la profundidad de bits en el tamaño del archivo de una imagen guardada?
Por ejemplo, ¿esperarías que una imagen de 8 bits tuviera un tamaño de archivo mayor, menor o (aproximadamente) equivalente al de una imagen de 16 bits de la misma escena? Puedes suponer que las dos imágenes tienen el mismo número de píxeles.
En general, se espera que el tamaño del archivo necesario para almacenar una imagen sea mayor con una mayor profundidad de bits.
Suponiendo que la imagen no esté comprimida, una imagen de 16 bits necesitaría aproximadamente el doble de espacio de almacenamiento que una imagen correspondiente de 8 bits.
Si tienes una imagen de 1024 x 1024 píxeles y 8 bits, necesitarás aproximadamente 1 MB para almacenarla. La imagen de 16 bits correspondiente necesitaría aproximadamente 2 MB.
Tipo de imagen#
Llegados a este punto, puede que te preguntes: ¿y las fracciones? ¿O los números negativos?
En realidad, la profundidad de bits es sólo una parte de la historia. El tipo de la imagen es lo que determina cómo se interpretan los bits.
Hasta ahora, hemos supuesto que se utilizarían 8 bits para representar números enteros en el rango 0 – 255, porque tenemos 28 = 256 combinaciones diferentes de 8 bits. Esta es una representación de entero sin signo.
Pero supongamos que dedicamos uno de nuestros bits a representar si el número debe interpretarse como positivo o negativo, y que los siete bits restantes proporcionan la magnitud del número. Una imagen que utilice este enfoque tiene el tipo entero con signo. Típicamente, un entero con signo de 8 bits puede estar en el rango -128 – 127. Incluyendo el 0, aún quedan 256 posibilidades distintas.
Aunque las imágenes que adquirimos se componen normalmente de enteros sin signo, más adelante exploraremos las inmensas ventajas de procesar operaciones como promediar o restar valores de píxeles, en cuyo caso los píxeles resultantes pueden ser negativos o contener partes fraccionarias. Las imágenes de tipo punto flotante permiten almacenar estos nuevos valores, no necesariamente enteros, de forma eficiente. Eso puede ser importante, porque podríamos perder mucha información si tuviéramos que redondear siempre los valores de los píxeles a enteros.
Las imágenes de punto flotante también nos permiten almacenar tres valores especiales: \(+\infty\), \(-\infty\) y NaN. El último de ellos significa Not a Number, y puede representar un valor omitido o imposible, por ejemplo, el resultado de 0/0.
Mensaje clave
La profundidad de bits y el tipo de imagen determinan los valores de píxel posibles.
Cómo y por qué pueden flotar los puntos
Los valores de píxeles en punto flotante tienen una precisión variable en función de si representan números muy pequeños o muy grandes.
Representar un número en binario utilizando punto flotante es análogo a escribirlo en forma estándar, es decir, algo así como 3,14×108, que puede escribirse como 3,14e8. En este caso, hemos conseguido representar 314000000 utilizando sólo 4 dígitos: 314 y 8 (el 10 ya está incorporado en la representación).
En el caso binario, la forma es más propiamente algo como ± 2M×N: tenemos un bit dedicado al signo, un número fijo de bits adicionales para el exponente M, y el resto al número principal N (llamado fracción).
Un número en punto flotante de 32 bits utiliza normalmente 1 bit para el signo, 8 bits para el exponente y 23 bits para la fracción, lo que nos permite almacenar una gama muy amplia de números positivos y negativos. Un número en punto flotante de 64 bits utiliza 1 bit para el signo, 11 bits para el exponente y 52 para la fracción, lo que permite un rango aún más amplio y una mayor precisión. Pero, de nuevo, éstos requieren más espacio de almacenamiento que los de 8 y 16 bits.
Tipos de imagen y profundidad de bits más comunes
Son posibles muchas permutaciones de profundidad de bits y tipo de bits, pero en la práctica las más habituales para las imágenes son tres:
Entero sin signo de 8 bits
Entero sin signo de 16 bits
punto flotante de 32 bits
Las representaciones anteriores son lo suficientemente ubicuas como para que a menudo se asuma el tipo. A menos que se especifique lo contrario, es más probable que cualquier imagen de 8 o 16 bits utilice números enteros sin signo, mientras que una imagen de 32 bits probablemente utilice píxeles de punto flotante.
Es posible que puedas tener una imagen entera de 32 bits con/sin signo, o incluso una imagen de punto flotante de 16 bits, pero son menos comunes en la naturaleza.
Los píxeles que se muestran a la derecha pertenecen todos a imágenes diferentes.
En cada caso, identifica qué tipo posible podría tener una imagen para representar el valor del píxel. Puede haber más de un tipo posible para cada píxel.
Sus opciones de tipo son:
Entero con signo
Entero sin signo
Punto flotante
Los posibles tipos de imágenes, de izquierda a derecha:
Entero con signo o punto flotante
Entero sin signo, entero con signo o punto flotante
Punto flotante
Ten en cuenta que el “punto flotante” es una opción en todos los casos: es la representación más flexible.
¿Cuál es el valor máximo de píxeles que se puede almacenar en una imagen de 16 bits, entero sin signo?
El valor máximo que se puede almacenar en una imagen entera sin signo de 16 bits es 216-1 = 65535.
¿Cuál sería el valor máximo de píxeles que se puede almacenar en una imagen de 16 bits, entero con signo?
El valor máximo que se puede almacenar en una imagen entera con signo de 16 bits es 215-1 = 32767 ( como uno de los bits se usa para el signo, nos quedan 15).
¿Una imagen como matriz de números, o solo unos y ceros?
Quizás recuerdes cómo Figura 3 mostraba una imagen como una matriz de números. Esto ya es un nivel ligeramente alto de abstracción de cómo se representa realmente la imagen. Es más exacto ver la imagen (o, de hecho, cualquier dato digital) como si fuera simplemente un largo flujo de unos y ceros, como
“00011001000111110010111100111101001000000010000000011010001000000010001100101110001001000010100000101010010010000011001000011000001001000100001000111011001010110001111000100110000111010100000100110100000111100011001000100100001111000010101000110001001000010010001001001110010000110001011100100011001101000011001100110111001010100011111001010011001011110010100000110000001010100011111100111010010010100100011001010000001111010101111101011101011011000101010110010100101011011110110000111110010001110100111000101101…”
Se necesita más información sobre cómo se codifican los valores de píxeles de la imagen para interpretar estos unos y ceros. Esto incluye cómo se deben dividir los unos y los ceros para representar diferentes valores (por ejemplo, en trozos de 8, 16 o algún otro número).
La profundidad de bits es lo que nos dice qué tan grandes son los fragmentos y el tipo nos dice cómo convertir cada fragmento en un número decimal.
Cuando las cosas van mal#
Ahora estamos listos para discutir por qué es absolutamente necesario conocer los conceptos básicos de las profundidades de bits y los tipos de imágenes cuando se trabaja con imágenes científicas.
El punto principal de Imágenes y píxeles es que debemos mantener el control de los valores de nuestros píxeles para que nuestro análisis final sea justificable. Hay dos cosas principales relacionadas con los bits que pueden salir mal al intentar almacenar un valor de píxel en una imagen:
Recorte: Intentamos almacenar un número fuera del rango admitido, de modo que se almacene el valor válido más cercano. Por ejemplo, si intentamos almacenar -10 en una imagen entera sin signo de 8 bits, entonces el valor más cercano que podemos almacenar es 0. De manera similar, si intentamos almacenar 500, entonces el valor válido más cercano es 255.
Redondeo: Intentamos almacenar un número que no se puede representar exactamente, por lo que se debe redondear al valor más cercano posible. Por ejemplo, si queremos almacenar 6.4 en una imagen entera sin signo de 8 bits, esto no es posible; más bien, necesitaríamos almacenar 6.
Recorte de datos#
De los dos problemas, el recorte suele ser el más grave, como se muestra en Figura 22. Una imagen recortada contiene píxeles con valores iguales al máximo o mínimo admitido por esa profundidad de bits, y ya no es posible saber qué valores deberían tener esos píxeles. La información se pierde irremediablemente.
El recorte suele ocurrir cada vez que se convierte una imagen para que tenga una profundidad de bits más baja. Durante esta conversión, es posible que no se conserven todos los valores de píxeles originales, en cuyo caso deben transformarse de alguna manera al rango permitido por la profundidad de bits de salida.
Esta transformación podría implicar simplemente recortar los valores no admitidos (normalmente muy malos), o podría implicar reescalar primero los valores de píxeles (normalmente menos malos).
Show code cell source
fig = create_figure(figsize=(10, 10))
im = load_image('sunny_cell.tif')
# Define the maximum in the 16-bit image (so that it more clearly illustrates the concepts we want to show...)
# (Reader, please ignore this!)
max_value = 800
min_value = 32
im = im.astype(np.float32)
im = im - im.min()
im = im / im.max()
im = im * (max_value - min_value) + min_value
im = im.astype(np.uint16)
# Define colormap & display range
cmap = 'magma'
row = im.shape[0]//2
# vmax = np.percentile(im, 99)
vmax = im.max()
hist_params = dict(bins=100)
line_params = dict(y=row, color=(1, 1, 1), dashes=(4, 2))
# Original image
show_image(im, vmin=0, vmax=vmax, cmap=cmap, title="16-bit original", pos=431)
plt.axhline(**line_params)
show_image(im, vmin=0, vmax=im.max(), cmap=cmap, pos=434)
plt.axhline(**line_params)
plt.subplot(4, 3, 7)
prof_rescaled = im[row, :]
plt.plot(prof_rescaled)
plt.xlabel('x location')
plt.ylabel('Value')
plt.ylim(0, max_value)
show_histogram(im, **hist_params, pos=(4,3,10))
# Clipped to 255
im_clipped = np.clip(im, 0, 255)
show_image(im_clipped, vmin=0, vmax=vmax, cmap=cmap, title="8-bit clipped", pos=432)
plt.axhline(**line_params)
show_image(im_clipped, vmin=0, vmax=im_clipped.max(), cmap=cmap, pos=435)
plt.axhline(**line_params)
plt.subplot(4, 3, 8)
prof_rescaled = im_clipped[row, :]
plt.plot(prof_rescaled)
plt.xlabel('x location')
plt.ylabel('Value')
plt.ylim(0, max_value)
show_histogram(im_clipped, **hist_params, pos=(4,3,11))
# Rescaled, then clipped to 255
im_rescaled = np.clip(im*(255.0/im.max()), 0, 255)
show_image(im_rescaled, vmin=0, vmax=vmax, cmap=cmap, title="8-bit scaled", pos=433)
plt.axhline(**line_params)
show_image(im_rescaled, vmin=0, vmax=im_rescaled.max(), cmap=cmap, pos=436)
plt.axhline(**line_params)
plt.subplot(4, 3, 9)
prof_rescaled = im_rescaled[row, :]
plt.plot(prof_rescaled)
plt.xlabel('x location')
plt.ylabel('Value')
plt.ylim(0, max_value)
show_histogram(im_rescaled, **hist_params, pos=(4,3,12))
plt.tight_layout()
glue_fig("clipping_fig", fig)
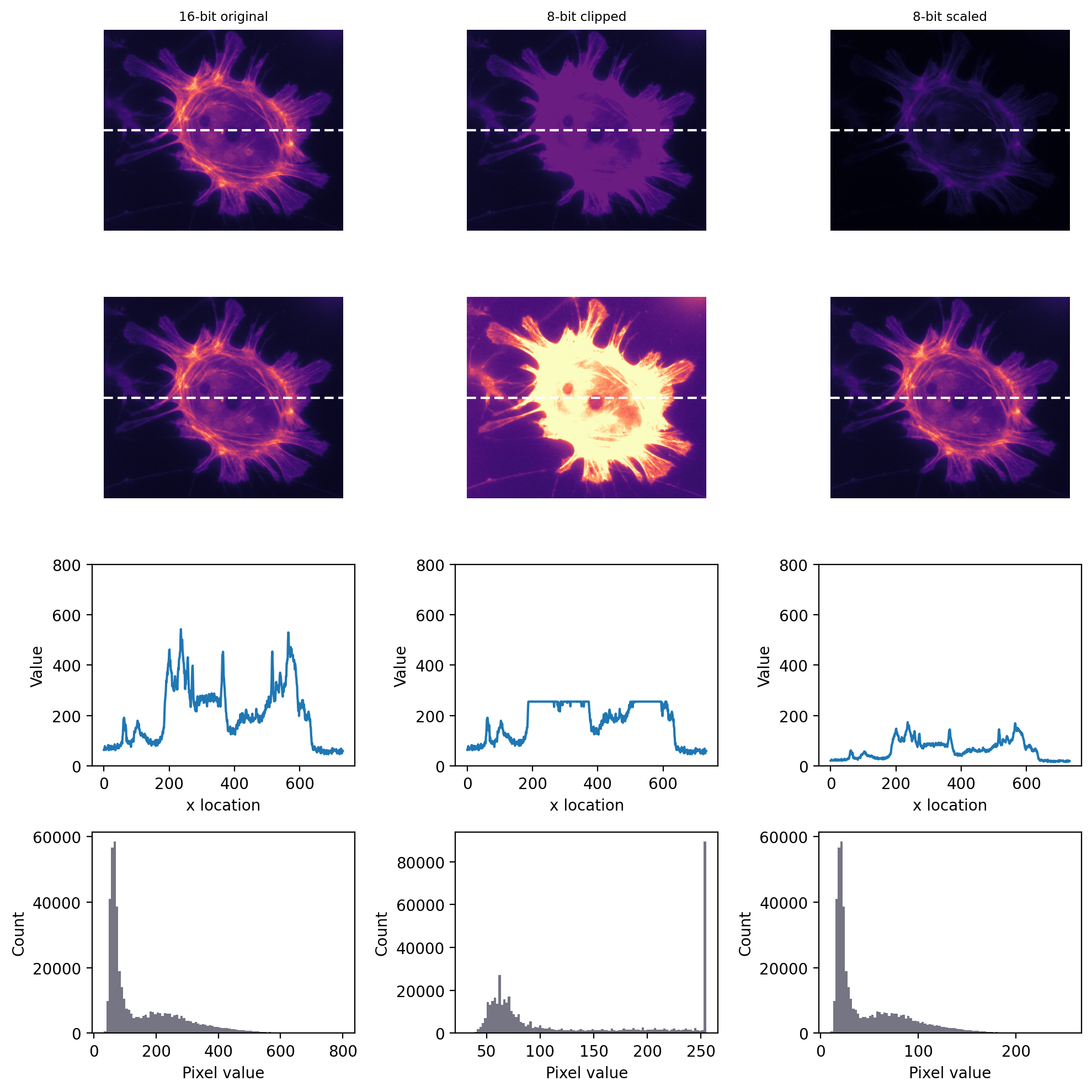
Figura 22 Almacenar una imagen usando una profundidad de bits más baja, ya sea recortando o escalando los valores. La fila superior muestra todas las imágenes con los mismos valores mínimo y máximo para determinar el contraste, mientras que la segunda fila muestra las mismas imágenes con el máximo establecido en el valor de píxel más alto realmente presente (las imágenes son las mismas, solo los LUT son diferentes). Las filas inferiores muestran un gráfico de los valores de píxeles a través del centro de cada imagen e histogramas de todos los valores de píxeles de la imagen. Se puede inferir que la información se perdió en ambas imágenes de 8 bits, pero de manera mucho más terrible cuando se aplicó el recorte. El reajuste comprime los datos en un rango estrecho, lo que podría dar lugar a algunos errores de redondeo. Pero la mayor parte de la información permanece intacta, y las formas del gráfico del perfil y del histograma siguen siendo similares.#
Sin embargo, es importante saber que el recorte ya puede ocurrir durante la adquisición de la imagen. En microscopía de fluorescencia, esto depende de tres factores principales:
La cantidad de luz que se emite. Debido a que los valores de los píxeles dependen de la cantidad de luz que se detecta, es menos probable que una muestra que emita muy poca luz requiera la capacidad de almacenar valores muy grandes. Aunque todavía podría debido a…
La ganancia del microscopio. Cuantificar con precisión cantidades muy pequeñas de luz tiene dificultades prácticas. La ganancia de un microscopio amplifica efectivamente la cantidad de luz detectada para ayudar a superar esto antes de convertirla en un valor de píxel (consulte Microscopios y detectores). Sin embargo, si la ganancia es demasiado alta, incluso una pequeña cantidad de fotones detectados podrían terminar sobreamplificados hasta que se produzca el recorte.
El offset del microscopio. Esto actúa efectivamente como una constante que se agrega a cada píxel. Si es demasiado alto, o incluso negativo, también puede empujar a los píxeles fuera del rango permitido.
¡Evita recortar tus datos!
Si se produce recorte, ya no sabemos qué está sucediendo en las partes más brillantes u oscuras de la imagen, lo que puede frustrar cualquier análisis posterior. Por lo tanto, durante la adquisición de imágenes, se deben ajustar todos los controles disponibles para garantizar que se evite el recorte.
Al adquirir una imagen entera sin signo de 8 bits, ¿es justo decir que sus datos están bien siempre que su valor mínimo de píxeles sea 0 y su valor máximo sea 255?
¡No! Al menos no realmente.
No puedes almacenar píxeles fuera del rango 0–255. Si tu imagen contiene píxeles con cualquiera de esos valores extremos, no puedes estar seguro de si se ha producido un recorte o no. Por lo tanto, debes asegurarte de que las imágenes que adquieras no contengan píxeles con los valores más extremos permitidos por la profundidad de bits de la imagen. Para tener la certeza de que tus datos de 8 bits no se recortan, el rango máximo sería 1–254.
La profundidad de bits de una imagen probablemente sea un múltiplo de 8, pero la profundidad de bits que un detector (por ejemplo, CCD) puede admitir podría no serlo.
Por ejemplo, ¿cuál es el valor máximo en una imagen de 16 bits adquirida utilizando una cámara con output de 12 bits?
¿Y cuál es el valor máximo en una imagen de 8 bits adquirida con una cámara con output de 14 bits?
Supongamos que en ambos casos se utilizan enteros sin signo.
El valor máximo de una imagen de 16 bits obtenida con una cámara de 12 bits es 4095 (es decir, 212-1 ).
El valor máximo de una imagen de 8 bits obtenida con una cámara de 14 bits es 255; los bits adicionales de la cámara no cambian esto. Pero si la imagen se guardara en 16 bits, el valor máximo sería 16383.
Por lo tanto, ten en cuenta que el rango real de valores posibles depende del equipo de adquisición y de la profundidad de bits de la imagen misma. Dominará la profundidad de bits más baja.
Errores de redondeo#
El redondeo es un problema más sutil que el recorte. Una vez más, es relevante desde la adquisición.
Por ejemplo, supongamos que se adquiere una imagen en la que hay 1000 niveles distintos y cuantificables de luz emitida por diferentes partes de una muestra. En una imagen de 8 bits no es posible asignarles valores de píxel diferentes, pero en una imagen de 16 o 32 bits sí que cabrían. Si nuestra imagen es de 8 bits y queremos evitar el recorte, primero tendremos que reducir la escala de los recuentos de fotones originales, con lo que los píxeles con recuentos de fotones diferentes se redondearán para que tengan los mismos valores y se perderán sus diferencias originales.
No obstante, los errores de redondeo durante la adquisición suelen ser pequeños: puede que realmente no importe si no podemos diferenciar entre detectar 1.000 fotones y 1.003 fotones.
El redondeo puede ser un problema mayor cuando se trata de operaciones de procesado como el filtrado, que a menudo implican calcular promedios sobre muchos píxeles (véase Filtros). La buena noticia es que en esta fase posterior a la adquisición podemos convertir nuestros datos a punto flotante y obtener fracciones si las necesitamos.
Errores de redondeo en punto flotante
Como revelación completa, debo admitir que el uso de tipos de punto flotante es sólo una solución parcial a los problemas de redondeo. Incluso una imagen de 64 bits en punto flotante no puede almacenar todos los valores de píxel útiles con una precisión perfecta, y números aparentemente sencillos como 0.1 sólo se representan de forma imprecisa.
Pero esto no es realmente inesperado: esta limitación binaria es similar a la forma en que no podemos escribir 1/3 en decimal con exactitud. Podemos escribir 0.3333333, pero nuestro nivel de precisión dependerá de nuestra voluntad de seguir sumando 3 después del punto decimal.
En cualquier caso, redondear 0.1 a 0.100000001490116119384765625 (una posible representación en punto flotante) no es tan malo como redondearlo a 0 (una representación entera), y las imprecisiones de los números en punto flotante en el análisis de imágenes son normalmente lo bastante pequeñas como para no tenerlas en cuenta.
Para más información, consulte https://xkcd.com/217/.
Más bits es mejor (normalmente)
Al considerar tanto el recorte como el redondeo, surge la sencilla regla de la profundidad de bits: si quieres la máxima información y precisión en tus imágenes, más bits es mejor. Esto se muestra en Figura 23.
Cuando se le da la opción de adquirir una imagen de 16 u 8 bits, la mayoría de las veces debe optar por la primera.

Figura 23 Ilustración de la precisión comparativa de (de izquierda a derecha) imágenes de 8 bits, 16 bits y 32 bits. Si una imagen de 8 bits es como crear una escultura a partir de grandes bloques de construcción, una imagen de 16 bits es más parecida a utilizar Lego y una imagen de 32 bits en punto flotante se asemeja a utilizar arcilla. Cualquier cosa que se pueda crear con los bloques también se puede hacer con el Lego; cualquier cosa que se haga con el Lego también se puede hacer con la arcilla. Esto no funciona a la inversa: algunas creaciones complejas sólo pueden representarse correctamente con arcilla, y los bloques de construcción sólo permiten, como mucho, una burda aproximación. Por otra parte, si sólo necesitas algo en bloques, no merece la pena el esfuerzo extra de Lego o la arcilla. Y, desde una distancia muy grande, puede ser difícil notar la diferencia.#
Aunque más bits es mejor es una simple regla empírica que podemos compartir con quienes no conocen las sutilezas de la profundidad de bits, no debe sostenerse con total rigor.
¿Se te ocurre alguna circunstancia en la que más bits no sean mejores?
A veces es preferible una profundidad de bits menor que una mayor:
Una mayor profundidad de bits conlleva archivos de mayor tamaño y un procesamiento potencialmente más lento. En el caso de conjuntos de datos muy grandes, esto puede suponer un problema mayor que cualquier pérdida de precisión derivada del uso de menos bits.
La cantidad de luz detectada por píxel puede ser tan baja que no se necesiten miles de valores posibles para almacenarla con precisión, y bastaría con 8 bits (o incluso menos). Para los niveles de luz en microscopía de fluorescencia biológica, ir más allá de los 16 bits rara vez aportaría algún beneficio.
Pero con conjuntos de datos pequeños para los que los costes de procesamiento y almacenamiento no son un problema, lo más seguro es errar por el lado de más bits de los que estrictamente necesitamos.

