Python: Tipos y profundidad de bits

En esta sección exploraremos cómo se representan en Python las profundidades de bits y los tipos de imagen. Veremos en particular dónde pueden salir mal las cosas al convertir entre profundidades de bits, y cómo aplicar los trucos de los capítulos anteriores para identificar problemas.

# First, our usual default imports
import sys
sys.path.append('../../../')

from helpers import *
import matplotlib.pyplot as plt
import numpy as np

Profundidad de bits y dtype

La profundidad de bits de una matriz NumPy está codificada en su tipo de datos - o su forma abreviada dtype .

ImageJ se centra en imágenes de enteros sin signo de 8 y 16 bits, así como en imágenes de punto flotante de 32 bits.

NumPy, por otro lado, ofrece una gama mucho más amplia de tipos de datos. El código para un tipo de dato Numpy no es difícil de descifrar, con uint para “unsigned integer” (“entero sin signo” en español) y float para punto flotante.

Tipo	Profundidad de bits	dtype
Entero sin signo	8	uint8
Entero con signo	8	int8
Entero sin signo	16	uint16
Entero con signo	16	int16
Entero sin signo	32	uint32
Entero con signo	32	int32
Punto flotante	32	float32
Punto flotante	64	float64

El dtype de cualquier array es fácil de comprobar:

im = load_image('sunny_cell.tif')

print(im.dtype)

uint16

Podemos imprimir algunas estadísticas básicas, como antes. En particular, podemos comprobar que los valores mínimo y máximo están dentro del intervalo esperado.

print(f'Mean: {im.mean():.2f}')
print(f'Minimum: {im.min()}')
print(f'Maximum: {im.max()}')

plt.imshow(im)
plt.show()

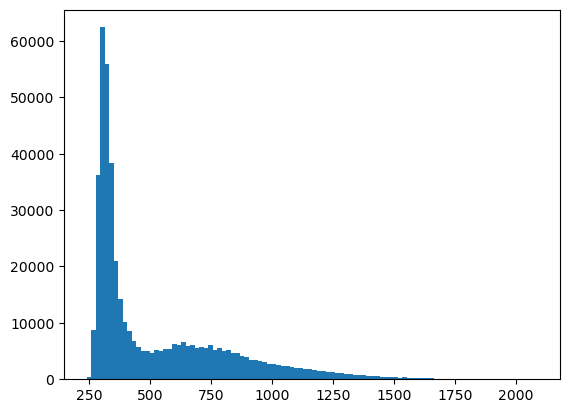
plt.hist(im.flatten(), bins=100)
plt.show()

Mean: 527.56
Minimum: 239
Maximum: 2090

Diversión con float32

Si queremos cambiar el tipo, también es fácil hacerlo.

Esto hace uso de la línea import numpy as np para darnos acceso a más propiedades y funciones de NumPy.

im_float = im.astype(np.float32)

Esto debería convertir nuestra imagen en punto flotante de 32 bits.

Sin embargo, cuando se prueba un nuevo comando siempre es una buena idea comprobar que hace lo que se esperaba. Podemos hacerlo mostrando la imagen e imprimiendo de nuevo las estadísticas.

print(f'Mean:    {im_float.mean():.2f}')
print(f'Minimum: {im_float.min()}')
print(f'Maximum: {im_float.max()}')

plt.imshow(im_float)
plt.show()

Mean:    527.56
Minimum: 239.0
Maximum: 2090.0

A mí me parece bien, pero seamos muy cuidadosos y hagamos que NumPy compruebe si los valores son realmente idénticos.

Una forma de hacerlo es con ==.

print(im == im_float)

[[ True  True  True ...  True  True  True]
 [ True  True  True ...  True  True  True]
 [ True  True  True ...  True  True  True]
 ...
 [ True  True  True ...  True  True  True]
 [ True  True  True ...  True  True  True]
 [ True  True  True ...  True  True  True]]

Hmmm, parece bastante convincente - nos da una imagen que tiene Verdadero o Falso para cada píxel. Pero debido a los límites de lo que se imprime, en realidad sólo muestra que los píxeles de las esquinas de nuestra imagen coinciden.

Si queremos asegurarnos de que todos los píxeles son iguales, podemos utilizar np.all.

print(np.all(im == im_float))

True

¡Éxito!

Pero… el escepticismo es propio de la ciencia -sobre todo del análisis de imágenes- y siempre merece la pena comprobar las cosas desde varios ángulos, por si acaso. Así que comprobemos también las estadísticas:

if im.min() == im_float.min():
    print('Minimum values are identical!')
else:
    print('Minimum values are different...')
    
if im.max() == im_float.max():
    print('Maximum values are identical!')
else:
    print('Maximum values are different...')

if im.mean() == im_float.mean():
    print('Mean values are identical!')
else:
    print('Mean values are different...')

Minimum values are identical!
Maximum values are identical!
Mean values are different...

Uh-oh… eso fue inesperado.

**De alguna manera, tenemos dos imágenes con exactamente los mismos valores de píxeles y, sin embargo, tienen un valor medio diferente.

No parece tener sentido. Tenemos que investigar imprimiendo los valores reales:

print(f'Mean values are different... {im.mean()} vs {im_float.mean()}')

Mean values are different... 527.5647778210875 vs 527.5647583007812

De acuerdo, las medias están muy muy próximas, y tenemos que ir mucho más allá del punto decimal para que haya una diferencia.

Este es un ejemplo de error de precisión.

Los errores de precisión son habituales al programar, y debemos estar siempre en guardia contra ellos. Pueden producirse en medio de los cálculos porque los resultados intermedios no se almacenan con una precisión perfecta, sino que se redondean a un valor cercano.

Esto ocurre tanto con los tipos enteros como con los de punto flotante, pero, por supuesto, es más grave cuando se trabaja con enteros. Para ilustrarlo con valores decimales (ya que para la mayoría de nosotros es más difícil pensar en binario), dividamos un número por 3 y multipliquemos el resultado por 3. Matemáticamente, deberíamos obtener el mismo resultado.

Sin embargo, si realizamos nuestros cálculos utilizando únicamente números enteros, veremos que

\[::\]

Por otro lado, si utilizamos punto flotante (con tres decimales para ilustrar) obtendríamos

\[\begin{split} \begin{align} \frac{10}{3} & \approx 3.333 \\ \\ 3.333 \times 3 & = 9.999 \end{align} \end{split}\]

Ninguno da el resultado final matemáticamente «correcto» de 10, debido a los errores de precisión.

En consecuencia, en lugar de comprobar si los valores no enteros son idénticos entre sí utilizando ==, a menudo necesitamos comprobar si están muy próximos entre sí. Para ello podemos utilizar np.allclose.

np.allclose(im.mean(), im_float.mean())

True

Hacia los 8 bits

Anteriormente, teníamos una imagen con una profundidad de bits baja y aumentamos la profundidad de bits. Esto estaba bien.

Ahora es el momento de ir en la dirección opuesta y comprobar de nuevo que funciona.

im_u8 = im.astype(np.uint8)

print(f'Mean:    {im_u8.mean():.2f}')
print(f'Minimum: {im_u8.min()}')
print(f'Maximum: {im_u8.max()}')

plt.imshow(im_u8)
plt.show()

Mean:    96.25
Minimum: 0
Maximum: 255

Oh, vaya. Esto categóricamente no está bien.

Nuestros valores mínimo y máximo están en el rango 0-255 - que es todo lo que se permite en una imagen entero sin signo de 8 bits, así que tiene sentido. Pero la apariencia no tiene mucho sentido a primera vista.

Siempre que reducimos la profundidad de bits de una imagen, sabemos que los valores de los píxeles tendrán que encajar en el nuevo rango. En el texto principal, hemos considerado dos formas de que esto ocurra: por recorte o por reescalado.

Aquí, nos encontramos con una ligera idiosincrasia de NumPy con la que realmente tenemos que tener cuidado: por defecto, no recortará ni reescalará!

Pero, ¿qué hace? En lugar de buscar en Google o rastrear los documentos de NumPy, podemos experimentar.

# Create an array from 0-1000 (in increments of 100)
a = np.arange(0, 1001, 100)
print(a.dtype)
print(a)

int64
[   0  100  200  300  400  500  600  700  800  900 1000]

# Convert to uint8 and see what happens
b = a.astype(np.uint8)
print(b.dtype)
print(b)

uint8
[  0 100 200  44 144 244  88 188  32 132 232]

# Just to make things clearer
# print the original values above and the new values below
print(np.vstack([a, b]))

[[   0  100  200  300  400  500  600  700  800  900 1000]
 [   0  100  200   44  144  244   88  188   32  132  232]]

# And, once more, lets plot lots of values against their converted-to-uint8 versions
plt.plot(np.arange(-1000, 1000), np.arange(-1000, 1000).astype(np.uint8))
plt.xlabel('Original values')
plt.ylabel('uint8 values')
plt.show()

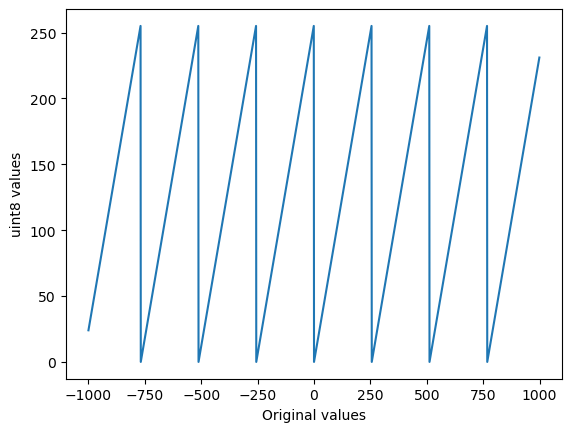
Así que parece que NumPy envuelve alrededor: al convertir 256 a uint8 se convierte en 0, 257 se convierte en 1 y así sucesivamente.

Esto significa que, para convertir una imagen a uint8, tenemos que tomar cartas en el asunto para reducir la pérdida de datos. Para empezar, vamos a recortar.

Conversión con recorte

El truco consiste en recortar la imagen antes de convertirla con astype:

im_u8_clipped = np.clip(im, 0, 255).astype(np.uint8)

print(im_u8_clipped.dtype)
print(f'Mean:    {im_u8_clipped.mean():.2f}')
print(f'Minimum: {im_u8_clipped.min()}')
print(f'Maximum: {im_u8_clipped.max()}')

plt.imshow(im_u8_clipped)
plt.show()

uint8
Mean:    255.00
Minimum: 239
Maximum: 255

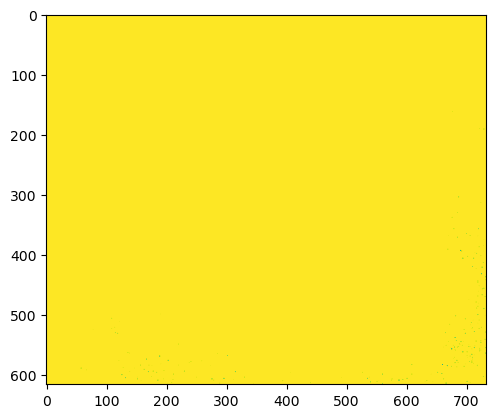
Esto ha funcionado en cierto sentido, pero no muy bien. Nuestros píxeles están en el rango 0-255, pero recordemos que en el histograma anterior casi todos los píxeles tenían originalmente un valor superior a 255. Cuando recortamos, estos píxeles se convirtieron en 255, y se perdió toda distinción.

Conversión con reescalado

Podemos calcular el valor máximo posible de un entero sin signo para una profundidad de bits específica \(N\) como \(2^{N}-1\).

Con Numpy, podemos utilizar el operador ** para esto.

max_u8 = 2**8 - 1
print(f'Maximum value for 8-bit unsigned integer: {max_u8}')

max_u16 = 2**16 - 1
print(f'Maximum value for 16-bit unsigned integer: {max_u16}')

Maximum value for 8-bit unsigned integer: 255
Maximum value for 16-bit unsigned integer: 65535

Por lo tanto, para convertir nuestra imagen de 16 bits a 8 bits mediante reescalado, podríamos multiplicar los valores de los píxeles por el cociente de estos valores máximos, es decir, por \(\frac{255}{65535} \).

im_uint8_scaled = im * (255 / 65535)
im_uint8_scaled = im_uint8_scaled.astype(np.uint8)

print(im_uint8_scaled.dtype)
print(f'Mean:    {im_uint8_scaled.mean():.2f}')
print(f'Minimum: {im_uint8_scaled.min()}')
print(f'Maximum: {im_uint8_scaled.max()}')

plt.imshow(im_uint8_scaled)
plt.show()

uint8
Mean:    1.68
Minimum: 0
Maximum: 8

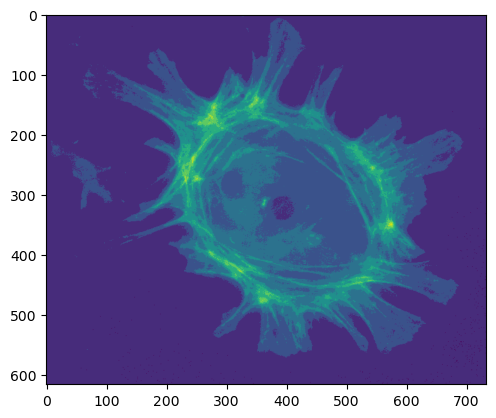
Esto ha funcionado más o menos, pero hay que tener en cuenta que el valor máximo del píxel es muy bajo. Hemos perdido mucha información: exprimiendo nuestros valores en un rango muy pequeño de enteros, mucho menos que los 256 disponibles.

Lo ideal sería reescalar la imagen conservando la mayor cantidad de información posible. Nos gustaría que los valores de nuestra imagen de salida llenaran todo el rango de 0-255.

Podemos hacerlo en cinco pasos:

1. Convertir la imagen a punto flotante (para no perder información por redondeo)

2. Restar el valor mínimo, para que el mínimo se convierta en cero

3. Dividir por el nuevo valor máximo, de forma que el máximo se convierta en uno

4. Multiplicar por 255

5. Convertir a 8 bits

im_temp = im - im.min()
im_temp = im_temp / im_temp.max()
im_temp = im_temp * 255

im_uint8_scaled = im_temp.astype(np.uint8)

print(im_uint8_scaled.dtype)
print(f'Mean:    {im_uint8_scaled.mean():.2f}')
print(f'Minimum: {im_uint8_scaled.min()}')
print(f'Maximum: {im_uint8_scaled.max()}')

plt.imshow(im_uint8_scaled)
plt.show()

uint8
Mean:    39.25
Minimum: 0
Maximum: 255

En cuanto a las conversiones a 8 bits, el reescalado parece más acertado que el simple recorte, y la salida llena toda la gama disponible.

No obstante, no olvides que las estadísticas son diferentes y que hemos cambiado los valores de los píxeles.

Por lo tanto, no es algo que debamos hacer sin una buena razón.

Resumen

**El mensaje clave aquí es que es muy fácil cambiar la profundidad de bits y el tipo de una imagen, pero también es muy fácil que las cosas salgan mal.

A veces se trata de pequeños errores de precisión. A veces son grandes errores que destruyen datos.

Pero si sabes cómo mostrar imágenes, hacer mediciones y generar histogramas, siempre puedes comprobar qué ocurre con los datos en cada paso. Esto puede ayudarte a asegurarte de que no se está perdiendo nada por el camino.