Umbral

Contenido

Umbral#

Bosquejo del capítulo

Segmentación de imágenes es el proceso de detectar objetos en una imagen.
Umbral global identifica valores de píxeles por encima o por debajo de un umbral particular
La elección del umbral puede introducir bias
Los métodos de umbral automatizados a menudo pueden determinar un buen umbral basándose en el histograma de la imagen y las estadísticas, pero solo si se cumplen algunas suposiciones.
El umbral es más poderoso cuando se combina con filtrado y resta

Introducción#

Antes de que podamos medir algo en una imagen, primero debemos detectarlo.

A veces, la “detección” puede implicar [dibujar manualmente regiones de interés (ROI)] (chap_rois). Sin embargo, este laborioso proceso no escala muy bien. También puede ser bastante subjetivo.

En este capítulo, comenzaremos a explorar formas alternativas de identificar objetos dentro de imágenes. Un “objeto” es algo que queremos detectar. Dependiendo de la aplicación, un objeto puede ser un núcleo, una célula, un vaso, una persona, un pájaro, un coche, un helicóptero… más o menos cualquier cosa que podamos encontrar en una imagen.

Este proceso de detección de objetos se llama segmentación de imágenes. Si podemos automatizar la segmentación de imágenes, esto no sólo será mucho más rápido que anotar regiones manualmente, sino que también debería dar resultados más reproducibles.

Imágenes binarias y etiquetadas#

Los objetos de imagen se representan comúnmente mediante imágenes binarias.

Cada píxel de una imagen binaria puede tener uno de dos valores. Normalmente, estos valores son 0 y 1. En algunos programas (incluido ImageJ), una imagen binaria tiene los valores 0 y 255, pero esto realmente no supone ninguna diferencia en cómo se utiliza: el punto clave para nuestros propósitos es que uno de los valores representa el primer plano (es decir, píxeles que forman parte de un objeto) y el otro valor representa el fondo.

Durante el resto de este capítulo, asumiremos que nuestras imágenes binarias usan 0 para el fondo (que se muestra en negro) y 1 para el primer plano (que se muestra en blanco).

Esto es importante: si podemos generar una imagen binaria en la que todos nuestros objetos de interés están en primer plano, podemos usar esta imagen binaria para ayudarnos a tomar medidas de esos objetos.

Una forma de hacerlo implica identificar objetos individuales en la imagen binaria etiquetando componentes conectados. Un componente conectado es en realidad solo un grupo conectado de píxeles de primer plano, que juntos representan un objeto especifico. Al etiquetar los componentes conectados, obtenemos una imagen etiquetada en la que los píxeles que pertenecen a cada objeto tienen un valor entero único. Todos los píxeles con el mismo valor pertenecen al fondo (si el valor es 0) o al mismo objeto.

Si es necesario, podemos trazar los límites de cada objeto etiquetado para crear regiones de interés (ROI), como las que se utilizan para realizar mediciones en ImageJ y otros tipos de software.

../../../_images/1c28b94af8656e367cf4657b142eb260854c6010f19bf96f8642e966d9bde1ce.png — Figura 63 Ejemplos de imagen en escala de grises (blobs.gif), binaria y etiquetada. En (C), a cada etiqueta se le ha asignado un color único para su visualización. En (D), los ROIs se generaron a partir de (C) y se superpusieron sobre (A). Es común utilizar una LUT para imágenes etiquetadas que asigna un color diferente a cada valor de píxel.#

Por ese motivo, muchos flujos de trabajo de análisis de imágenes involucran imágenes binarias a lo largo del camino. La mayor parte de este capítulo explorará la forma más común de generar una imagen binaria: umbral o thresholding.

Conectividad

Identificar múltiples objetos en una imagen binaria implica separar distintos grupos de píxeles que se consideran «conectados» entre sí y luego crear un ROI o etiqueta para cada grupo. La conectividad en este sentido se puede definir de diferentes maneras. Por ejemplo, si dos píxeles tienen el mismo valor y están inmediatamente uno al lado del otro (arriba, abajo, a la izquierda o a la derecha, o diagonalmente adyacentes), entonces se dice que están conectados en 8, porque hay 8 diferentes ubicaciones vecinas involucradas. Los píxeles están conectados en 4 si son adyacentes horizontal o verticalmente, pero no solo en diagonal.

La elección de la conectividad puede marcar una gran diferencia en la cantidad y el tamaño de los objetos encontrados, como muestra el ejemplo de la derecha (los distintos objetos se muestran en diferentes colores).

Pregunta

¿A qué crees que se refieren 6-conectividad y 26-conectividad?

Respuesta

La conectividad 6 es similar a la conectividad 4, pero en 3D. Si se consideran todas las diagonales 3D, terminamos con cada píxel teniendo 26 vecinos.

Umbral global#

La forma más sencilla de segmentar una imagen es aplicando un umbral global. Esto identifica los píxeles que están por encima o por debajo de un valor de umbral fijo, dando como resultado una imagen binaria.

El umbral global se puede considerar como una operación puntual porque la salida se basa únicamente en el valor de cada píxel, y no en su ubicación o sus vecinos. Para que funcione un umbral global, los píxeles dentro de los objetos deben tener valores más altos o más bajos que los demás píxeles. Veremos trucos de procesamiento de imágenes para superar esta limitación más adelante, pero por ahora nos centraremos en ejemplos en los que queremos detectar objetos que tienen valores que son claramente distintos del fondo, por lo que el umbral global podría funcionar.

Hacer thresholding usando histogramas#

Es posible saber mucho sobre una imagen con sólo mirar su histograma.

Tomemos el siguiente ejemplo:

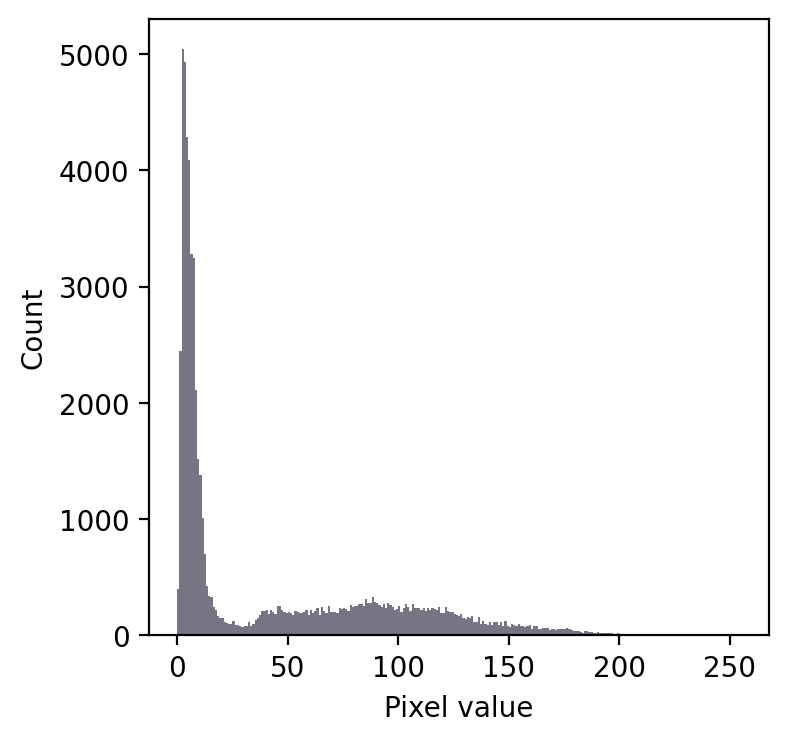
../../../_images/23220d672b35a7dce49ab4db067e63487802ea29d5eb56821dde21497c8d7cce.png

Incluso sin ver la imagen, podemos hacer algunas conjeturas sobre su contenido.

En primer lugar, hay un pico grande a la izquierda y otro mucho menos profundo a la derecha. Esto sugiere que hay al menos dos regiones distintas en la imagen. Dado que el fondo de una imagen tiende a contener muchos píxeles con valores similares, supongo que podríamos tener una imagen con un fondo oscuro.

En cualquier caso, un umbral de alrededor de 20-25 parece ser una buena opción para separar las regiones… sean cuales sean.

Si luego miramos la imagen, podemos ver que, de hecho, tenemos una imagen de fluorescencia que representa dos núcleos. Aplicando un umbral de 20 sí se consigue una buena separación de los núcleos del fondo: una segmentación exitosa.

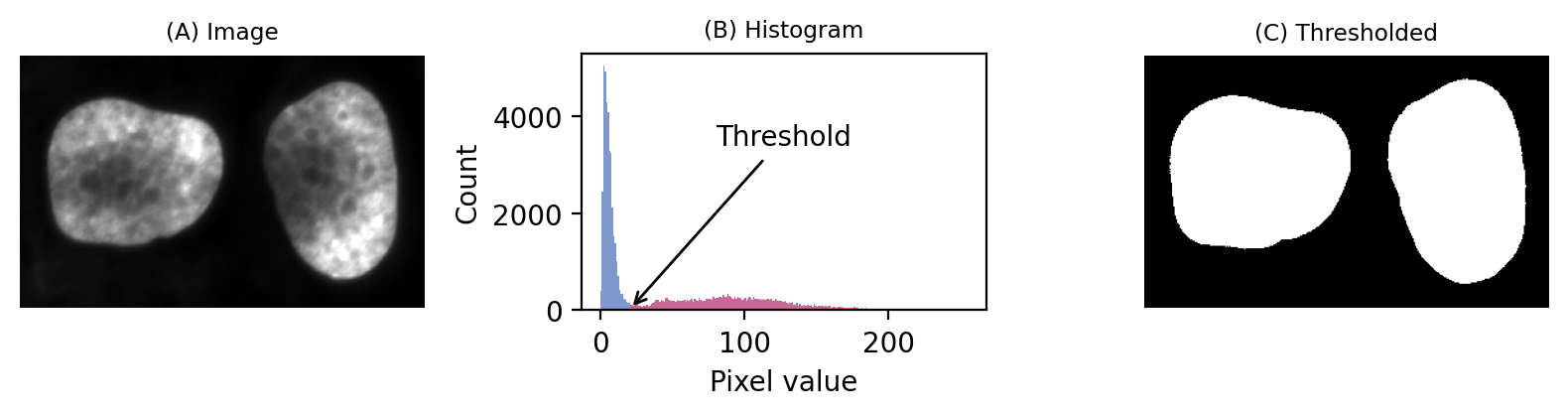
../../../_images/a428e3c74076b5d77351311d5f4d55b858e3db595cc84e7a104729137b7431fe.png — Figura 64 Una imagen de fluorescencia simple que contiene dos núcleos. Podríamos determinar un umbral potencialmente útil basándonos únicamente en mirar el histograma.#

Es cierto que se trata de un ejemplo particularmente sencillo. Deberíamos intentar uno un poco más difícil.

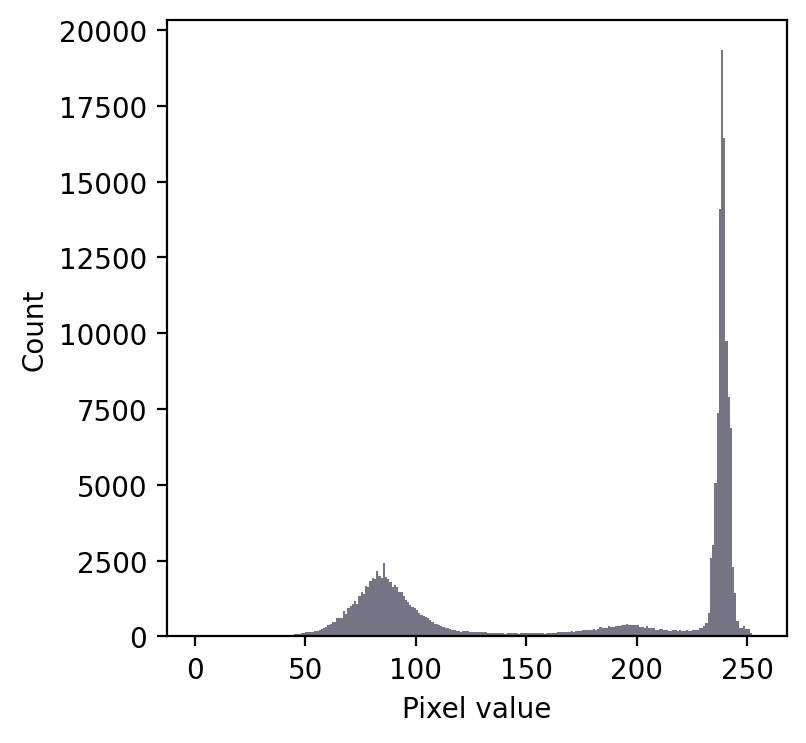
../../../_images/10a65db7100fa8bb268fc9d5336669665788686d63d66b3ae7fe7bd3b271a8b3.png

Todavía tenemos un pico grande, pero esta vez es hacia la derecha. Así que yo diría que es un fondo claro en lugar de uno oscuro.

Pero el problema es que parece que tenemos dos picos menos profundos a la izquierda. Eso sugiere al menos tres clases diferentes de píxeles en la imagen.

A partir de una inspección visual, podríamos suponer que un umbral de 140 tendría sentido. O quizás alrededor de 220. No está claro.

Esta vez, sí necesitamos mirar la imagen para decidir. Incluso entonces, no existe un umbral inequívocamente «correcto». Más bien, el que elijamos depende de si nuestro objetivo es identificar la hoja completa o sólo la región más oscura.

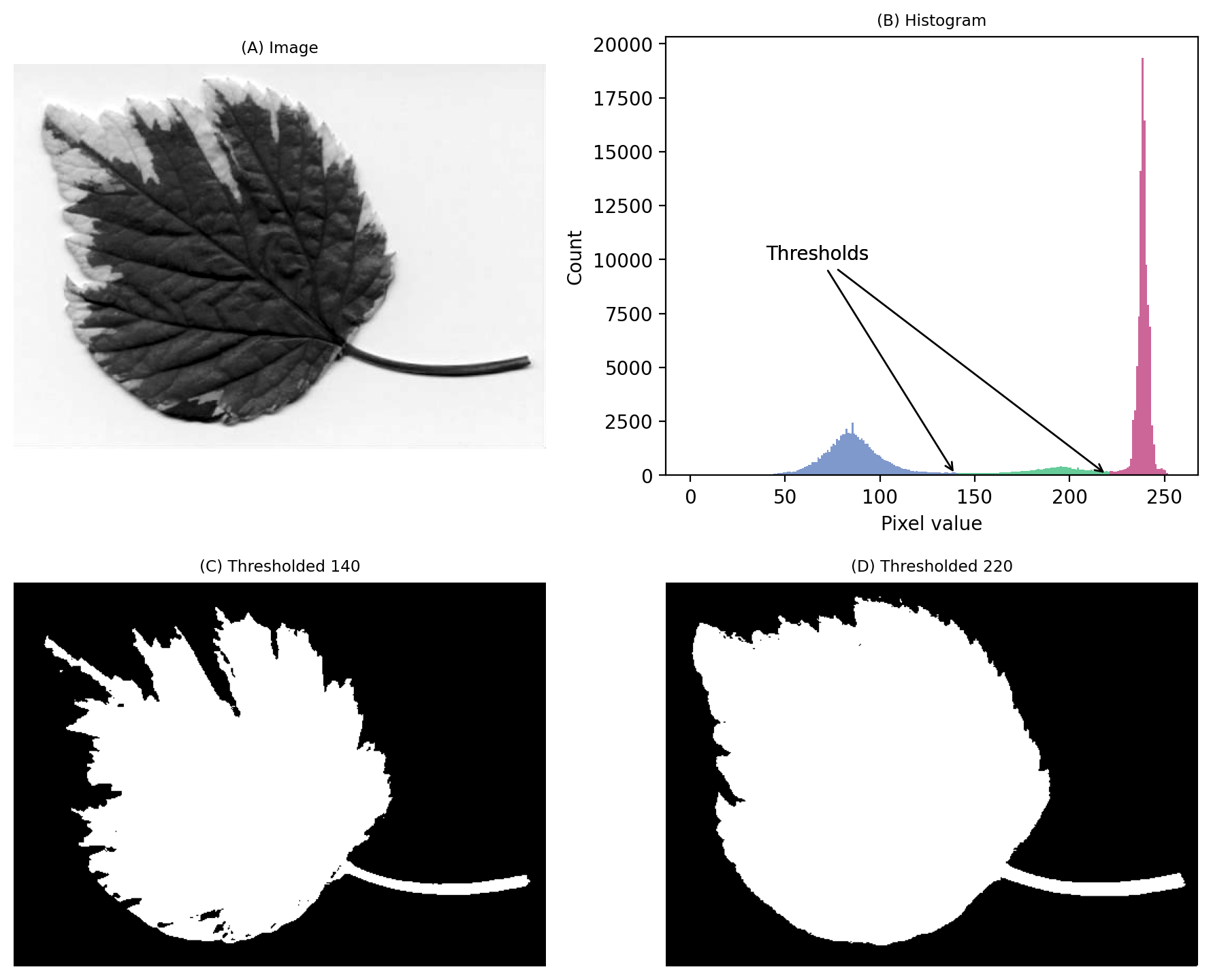
../../../_images/06399e1d6ca10359d099f5538636f7bc4c30708d519d20b716d71e0813ec772d.png — Figura 65 Una imagen donde la evaluación del histograma sugiere dos posibles umbrales. El umbral «correcto» depende del resultado deseado. Ten en cuenta que aquí identificamos píxeles *por debajo* del valor umbral, en lugar de por encima, porque el fondo es más claro.#

Los histogramas pueden ayudarnos a elegir umbrales

Los histogramas pueden ser realmente útiles a la hora de elegir valores de umbral, pero también debemos incorporar conocimiento de por qué estamos estableciendo umbrales.

La importancia de la elección del umbral#

Hemos visto que los histogramas pueden ayudarnos a identificar umbrales adecuados, pero no nos eximen de la necesidad de pensar. Esto es particularmente evidente cuando los objetos no son muy distintos. La elección exacta del umbral puede ser entonces crucial.

Figura 66 muestra un ejemplo donde el objetivo es detectar los puntos brillantes (lisosomas). Ningún umbral global puede darnos resultados perfectos, pero a primera vista muchos umbrales diferentes parecen dar resultados algo sensatos. El histograma da, en el mejor de los casos, una vaga pista de dónde puede esconderse un buen umbral.

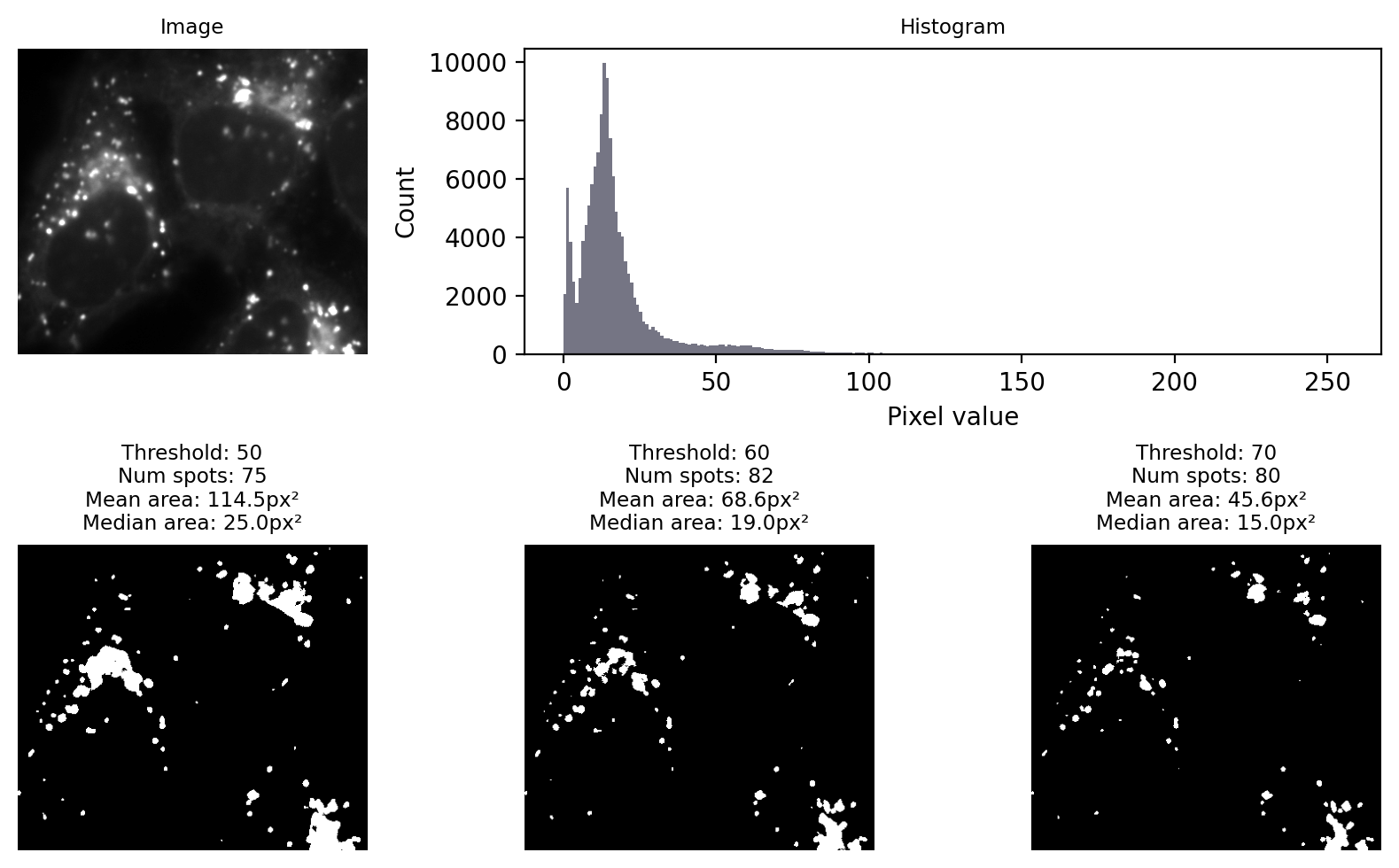
../../../_images/c50e30f0b9af9e258e0c0c889785dd4e4d643d7beca43e595170ed1bbf3e78d0.png — Figura 66 Aplicar diferentes umbrales elegidos manualmente a la misma imagen puede dar resultados bastante diferentes.#

Me gustaría transmitir tres mensajes principales de Figura 66:

La elección del umbral es crucial, ya que influye en los números y las áreas de las manchas.
- Un umbral demasiado bajo tiende a agrandar las estructuras y fusionar algunas
- Un umbral demasiado alto tiende a hacer que las estructuras sean más pequeñas y a perder algunas
Elegir un umbral manualmente brinda una gran oportunidad de introducir sesgos
Deberíamos considerar nuestros errores al seleccionar métricas de salida. Por ejemplo, si necesitáramos estimar el tamaño de una mancha a partir de cualquiera de estos resultados, entonces es probable que sea preferible la mediana, porque se ve menos afectada por manchas artificialmente grandes causadas por la fusión.

Un cuarto punto que me gustaría destacar es que la visualización también importa. Mirando sólo las imágenes binarias, es difícil evaluar realmente cualquiera de los resultados. Es de gran ayuda superponer las regiones detectadas encima de la imagen original (Figura 67). A partir de esto podemos ver mucho más claramente que ninguno de los resultados es particularmente bueno: cada umbral que probamos omite algunos puntos y fusiona otros.

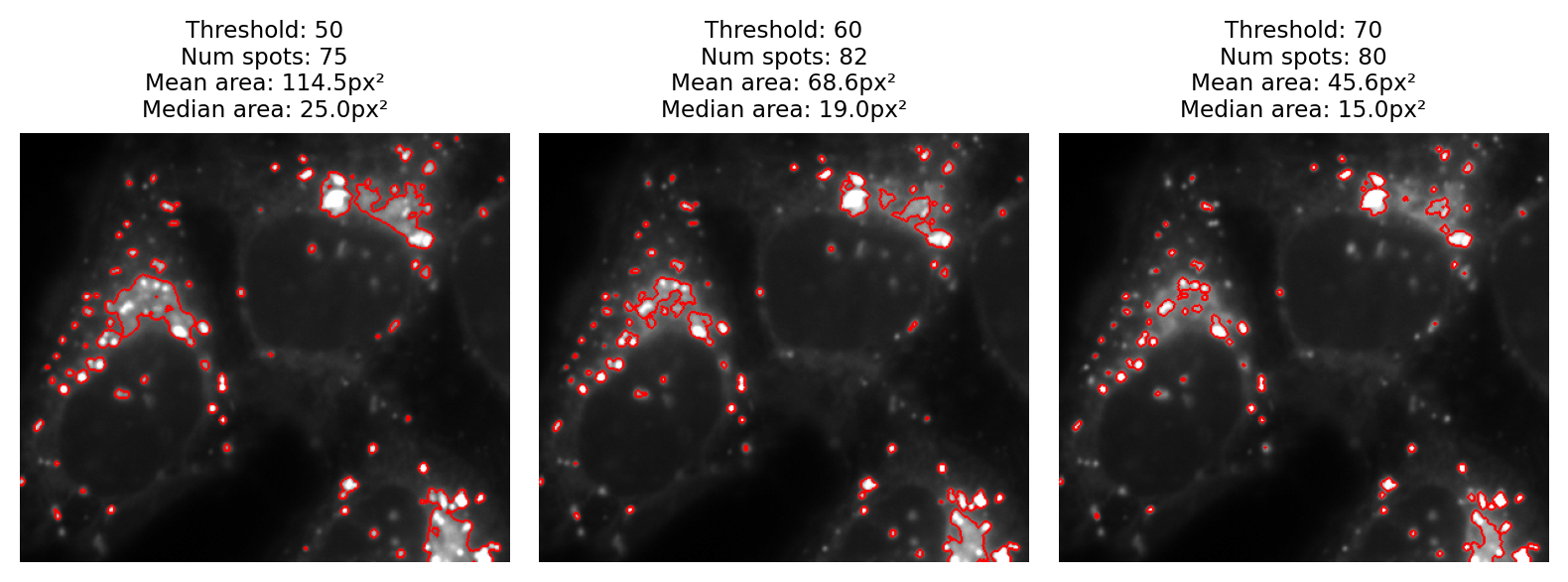
../../../_images/ed03f1ec7feebd7c8aa9332c5b020834dedfe1081014002e8ede82172e6cdaf0.png — Figura 67 Las imágenes binarias de Figura 66 se ven como superposiciones.#

¡Cuidado con las gráficas que resumen datos!

A veces me siento en reuniones de laboratorio donde la gente discute los resultados de sus análisis de imágenes sin mostrar una sola imagen. No apruebo esto en absoluto.

Es fácil generar datos resumidos con análisis de imágenes. De hecho, es inquietantemente fácil generar datos resumidos muy diferentes, incluso contradictorios, analizando las mismas imágenes de diferentes maneras. Pero lo más preocupante de todo es que a menudo se puede inventar una historia que parezca biológicamente plausible en torno a casi cualquier resultado.

Es crucial visualizar qué se detecta y mide en cada imagen, no solo una hoja de cálculo o un gráfico de los resultados. Esto es especialmente importante cuando se aplica el procesamiento por lotes a muchas imágenes a la vez. Es tentador comprobar algunas imágenes y luego confiar en la hoja de cálculo de resumen para las siguientes 10.000, pero creo que no hay sustituto para visualizar todas (o al menos una gran proporción) de las imágenes en sí.

Por esa razón, yo diría que diseñar una estrategia de visualización eficiente es tan importante como diseñar una estrategia de análisis.

Las superposiciones de imágenes suelen ser una buena manera de hacer esto: para cada imagen que analices, crea una copia RGB que describa todo lo que se detectó y midió. Idealmente, esto tendría ajustes de brillo y contraste definidos de tal manera que puedas ver de un vistazo cuando algo salió mal. Es posible que solo mires cada imagen durante una fracción de segundo a través del Explorador de Windows o el Finder de Mac, pero eso puede ser suficiente para detectar problemas que de otro modo pasarían desapercibidos.

En la última sección the last section veremos cómo aplicar pasos de pre-procesamiento a la imagen puede permitirnos reducir la proporción de puntos que se fusionan o se pierden. Pero primero consideraremos cómo automatizar la elección del umbral.

Umbrales automatizados#

No queremos elegir umbrales manualmente si podemos evitarlo, porque deja mucho espacio para el sesgo. Por otro lado, no existe una estrategia aplicable siempre para determinar un umbral automáticamente. Las imágenes varían demasiado.

Sin embargo, existen algunas técnicas ampliamente utilizadas capaces de determinar umbrales razonables para muchas imágenes basándose en el histograma. Cada uno se basa en algunas suposiciones subyacentes sobre la forma del histograma o las estadísticas de la imagen. Si se cumplen estos supuestos, el método suele funcionar bien; si no, puede funcionar bien a veces y de manera desastrosa en otras ocasiones.

En esta sección, veremos varios de los métodos de umbralización automatizados más comunes utilizando tres imágenes. Cada imagen muestra un tipo diferente de histograma que se encuentra comúnmente en las bioimágenes:

Bimodal: con dos picos distintos, correspondientes al primer plano y al fondo
Unimodal: principalmente ruido de fondo, con alguna señal interesante en un extremo
Fondo dominante: un pico de fondo grande, con una larga cola de píxeles en primer plano

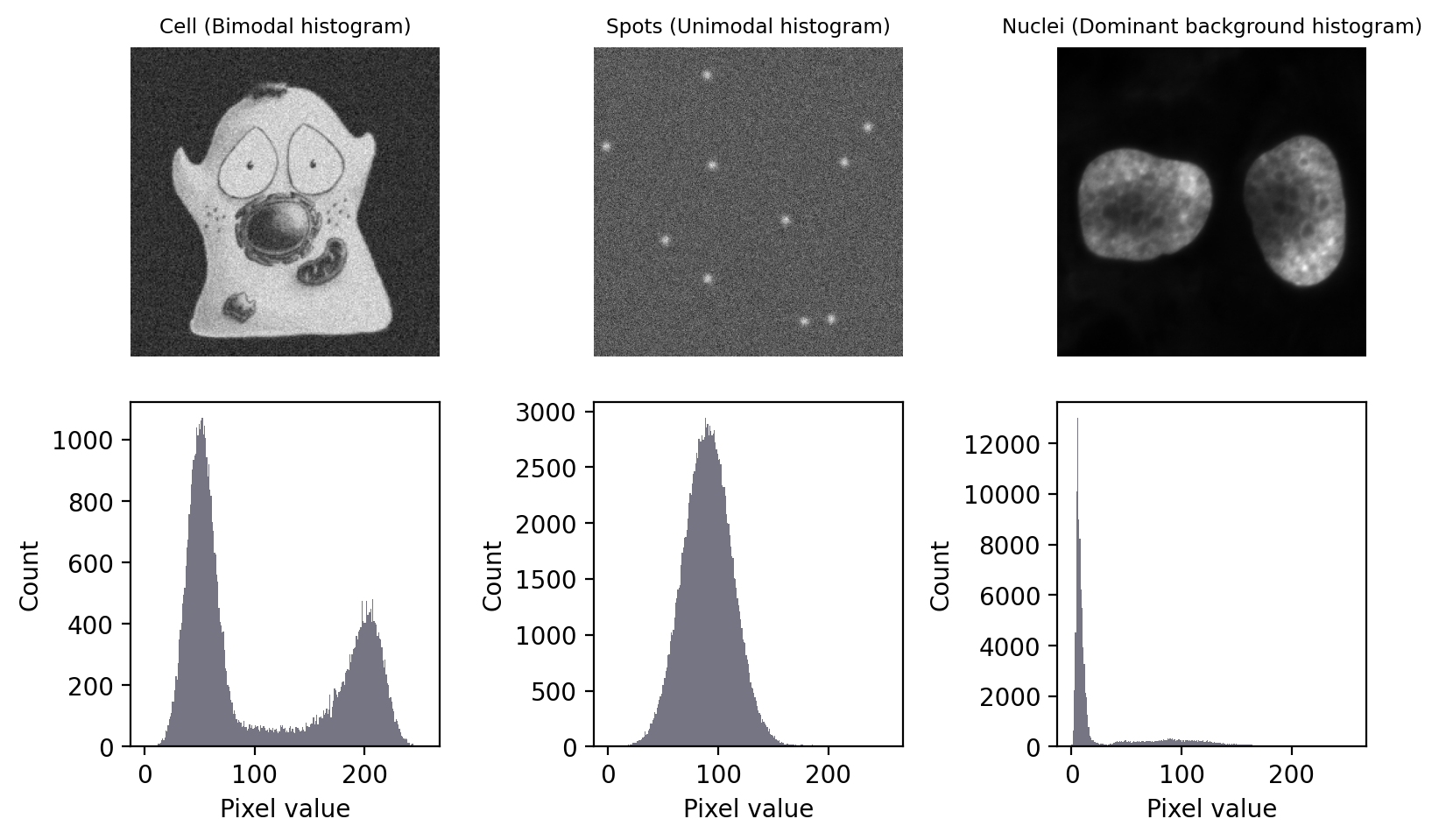
../../../_images/4c59b133e2c028a9048004551425e58597961b5bb62a480ab512ae708d27781a.png — Figura 68 Imágenes con tres tipos diferentes de histograma.#

El método de Otsu#

Por su naturaleza, el umbral global supone que hay dos clases de píxeles en la imagen (los que pertenecen a objetos interesantes y los que no) y los píxeles de cada clase tienen diferentes valores de intensidad [^fn_2]. En principio, si pudiéramos identificar los píxeles de cada una de las dos clases, podríamos calcular estadísticas como la media y la varianza (es decir, la desviación estándar al cuadrado) para ambas por separado.

El método de Otsu, introducido en 1979, se ha convertido en un método extremadamente popular para determinar un umbral. Se describe comúnmente, de manera un tanto intimidante, como “minimizar la variación de intensidad dentro de la clase”. En esencia, calcular un umbral utilizando el método de Otsu implica sumar la varianza de los píxeles de fondo a la varianza de los píxeles de primer plano, para todos los umbrales posibles. El umbral que se selecciona es aquel para el cual la suma de las varianzas es menor.

Podemos pensar en esto como intentar mantener «compactas» las distribuciones de píxeles de primer plano y de fondo: dos picos que se extienden lo menos posible.

El método de Otsu funciona muy bien con datos con un histograma bimodal, con un valle profundo en el medio. Desafortunadamente, muchas imágenes de microscopía no tienen histogramas claramente bimodales, por lo que el método puede no ser una buena opción.

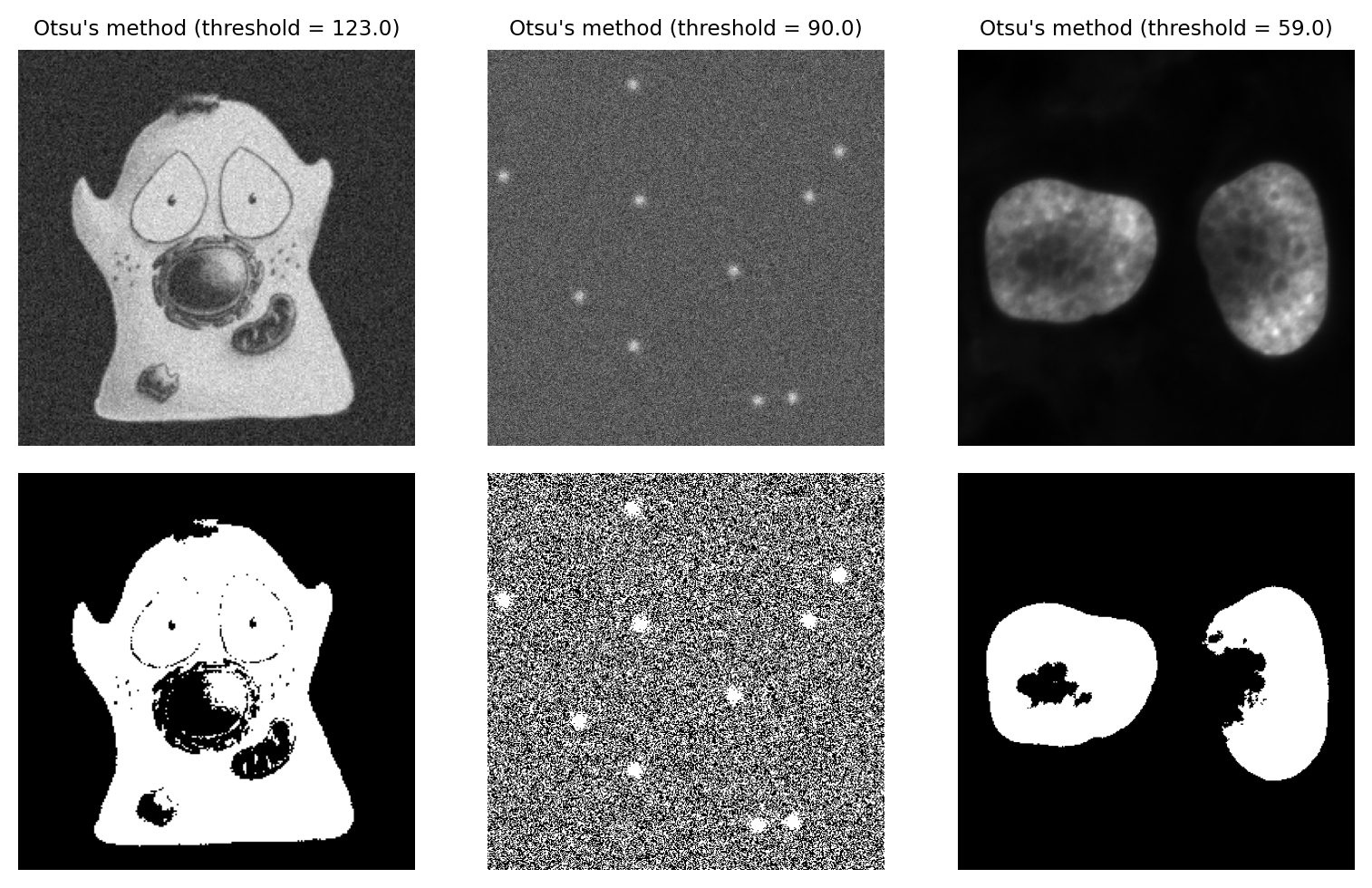
../../../_images/caa5aa14624502f9b0b1002fef074c0c0cf73ce801013fc12623d4085dc73e41.png — Figura 69 Umbral utilizando el método de Otsu. Esto funciona mejor en la imagen de la célula con un histograma bimodal. Para la imagen de puntos, no se encuentra la separación entre los picos; como resultado, aproximadamente la mitad de los píxeles se identifican como primer plano. El método también funciona bastante mal para la imagen del núcleo, a pesar de que previamente se había identificado como una imagen «más fácil» en la cual establecer umbrales.#

Método mínimo#

El método mínimo proporciona un umbral alternativo que también supone un histograma bimodal.

El punto de partida es el histograma de la imagen. Como se puede ver en Figura 68, los recuentos tienden a ser algo «ruidosos» con muchos pequeños picos espurios. El método Mínimo opera suavizando el histograma, reemplazando cada valor de conteo con el promedio de sí mismo y los conteos vecinos. Al repetir este proceso, eventualmente los picos espurios se eliminan hasta que (con suerte) queden exactamente dos picos. El umbral es entonces la ubicación del punto más profundo del valle entre esos picos.

El resultado de este proceso se ilustra en Figura 70.

Show code cell content Hide code cell content

def plot_minimum_threshold(im, bins, thresh, pos=None, max_iters=100):
    if pos:
        plt.subplot(pos)

    def find_local_maxima_idx(hist):
        # This code is taken from scikit-image because it is not publicly accessible
        # https://github.com/scikit-image/scikit-image/blob/v0.19.0/skimage/filters/thresholding.py#L821

        # We can't use scipy.signal.argrelmax
        # as it fails on plateaus
        maximum_idxs = list()
        direction = 1

        for i in range(hist.shape[0] - 1):
            if direction > 0:
                if hist[i + 1] < hist[i]:
                    direction = -1
                    maximum_idxs.append(i)
            else:
                if hist[i + 1] > hist[i]:
                    direction = 1

        return maximum_idxs

    # Create a histogram with bin centers
    hist, bin_edges = np.histogram(im.ravel(), bins=bins)
    hist = hist.astype(np.float64)
    centers = (bin_edges[1:] + bin_edges[:-1])/2.0
    smooth_hist = hist.copy()

    # Smooth histogram until there are <=2 peaks
    for ii in range(max_iters):
        smooth_hist = ndimage.uniform_filter1d(smooth_hist, 3)
        max_inds = find_local_maxima_idx(smooth_hist)
        if len(max_inds) < 3:
            break

    # Check this worked
    if len(max_inds) != 2:
        raise RuntimeError('Unable to find 2 maxima in smoothed histogram!')

    plt.hist(centers, bins=len(hist), weights=hist, color=(0.1, 0.1, 0.2, 0.1))
    plt.hist(centers, bins=len(smooth_hist), weights=smooth_hist, color=(0.6, 0.2, 0.2, 0.4))
    plt.plot(centers[max_inds], smooth_hist[max_inds], color=(0.2, 0.2, 0.6, 0.4))
    plt.plot(centers[thresh], smooth_hist[thresh], marker='.')



from skimage.filters import threshold_minimum

im_cell, im_spots, im_nuclei = create_threshold_images()

fig = create_figure(figsize=(8, 7.5))
thresh_cell = threshold_minimum(im_cell)
show_image(im_cell, title=f"Minimum method (threshold = {thresh_cell:.1f})", pos=331)
show_image(im_cell > thresh_cell, pos=334)
plot_minimum_threshold(im_cell, bins=np.arange(256), thresh=thresh_cell, pos=337)

thresh_spots = threshold_minimum(im_spots)
show_image(im_spots, title=f"Minimum method (threshold = {thresh_spots:.1f})", pos=332)
show_image(im_spots > thresh_spots, pos=335)
plot_minimum_threshold(im_spots, bins=np.arange(256), thresh=thresh_spots, pos=338)

thresh_nuclei = threshold_minimum(im_nuclei)
show_image(im_nuclei, title=f"Minimum method (threshold = {thresh_nuclei:.1f})", pos=333)
show_image(im_nuclei > thresh_nuclei, pos=336)
plot_minimum_threshold(im_nuclei, bins=np.arange(256), thresh=thresh_nuclei, pos=339)

plt.tight_layout()
glue_fig('fig_thresholds_method_minimum', fig)

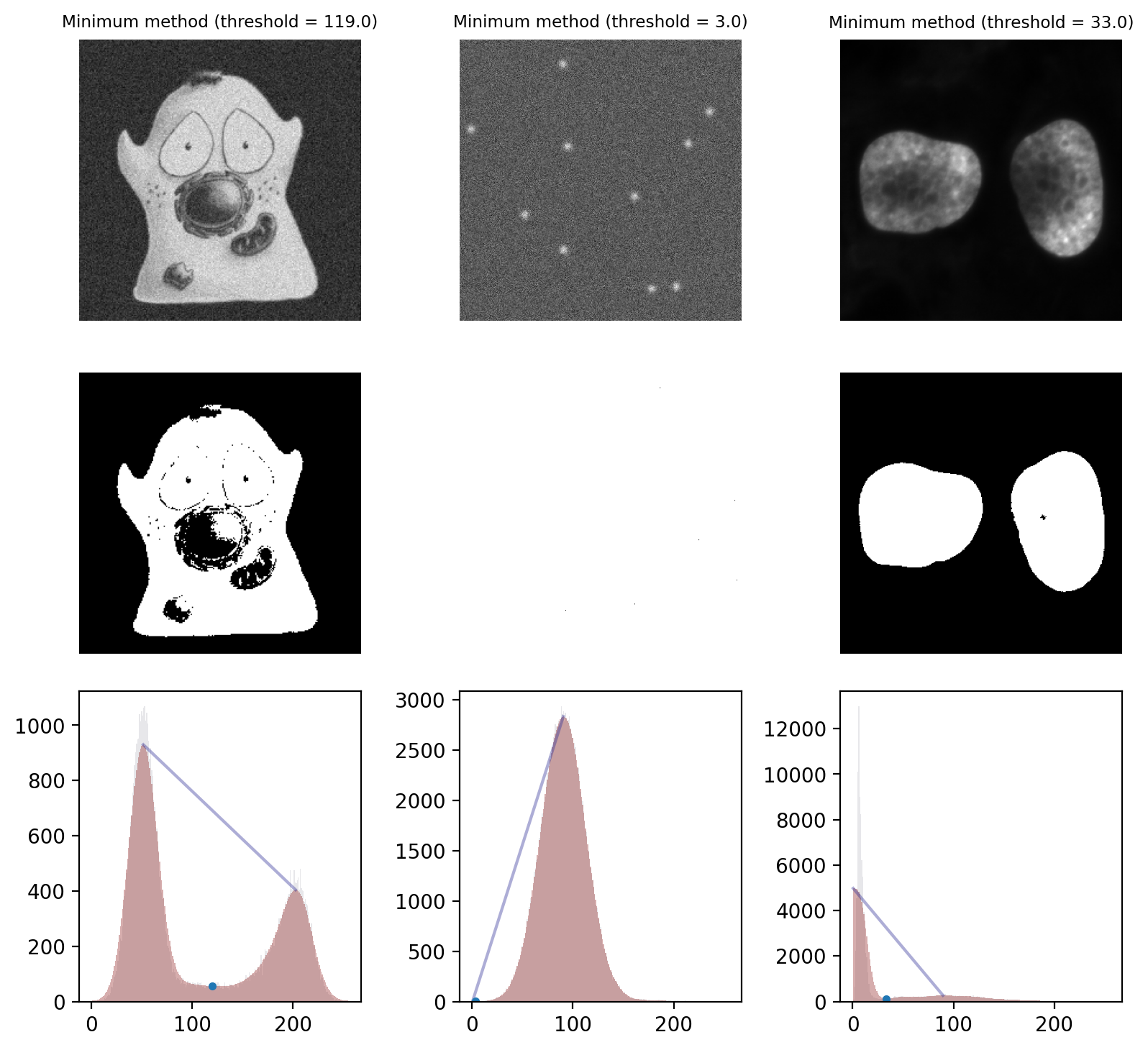
../../../_images/6dd8e1e2e68b37c01dc83650fdcbf9b4bfe1c3f75e0357037d198d9e3066a7c5.png — Figura 70 Umbral utilizando el método Mínimo. Los histogramas suavizados utilizados en el cálculo se muestran en rojo, y los histogramas originales se muestran (débilmente) en gris. También se incluye una línea que conecta los dos picos finales y el umbral marcado con un punto.
Esto funciona bien en la imagen de las células y bastante bien en la imagen de los núcleos. Sin embargo, falla mucho en la imagen de los puntos, donde casi todo se detecta en primer plano. Este es un caso en el que el método converge (debido a que la imagen es ruidosa y, por lo tanto, tiene muchos picos pequeños en el histograma), aunque preferiríamos que no fuera así.#

Una “característica” del método Mínimo es que no se garantiza que converja. Es muy posible que ninguna cantidad de suavizado dé como resultado un histograma con 2 picos: tal vez solo haya 1 pico, o ninguno en absoluto si todos los píxeles son solo un valor constante.

Esto podría ser potencialmente una ventaja: puede ser mejor no devolver ningún umbral que devolver uno realmente malo. Sin embargo, en la mayoría de las imágenes reales no podemos contar con que el método no converja: a menudo converge, incluso si no necesariamente converge a ningún valor deseable.

Método del triángulo#

El “método del triángulo” es un enfoque popular para determinar un umbral que funciona particularmente bien en imágenes donde hay un pico de fondo dominante, y el umbral ideal debería estar en la base de ese pico.

La idea general es que se dibuja una línea desde el pico del histograma hasta el último contenedor que contiene píxeles. Luego se traza una línea perpendicular al histograma y se maximiza la distancia al histograma. La dirección de la línea depende de si el pico está hacia la izquierda o hacia la derecha del histograma; Se ignoran todos los recuentos del otro lado.

El ancho y el alto del histograma están normalizados para abordar el hecho de que los valores de píxeles y los recuentos de intensidad están en unidades completamente diferentes y, por lo tanto, en escalas completamente diferentes.

La explicación es confusa, pero esperamos que Figura 71 la represente más claramente y proporcione una intuición de cuándo y por qué podría ser apropiado.

Show code cell content Hide code cell content

from skimage.filters import threshold_triangle

im_cell, im_spots, im_nuclei = create_threshold_images()

bins = np.arange(0, 256)

def plot_triangle_threshold(im, bins, thresh, pos=None):
    if pos:
        plt.subplot(pos)

    # Create a histogram, identify peak and normalize counts between 0 and 1
    # Note: here we assume the peak is always to the left and we threshold to the right!
    # The proper triangle threshold flips sometimes
    hist, bin_edges = np.histogram(im.ravel(), bins=bins)
    peak_ind = np.argmax(hist)
    peak_height = hist[peak_ind]
    hist = hist / peak_height

    # Identify bin centers
    # Find last bin with non-zero count
    centers = (bin_edges[1:] + bin_edges[:-1])/2.0
    ind_low, ind_high = np.where(hist > 0)[0][[0, -1]]    

    # Shift bin centers according to peak (simplified plotting)
    centers = centers - centers[peak_ind]

    # Compute 'width' of the triangle (base length)
    # Normalize centers so width becomes 1
    width = (centers[ind_high] - centers[peak_ind])
    centers = centers / width

    # Plot histogram with new values
    plt.hist(centers, bins=len(hist), weights=hist, color=(0.1, 0.1, 0.2, 0.6))

    # Plot from peak to base
    x1 = centers[peak_ind]
    y1 = hist[peak_ind]
    x2 = centers[-1]
    y2 = hist[-1]
    plt.plot([x1, x2], [y1, y2])

    # Plot from threshold to peak line
    x3 = centers[int(thresh)]
    y3 = hist[int(thresh)]
    n = np.sqrt((y2 - y1)**2 + (x2 - x1)**2)
    x4 = (y2 - y1) / n
    y4 = -(x2 - x1) / n
    # Find intersection
    # Thank you, wikipedia
    # https://en.wikipedia.org/wiki/Line–line_intersection#Given_two_points_on_each_line
    D = (x1 - x2)*(y3 - y4) - (y1 - y2)*(x3 - x4)
    px = ((x1*y2 - y1*x2)*(x3 - x4) - (x1 - x2)*(x3*y4 - y3*x4))/D
    py = ((x1*y2 - y1*x2)*(y3 - y4) - (y1 - y2)*(x3*y4 - y3*x4))/D
    plt.plot([x3, px], [y3, py])

    # Setup display
    plt.xlim([0, 1])
    plt.ylim([0, 1])
    plt.xticks([0, 0.5, 1.0])
    plt.yticks([0, 0.5, 1.0])
    plt.gca().set_aspect('equal')


fig = create_figure(figsize=(8, 7))
thresh_cell = threshold_triangle(im_cell)

show_image(im_cell, title=f"Triangle method (threshold = {thresh_cell:.1f})", pos=331)
show_image(im_cell > thresh_cell, pos=334)
plot_triangle_threshold(im_cell, bins=bins, thresh=thresh_cell, pos=337)

thresh_spots = threshold_triangle(im_spots)
show_image(im_spots, title=f"Triangle method (threshold = {thresh_spots:.1f})", pos=332)
show_image(im_spots > thresh_spots, pos=335)
plot_triangle_threshold(im_spots, bins=bins, thresh=thresh_spots, pos=338)

thresh_nuclei = threshold_triangle(im_nuclei)
show_image(im_nuclei, title=f"Triangle method (threshold = {thresh_nuclei:.1f})", pos=333)
show_image(im_nuclei > thresh_nuclei, pos=336)
plot_triangle_threshold(im_nuclei, bins=bins, thresh=thresh_nuclei, pos=339)

plt.tight_layout()
glue_fig('fig_thresholds_method_triangle', fig)

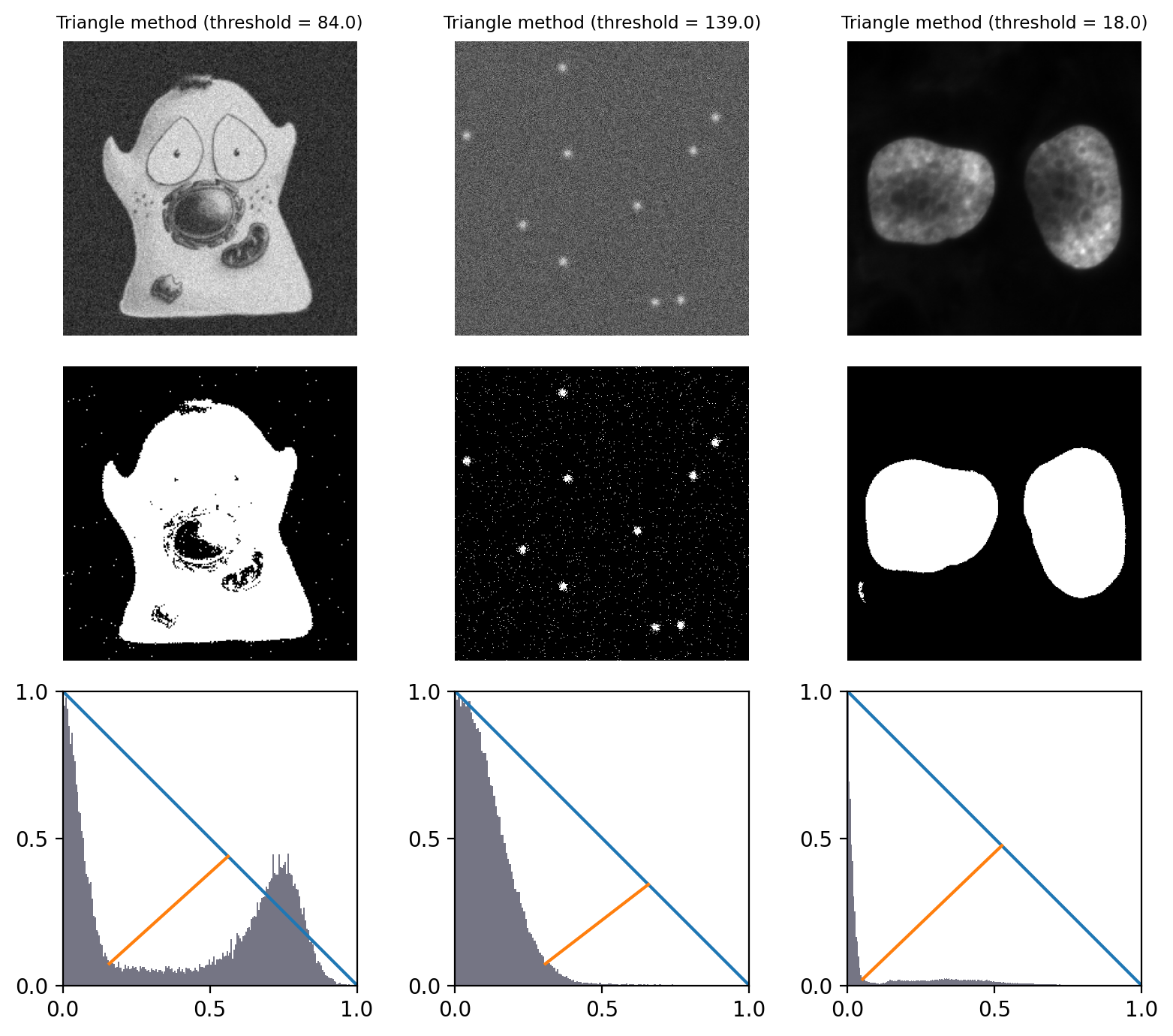
../../../_images/088552f367c7ec47da3c00e4967ea7e67d79fff75f25a5f1107dce3ecf1e31b3.png — Figura 71 Umbralización mediante el método del Triángulo. Debido a que todos los histogramas de ejemplo tienen un pico dominante, este funciona bastante bien en todos los casos, aunque tiende a detectar más píxeles de primer plano en la imagen de la célula que otros métodos (porque el umbral está en la base del pico en lugar de entre los dos modos). .
Los histogramas representan los triángulos que dan nombre al método. Se han normalizado y truncado para incluir sólo la parte relevante.#

Método de promedio#

Un enfoque alternativo simple es omitir el histograma por completo y simplemente usar la media de todos los valores de píxeles.

En realidad, esto puede dar muy buenas razones en muchas imágenes del mundo real, aunque esto puede deberse más a la suerte que al diseño. No es un método que yo suelo utilizar.

../../../_images/43f9b3bb995eb2c42a159ee1dc1ea6e4c3c819f20d4d1469b31e4ff0a649e1d4.png — Figura 72 Umbral utilizando el método del promedio o media.#

Media y desviación estándar#

Podemos agregar un poco más al método de la media incorporando la desviación estándar, escalada por una constante. El umbral se convierte en media + k x desviación estándar, donde podemos ajustar k en función de nuestra actitud hacia la sensibilidad frente a la especificidad.

La principal ventaja de este enfoque es que no debería fallar catastróficamente en casos en los que tengamos una imagen que sea principalmente ruido (suponiendo que k sea lo suficientemente grande), a diferencia de los métodos que requieren un histograma bimodal. Sin embargo, la desventaja es que no es robusto: el umbral puede aumentar o disminuir debido a valores atípicos o a valores de primer plano que son muy diferentes de los valores de fondo.

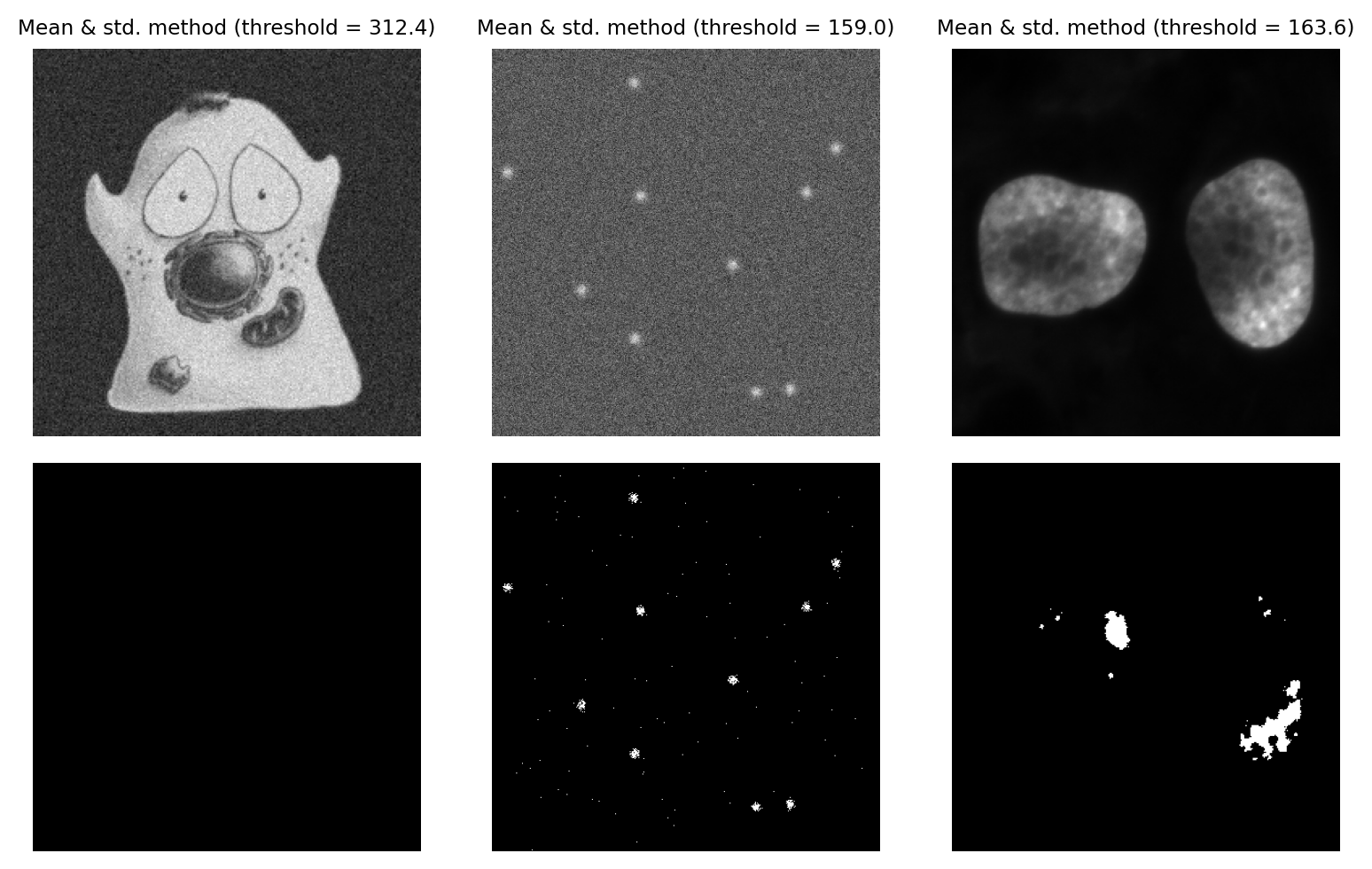
../../../_images/8eea3eb840c9046547f267e79b945ae8d332511078057c46bbeb10ca70f791de.png — Figura 73 Umbral utilizando la media + k x std.dev. método, con k = 3.#

Mediana y desviación absoluta mediana#

Una alternativa más sólida al uso de la media y la desviación estándar es utilizar la mediana y la desviación absoluta de la mediana (MAD) para determinar un umbral.

Si se ordenaran los valores de píxeles de una imagen, la mediana es el valor que estaría en el medio. El MAD se calcula de la siguiente manera:

Resta la mediana de todos los píxeles
Calcula el valor absoluto del resultado de (1) (es decir, invierte el signo de los valores negativos, para que todos sean positivos)
Calcula la mediana del resultado de (2)

Una propiedad intrigantemente útil de la MAD es que se puede escalar en 1,482 para parecerse a una desviación estándar (más robusta). El artículo de Wikipedia explica esto con más detalle.

Normalmente, usaríamos la mediana + k x MAD x 1.482, donde podemos ajustar k como si se usara para escalar una desviación estándar. Esto es útil porque las desviaciones estándar son más fáciles de ajustar para (la mayoría de) nosotros.

Usar el MAD para definir un umbral sigue siendo bastante poco común, pero personalmente me gusta mucho el método cuando trabajo con imágenes de fluorescencia muy ruidosas. Los tres requisitos principales para que este método funcione son:

La mayor parte de la imagen debe ser de fondo y ruidosa (un fondo completamente constante dará un MAD de 0 y un umbral incorrecto)
El ruido debe (más o menos) seguir una distribución normal.
La imagen no debe ser demasiado grande, porque calcular exactamente la mediana es lento.

El último punto no siempre es un problema: podemos calcular la mediana mucho más rápidamente si usamos un histograma, aunque podemos perder algo de precisión debido al binning necesario al construir el histograma.

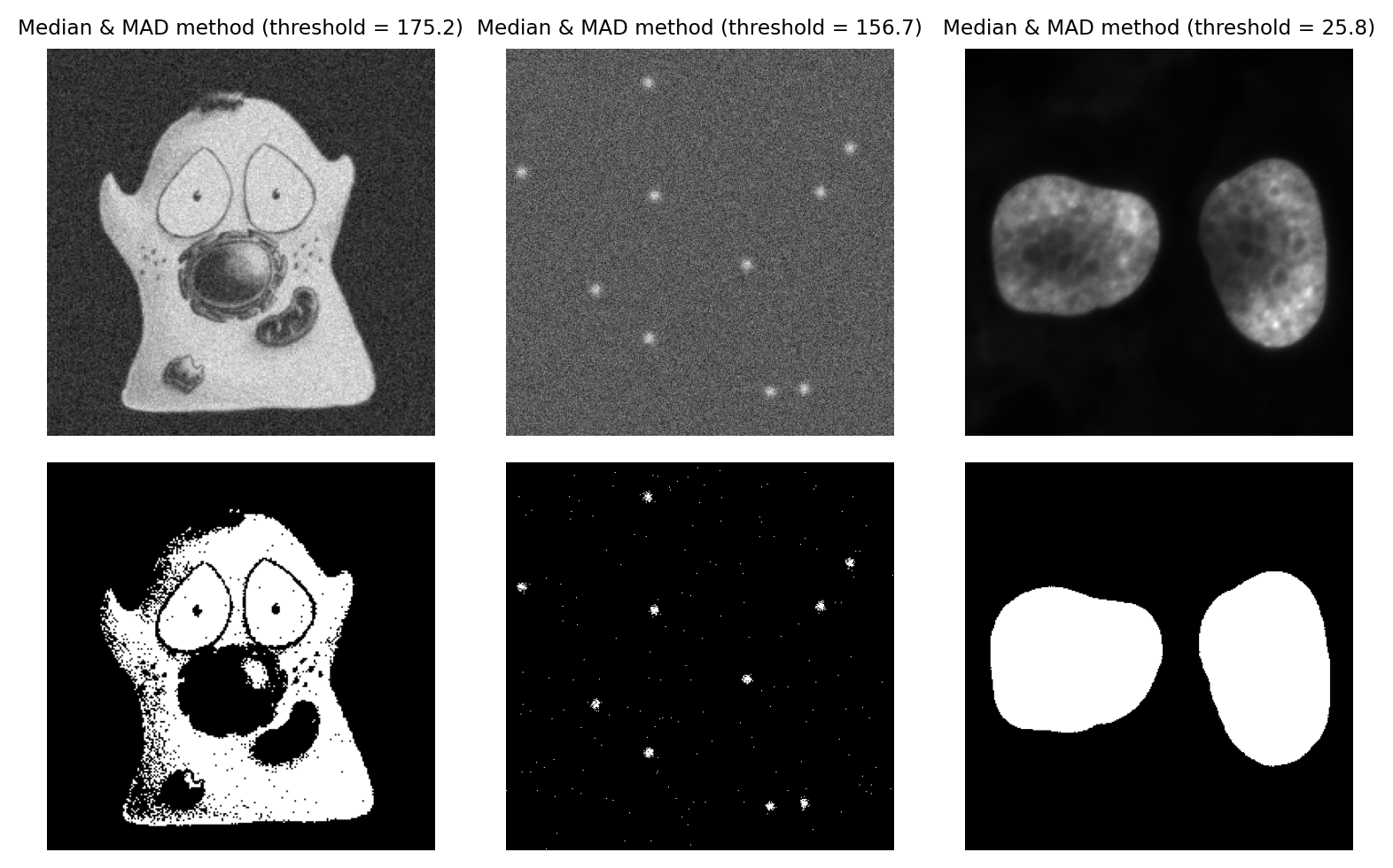
../../../_images/3a2b3b46788c14a3dab3e23de1283a965da4eb6937d3de6a4e5eca75965b9945.png — Figura 74 Umbral mediante el método MAD, con *k = 3*. Este es un fuerte candidato a ser mi método preferido para la imagen de “manchas”, porque es efectivo cuando se buscan pequeñas señales enterradas en ruido.#

El recorte (clipping) confunde los umbrales automatizados

Si los datos están [recortados] (chap_bit_depths), entonces cambian las estadísticas de los valores de píxeles y la forma del histograma de la imagen. Esto significa que la teoría que subyace a por qué debería funcionar un umbral automatizado bien podría ya no aplicar.

¡Esta es otra razón por la que siempre se debe evitar el recorte!

¿Los umbrales automatizados están menos sesgados?

A veces veo justificado el uso de métodos de umbralización automatizados porque son “menos sesgados que los umbrales manuales”.

No estoy convencido.

Estoy de acuerdo en que los umbrales automatizados son muy preferibles a elegir subjetivamente un umbral a simple vista, pero solo si se puede demostrar que funcionan de manera confiable para un conjunto de datos en particular. Un umbral automatizado incorrecto puede introducir fácilmente un sesgo sistemático que es mucho peor que establecer manualmente un umbral para cada imagen.

Estableciendo umbrales en datos difíciles#

Aplicar umbrales globales está muy bien en imágenes sencillas para las que existe claramente un umbral, pero en la práctica las cosas rara vez son tan sencillas y, a menudo, ningún umbral, manual o automático, produce resultados utilizables. Esta sección anticipa temas del próximo capítulo sobre filtros al mostrar que, con algo de procesamiento adicional, el umbral se puede rescatar incluso si inicialmente parece funcionar mal.

Encontrando el umbral en datos ruidosos#

El ruido es un problema que afecta los umbrales, especialmente en las imágenes de células vivas.

La mitad superior de Figura 75 reproduce los núcleos de Figura 64 pero con ruido adicional agregado, simulando condiciones de imagen sub-optimas. Aunque los núcleos todavía son claramente visibles en la imagen (A), las dos clases de píxeles (que antes eran fáciles de separar) ahora se han fusionado en el histograma (B). El método del umbral triangular, que había funcionado bien antes, ahora da resultados menos atractivos (C), porque el ruido ha provocado que los rangos de píxeles del fondo y del núcleo se superpongan.

Sin embargo, si aplicamos un filtro Gaussiano para suavizar la imagen, gran parte del ruido aleatorio se reduce (consulte Filtros). Esto da como resultado un histograma dramáticamente más similar al de la imagen original, (casi) libre de ruido, y el umbral nuevamente es bastante exitoso (F).

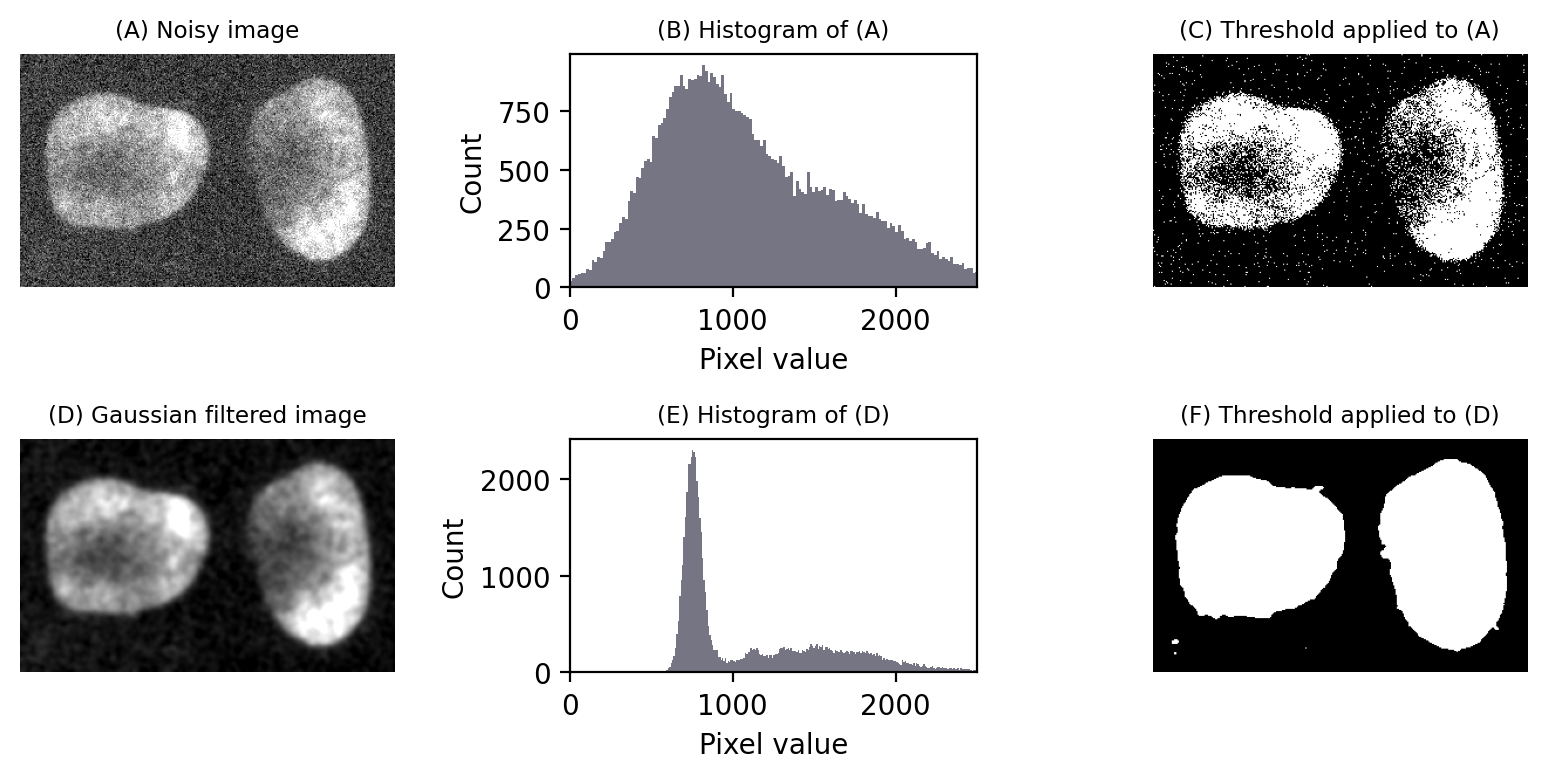
../../../_images/3c1870ac55276e7056b3a52c894786940b2df7906dd4f243b88b93ec8d919e89.png — Figura 75 El ruido puede afectar el umbral. Después de agregar ruido simulado a la imagen en Figura 64, la distinción entre píxeles con y sin núcleos es mucho más difícil de identificar en el histograma (B). Cualquier umbral daría como resultado una gran cantidad de píxeles identificados incorrectamente. Sin embargo, aplicar un filtro Gaussiano (aquí, \(\sigma = 2\)) para reducir el ruido puede mejorar drásticamente la situación (E). Los umbrales en (C) y (F) se calcularon utilizando el método del triángulo.#

Umbral local#

Otro problema común es que las estructuras que deberían detectarse aparecen sobre un fondo que a su vez varía en brillo. Esta fue la razón por la que ningún umbral funcionó muy bien en Figura 66.

Idealmente, nos gustaría aplicar un umbral que varíe en relación con el entorno local.

Hay una variedad de métodos de umbral local disponibles, muchos de los cuales son variaciones del método Niblack. Esto calcula la media y la desviación estándar de los píxeles en una ventana local alrededor de cada píxel, por ejemplo, un cuadrado de 25 x 25 píxeles.

Luego se genera un umbral separado para cada píxel, definido como local_mean - k x local_std.dev. Ten en cuenta el signo: se utiliza -k porque la definición original se centró en reconocer texto oscuro sobre un fondo claro, pero k en sí mismo puede ser un número negativo si es necesario.

Se muestra un ejemplo en Figura 76.

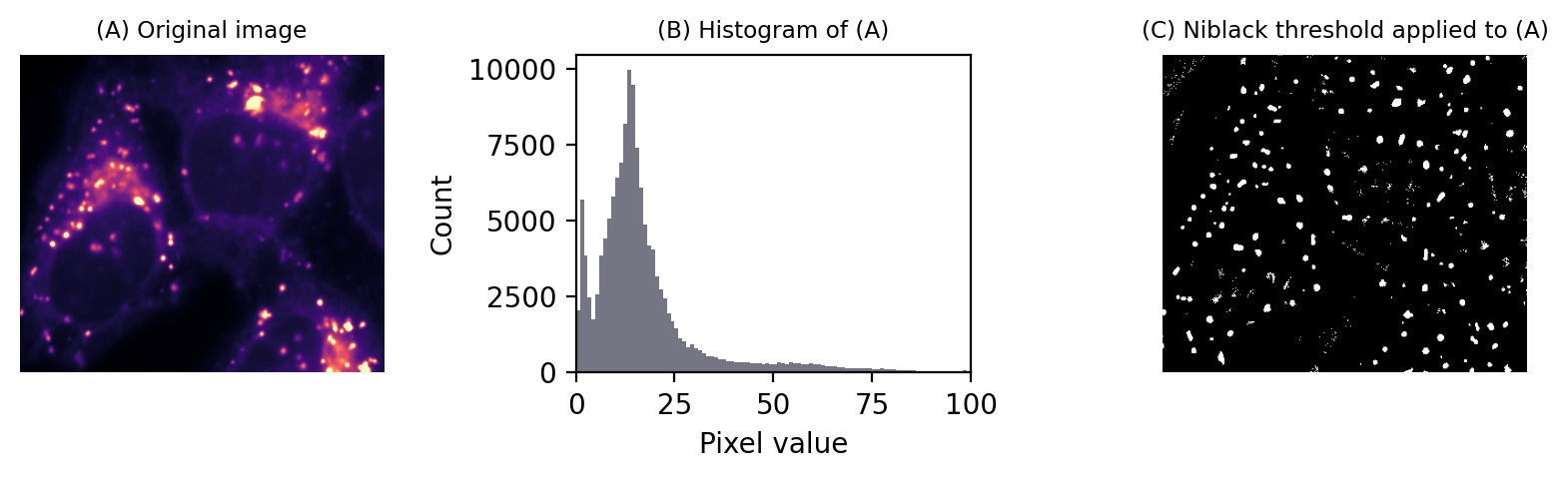
../../../_images/f59f8b117c7435a960b5b6a3faf47159a68754f01b922ad6bad72d8d48fdae6d.png — Figura 76 Umbral local para detectar manchas utilizando el método de Niblack.#

Para ser honesto, no suelo utilizar este enfoque para bioimágenes. Me parece que el tamaño de la ventana y los parámetros k son difíciles de ajustar, y sufre el problema de que la media y la desviación estándar no son robustas.

Sin embargo, el establecimiento de umbrales locales se vuelve más interesante y poderoso si tomamos el asunto en nuestras propias manos y pensamos en el problema desde un ángulo ligeramente diferente.

Supongamos que tenemos una segunda imagen que contiene valores iguales a los umbrales que queremos aplicar en cada píxel. Si simplemente restamos esta segunda imagen de la primera, podemos aplicar un umbral global de 0 para detectar lo que queremos.

Alternativamente, podríamos restar una imagen con valores que no sean exactamente iguales a los umbrales locales, pero que sean lo suficientemente similares como para aplanar efectivamente el fondo y poder aplicar un umbral global. Esto luego nos proporciona acceso a todos los métodos globales de umbralización automatizada y una intuición de cómo deben verse los histogramas para que los métodos sean apropiados. Figura 77 muestra esto en acción.

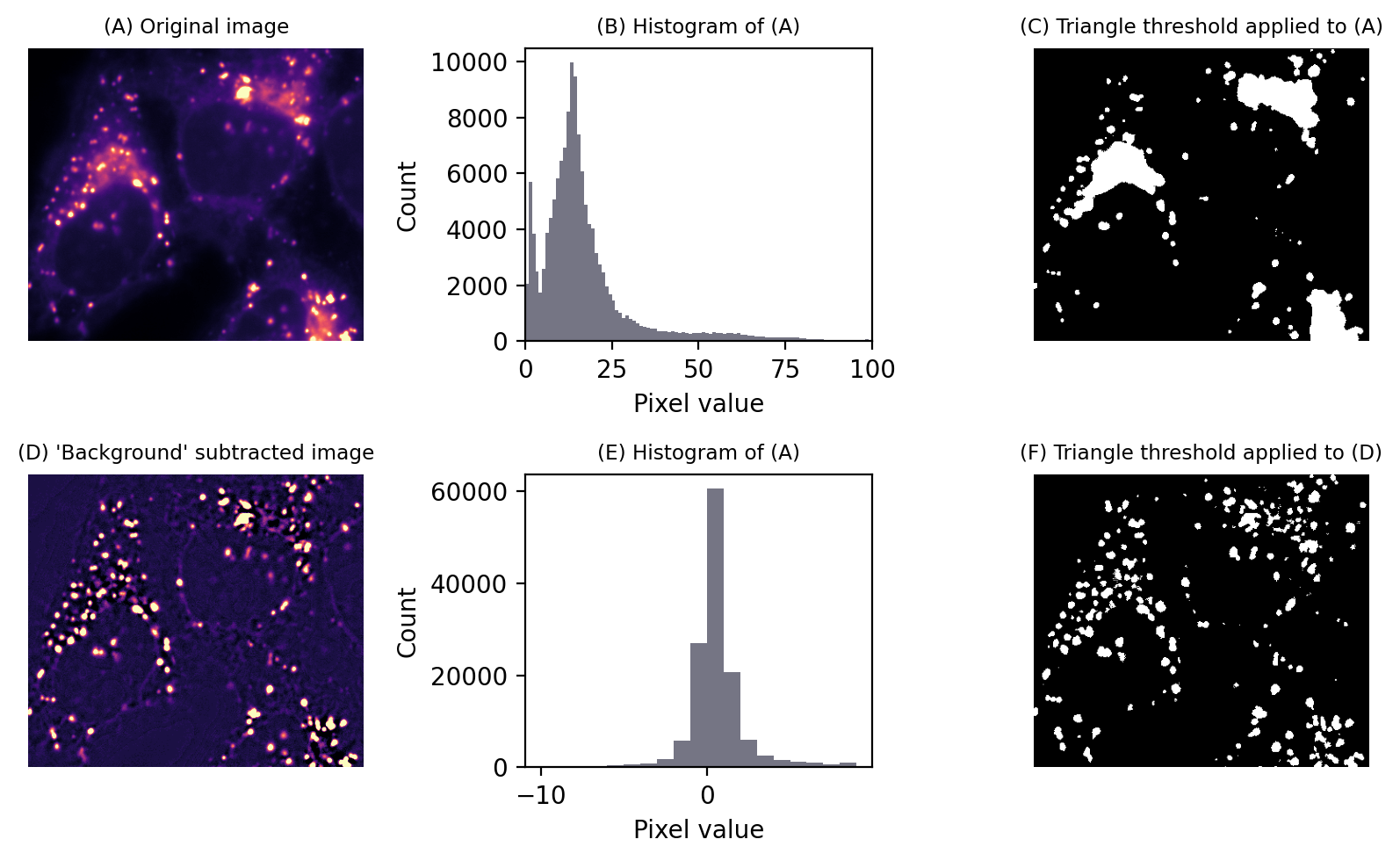
../../../_images/5fa110b73abb402cdaa9f27d08452452d9dd7e51170efeaca402e228b8c15d3b.png — Figura 77 Umbral para detectar estructuras que aparecen sobre un fondo variable. Ningún umbral global puede ser suficientemente selectivo *(fila superior)*. Sin embargo, si se puede crear una “imagen de fondo” (aquí usando un filtro mediano grande) y luego restarla, un único umbral puede dar resultados mucho mejores *(fila inferior)*. Esto equivale a aplicar un umbral variable a la imagen original.#

La parte difícil es crear la segunda imagen. Los filtros son la clave y el tema del próximo capítulo [next chapter] (chap_filters).