Tamaño y dimensiones de píxeles#
Outline del capítulo
El concepto de tamaño de píxel relaciona las medidas en píxeles con unidades físicas
Puede resultar útil pensar en los píxeles como pequeños cuadrados, pero esto es una simplificación.
El número de dimensiones de una imagen es el número de datos necesarios para identificar cada píxel.
Show code cell content
%load_ext autoreload
%autoreload 2
# Default import
import sys
sys.path.append('../../../')
from helpers import *
import numpy as np
from matplotlib import pyplot as plt
Introducción#
Esperemos que a estas alturas estés apropiadamente nervioso por cambiar accidentalmente los valores de los píxeles y, por lo tanto, comprometer la integridad de tu imagen. En caso de duda, siempre calcularás histogramas u otras medidas antes y después de probar algo nuevo, para comprobar si los píxeles han cambiado.
Este capítulo explora los píxeles a más detalle, incluyendo cómo se organizan dentro de una imagen y cómo se relacionan con las cosas del mundo físico.
Tamaño de píxel#
¿Qué tamaño tiene un píxel?
En cierto sentido, un píxel es sólo un número: en realidad no tiene tamaño alguno. Sin embargo, si no nos ponemos demasiado filosóficos al respecto[^philosophy], sabemos intuitivamente que las cosas representadas en nuestras imágenes generalmente tienen un tamaño en la vida real.
El “tamaño de píxel” es una idea que nos ayuda a traducir las medidas que hacemos en imágenes a los tamaños y posiciones de las cosas en la vida real. A menudo necesitamos saber el tamaño de píxel de nuestras imágenes para que los resultados de nuestro análisis sean significativos.
Una forma de pensar en esto en microscopía es considerar el campo de visión de una imagen, es decir, el ancho y el alto del área de la que se ha tomado la imagen. Podemos dividir el ancho y el alto en unidades físicas (a menudo µm) por el número de píxeles a lo largo de esa dimensión, como se muestra en Figura 35.
El resultado es que tenemos dos valores en µm/px, correspondientes al ancho de píxel y alto de píxel. Por lo general estos son iguales.
Show code cell source
# Crop center of an image to a target shape (sz,sz)
im_orig = load_image('sunny_cell.tif')
sz = 600
r = (im_orig.shape[0]-sz) // 2
c = (im_orig.shape[1]-sz) // 2
im_orig = im_orig[r:r+sz, c:c+sz, ...]
from skimage.transform import downscale_local_mean, resize
from scipy.ndimage import zoom
im_orig = resize(im_orig, (512, 512))
fig = create_figure()
n_plots = 6
for ii in range(n_plots):
# Downscale if we need to
if ii > 0:
im = downscale_local_mean(im_orig, (2**ii, 2**ii))
else:
im = im_orig.copy()
# Compute image and pixel sizes
len_pixels = im.shape[0]
len_microns = 64
pixel_size = len_microns/len_pixels
# Show the image
# We need to 'zoom' it to be the same size as the original so that the
# arrows line up exactly across figures
s = im_orig.shape[0]
show_image(zoom(im, 2**ii, order=0), pos=(2, 3, ii+1))
color_pixels = (0.6, 0.2, 0.2, 0.9)
color_microns = (0.2, 0.2, 0.6, 0.9)
arrow_args = dict(
xycoords='data',
arrowprops=dict(arrowstyle="<->", shrinkA=0, shrinkB=0, color=color_pixels),
annotation_clip=False,
text=""
)
text_args = dict(
fontsize='x-small'
)
offset = s/15
plt.annotate(xy=(0,-offset), xytext=(s,-offset), **arrow_args)
plt.text(s/2, -offset*1.5, f'{len_pixels} px', ha='center', **text_args, color=color_pixels)
plt.annotate(xy=(s+offset,0), xytext=(s+offset,s), **arrow_args, color=color_pixels)
plt.text(s+offset*1.5, s/2, f'{len_pixels} px', **text_args, va='center', ha='left', rotation='vertical', color=color_pixels)
arrow_args['arrowprops']['color'] = color_microns
plt.annotate(xy=(0,s+offset), xytext=(s,s+offset), **arrow_args)
plt.text(s/2, s+offset*1.5, f'{len_microns} µm', va='top', ha='center', **text_args, color=color_microns)
plt.annotate(xy=(-offset,0), xytext=(-offset,s), **arrow_args)
plt.text(-offset*1.5, s/2, f'{len_microns} µm', **text_args, va='center', ha='right', rotation='vertical', color=color_microns)
plt.title(f'Pixel size {pixel_size} µm/px', pad=20, fontsize='small')
plt.tight_layout(pad=1.5)
plt.show()
glue_fig('fig_pixel_size', fig)

Figura 35 Imágenes con diferentes tamaños de píxeles. Siempre que el campo visual sigue siendo el mismo, el tamaño de píxel aumenta a medida que disminuye el número de píxeles de la imagen.#

Figura 36 Un píxel no es un pequeño cuadrado#
Cuadratura de píxeles
Hablar de píxeles como si tuvieran (generalmente) valores iguales de ancho y alto hace que parezcan muy cuadrados, pero anteriormente dije que los píxeles no son cuadrados: simplemente se muestran usando cuadrados.
Esta distinción filosófica ligeramente turbia se considera en el memorando técnico de Alvy Ray Smith (derecha), cuyo título da una buena impresión del argumento central. En resumen, llevar demasiado lejos el modelo de que los píxeles son cuadrados conduce a confusión al final (por ejemplo, ¿qué pasaría en sus “bordes”?), y realmente no coincide con la realidad de cómo se registran las imágenes (es decir, valores de píxeles). no se determinan detectando la luz emitida desde pequeñas regiones cuadradas, consulte Desenfoque y Función de dispersión de punto (Point Spread Function o PSF por sus siglas en inglés)). A menudo se utilizan términos alternativos, como distancia de muestreo, en lugar de tamaño de píxel, y son potencialmente menos engañosos.
Pero el “tamaño de píxel” todavía se usa comúnmente en software (incluyendo ImageJ), y usaremos el término como una abreviatura útil.
Tamaños y medidas de píxeles#
Conocer el tamaño de píxel permite calibrar las medidas de tamaño. Por ejemplo, si medimos alguna estructura horizontalmente en la imagen y encontramos que tiene 10 píxeles de largo, con un tamaño de píxel de 0,5 µm, podemos deducir que su longitud real en realidad es (¡aproximadamente!) 10 × 0.5 µm = 5 µm .
Esta conversión a menudo se realiza dentro del software de análisis, pero depende de que la información del tamaño de píxel esté presente y sea correcta. Si todo va bien, se habrán escrito los tamaños de píxeles apropiados en un archivo de imagen durante la adquisición y posteriormente el software los habrá leído. Desafortunadamente, esto no siempre funciona (consulte Archivos y formatos de archivo) y, por lo tanto, siempre debemos verificar que nuestros tamaños de píxeles y las medidas de tamaño derivadas sean razonables.
Supongamos que detectamos una estructura y contamos que cubre un área que abarca 10 píxeles. Supongamos también que el ancho del píxel = 2.0 µm y la altura del píxel es 2.0 µm.
¿Cuál es el área de la estructura en µm2?
40 µm2
Al menos esa es la respuesta que estaba buscando: 10 x 2 µm x 2 µm = 40 µm2.
Si quieres ser pedante al respecto, podrías tener objeciones sobre si tiene sentido reportar áreas 2D para estructuras 3D o el posible impacto del error de medición causado por el límite de difracción.
Pero no seamos pedantes por ahora.
Tamaños de píxeles y detalles#
En general, si el tamaño de píxel en una imagen de microscopía es grande, entonces no podemos ver detalles muy finos (consulte Figura 35). Sin embargo, el tema se complica por la difracción de la luz cuando consideramos escalas de cientos de nanómetros, de modo que adquirir imágenes con tamaños de píxeles más pequeños no necesariamente nos aporta información adicional, e incluso podría convertirse en un obstáculo.
Esto se explorará a más detalle en Desenfoque y Función de dispersión de punto (Point Spread Function o PSF por sus siglas en inglés) y Ruido.
Dimensiones#
Identificando dimensiones#
El concepto de dimensiones de imagen es en su mayoría sencillo, aunque no conozco ninguna definición universal que todas las personas y todo el software sigan de manera confiable.
El enfoque que adoptaremos aquí es decir: el número de dimensiones es el número de datos que necesitas saber para identificar un píxel individual.
Por ejemplo, en las imágenes 2D más familiares, podemos identificar de forma única un píxel si conocemos sus coordenadas espaciales x e y.
Pero si necesitáramos saber las coordenadas x e y, un número de sección z, un canal de color y un punto de tiempo, entonces estaríamos trabajando con datos 5D (fig-dimensions ). Podríamos descartar una de estas dimensiones (cualquiera) y obtener una imagen 4D, y continuar hasta que nos quede un solo píxel: una imagen 0D.
Si desechamos ese píxel, ya no tendremos imagen.
Show code cell content
fig = create_figure(figsize=(8, 6))
im_full = load_image('mitosis-single.zip', volume=True)
im_full = np.moveaxis(im_full, 1, -1)
im_full = im_full.astype(np.float32)
im_full = im_full - np.percentile(im_full, 0.1)
im_full /= np.percentile(im_full, 99.9)
im_full = np.clip(im_full * 255, 0, 255).astype(np.uint8)
im_3d = np.squeeze(im_full[im_full.shape[0]//2, ...])
im_3d = np.flipud(im_3d)
im_2d = np.squeeze(im_3d[..., 1])
im_1d = np.squeeze(im_2d[im_2d.shape[0]//2, ...])
im_0d = np.squeeze(im_1d[im_1d.shape[0]//2, ...])
from matplotlib import gridspec
gs = gridspec.GridSpec(2, 6)
ax = plt.subplot(gs[0, 1:3])
show_image('images/dims_0.png', title='(A) 0 dimensional', axes=ax)
ax = plt.subplot(gs[0, 3:5])
show_plot(im_1d, title='(B) 1 dimensional (x)', axes=ax)
ax = plt.subplot(gs[1, 0:2])
show_image(im_2d, vmin=0, vmax=255, title='(C) 2 dimensional (xy)', axes=ax)
ax = plt.subplot(gs[1, 2:4])
show_image(create_rgb(im_3d, colors=['magenta', 'green'], axis=-1), title='(D) 3 dimensional (xyc)', axes=ax)
ax = plt.subplot(gs[1, 4:6])
show_image('images/mitosis4d.png', title='(E) 4 dimensional (xycz)', axes=ax)
plt.tight_layout()
glue_fig('fig_dimensions', fig)
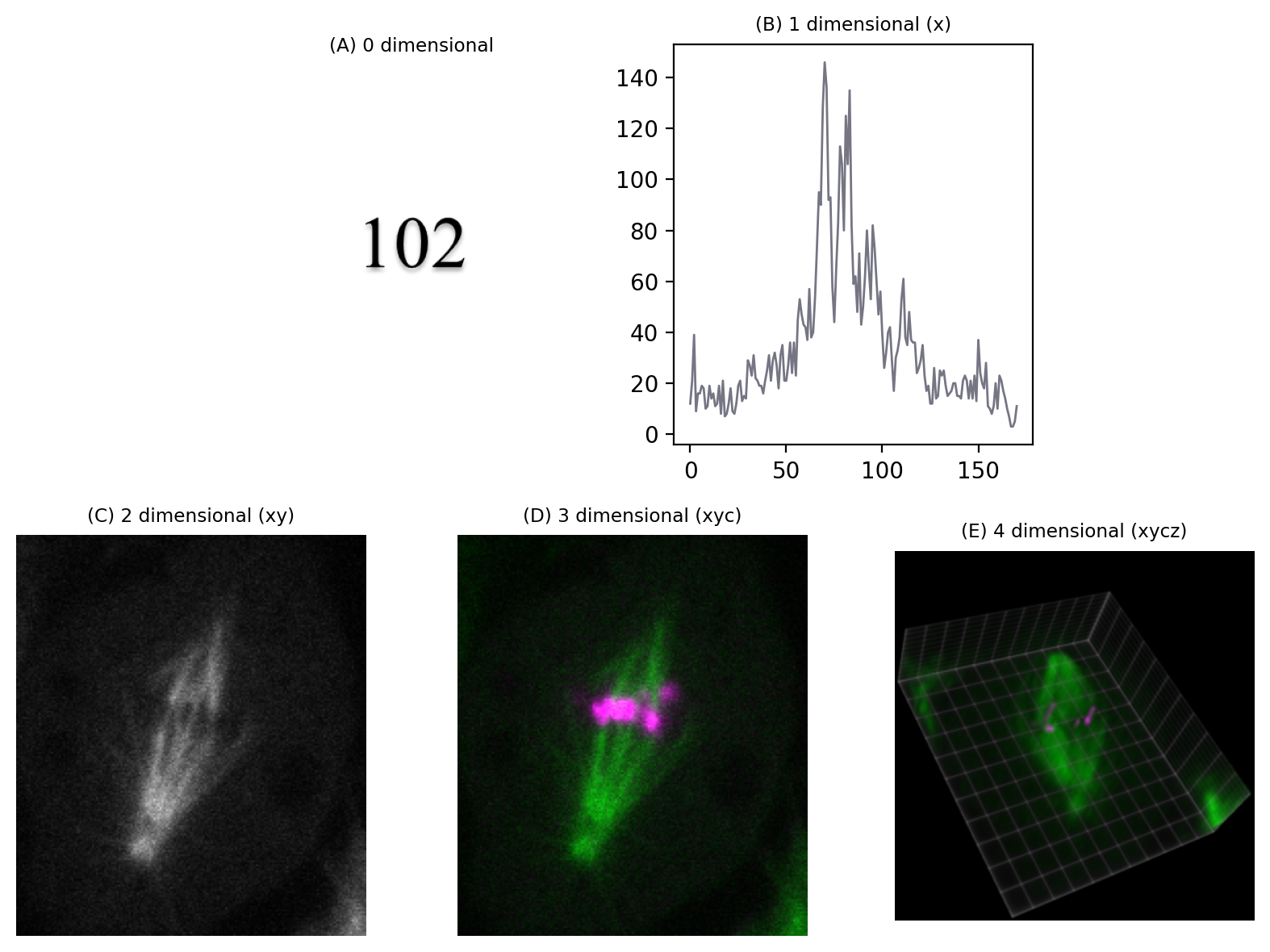
Figura 37 Representaciones de imágenes con diferente número de dimensiones. (A) Se considera que un valor único tiene 0 dimensiones. (B–E) Se agregan dimensiones adicionales, aquí en el siguiente orden: coordenada x (1), coordenada y (2), número de canal (3), sección z (4). La vista de volumen en (E) se generó utilizando el [ClearVolume plugin for Fiji] (https://imagej.net/plugins/clearvolume).#
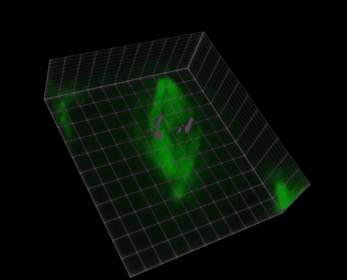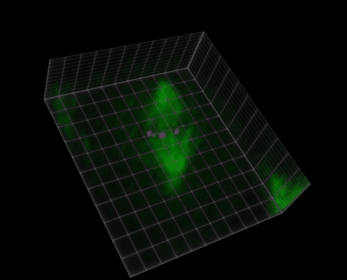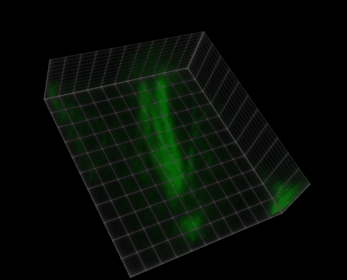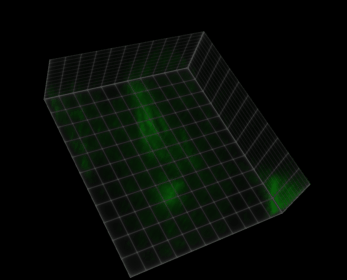
Figura 38 Visualización de una imagen 5D (xyczt) usando ClearVolume + Fiji.#
Por lo tanto, en principio, las imágenes 2D no necesitan tener dimensiones x e y. Las dimensiones podrían ser x y z, o y y tiempo, por ejemplo. Pero si bien podemos jugar con la identidad de las dimensiones, algo es cierto: una imagen nD requiere n piezas de información para identificar cada píxel.
¿Los canales realmente añaden una dimensión?
Puede haber cierta confusión en la idea de dimensiones, particularmente cuando se trata de canales. Si seguimos rigurosamente el enfoque anterior, una imagen con x, y y canales sería 3D… pero en la práctica dichas imágenes a menudo (¡pero no siempre!) se llaman 2D de todos modos.
“3D” a veces se limita a significar que hay una dimensión z. Si tenemos una imagen con x, y y time entonces técnicamente sería correcto llamarla 3D, pero es probable que resulte confuso, por lo que probablemente sea mejor referirse a ella como “serie de tiempo”.
Sigo pensando que nuestra explicación del número de dimensiones como «el número de cosas que necesitas saber para identificar un píxel» es una buena forma básica de conceptualizarlo y corresponde bien con la implementación en software y el uso en Python/ NumPy. Pero debemos estar preparados para utilizar el contexto para identificar cuándo la palabra «dimensiones» se utiliza con imágenes de manera más informal.
Proyecciones Z#
Cuantas más dimensiones tengamos, más complicado puede resultar visualizar la imagen completa de forma eficaz.
Las pilas Z se componen de diferentes imágenes 2D (llamadas secciones o slices) adquiridas a diferentes profundidades focales, opcionalmente con una dimensión de canal adicional agregada.
Una forma de visualizar una pila z es simplemente mirar cada segmento individualmente.
Show code cell content
im = load_image('confocal-series.zip', volume=True)
# Drop last slice (for space reasons)
im = im[:-1, ...]
# Make the channels the last dimension
if im.shape[1] == 2:
im = np.moveaxis(im, 1, -1)
# Drop some spatial info too
im = im[:, ::2, ::2, :]
# Convert to float32 and rescale per channel (to simplify display later)
def rescale_per_channel(im: np.ndarray, min_percentile=0.25, max_percentile=99.75):
im = im.astype(np.float32)
for c in range(im.shape[-1]):
im[..., c] = im[..., c] - np.percentile(im[..., ], 0.25)
im[..., c] = im[..., c] / np.percentile(im[..., ], 99.75)
return im
im = rescale_per_channel(im)
# Not used, but uncomment to visualize what happens to noisier images
# rng = np.random.default_rng(100)
# im = im + rng.normal(scale=0.1, size=im.shape)
# Not used... but uncomment to test code works for 8-bit as well
# im = np.clip(im * 255, 0, 255).astype(np.uint8)
# Dimension order now ZHWC
n_slices = im.shape[0]
fig = create_figure(figsize=(12, 8))
for ii in range(n_slices):
show_image(create_rgb(im[ii,...], ('green', 'magenta')),
pos=(4, n_slices//4, ii+1), vmin=0, vmax=1, title=f'Slice {ii+1}')
# plt.tight_layout()
glue_fig('fig_dimensions_slices', fig)
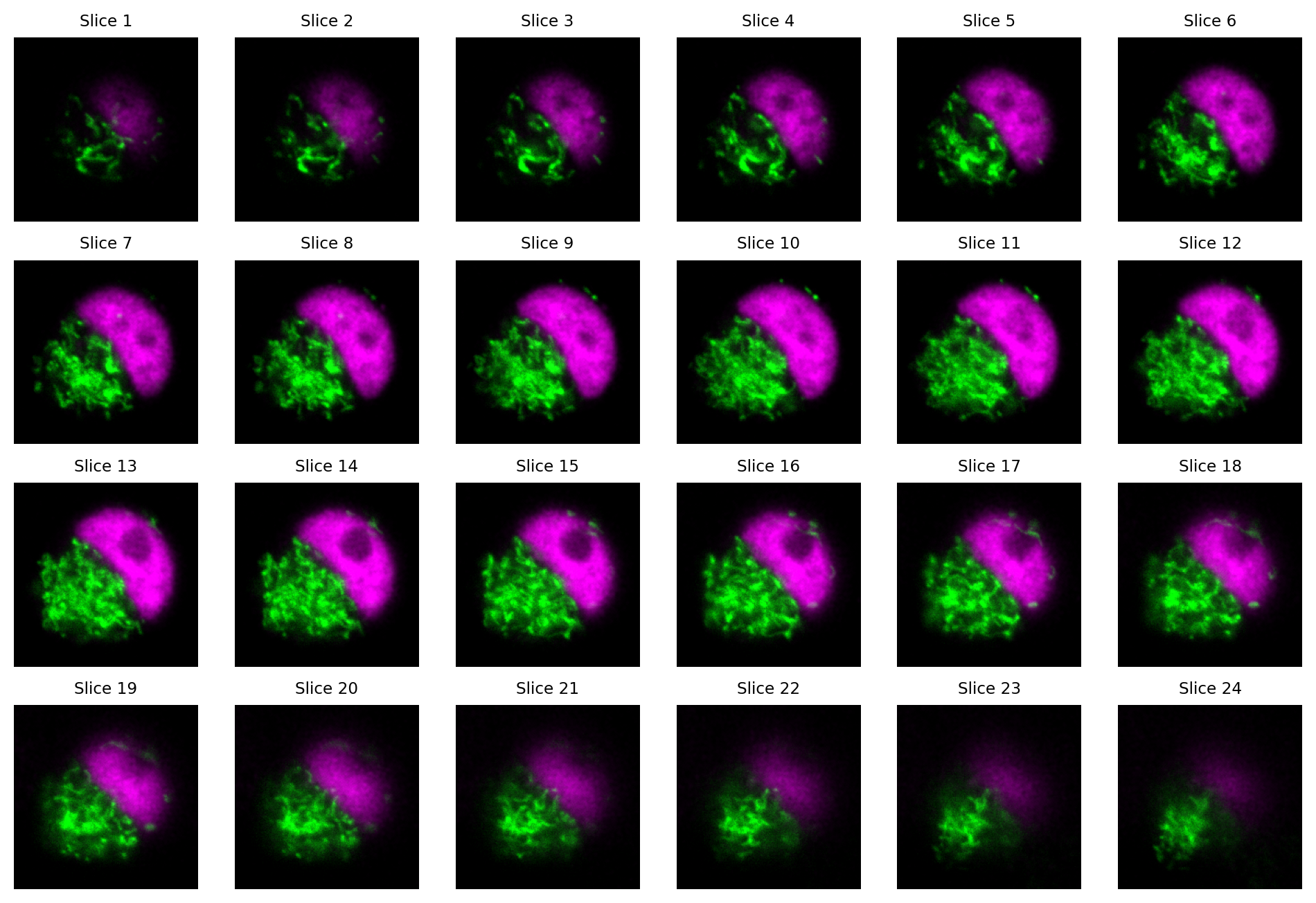
Figura 39 Visualizar los cortes de una pila z como imágenes separadas. Aquí, cada segmento tiene 2 canales.#
¿Cuántas dimensiones tiene la pila z en Figura 39?
Recuerda: ¡aquí contamos los canales como una dimensión!
La imagen es 4D: canales x, y, z.
Ver muchas porciones por separado es engorroso.
Una forma eficaz de resumir la información en una pila z es calcular una proyección z.
Esto genera una nueva imagen con la dimensión z esencialmente eliminada, es decir, una imagen 3D se vuelve 2D o una imagen 4D se vuelve 3D.
Los valores de píxeles en la imagen de output dependen de qué función se utilizó para calcular la proyección. Quizás lo más común sea utilizar una proyección z máxima. Para cada ubicación de píxel en la nueva imagen, el valor máximo se toma en todos los cortes z en la ubicación de píxel correspondiente en la imagen original (es decir, las mismas coordenadas x, y, c y t, según corresponda).
Show code cell content
im = load_image('confocal-series.zip', volume=True)
# Drop last slice (for space reasons)
im = im[:-1, ...]
# Make the channels the last dimension
if im.shape[1] == 2:
im = np.moveaxis(im, 1, -1)
# Drop some spatial info too
im = im[:, ::2, ::2, :]
# Convert to float32 and rescale per channel (to simplify display later)
im = rescale_per_channel(im)
fig = create_figure(figsize=(12, 4))
# Compute projections; retain the same dtype in the output
projections = [
('Minimum projection', im.min(axis=0).astype(im.dtype)),
('Mean (average) projection', im.mean(axis=0).astype(im.dtype)),
('Maximum projection', im.max(axis=0).astype(im.dtype)),
('Standard deviation projection', im.std(axis=0).astype(im.dtype)),
# # We could justify rescaling the standard deviation for display, because it could be very different from the others
# ('Standard deviation projection', rescale_per_channel(im.std(axis=0).astype(im.dtype))),
]
n_proj = len(projections)
for ii, (name, im_proj) in enumerate(projections):
show_image(create_rgb(im_proj, ('green', 'magenta')), pos=(1, n_proj, ii+1),
title=name, vmin=0, vmax=1)
glue_fig('fig_dimensions_projection', fig)
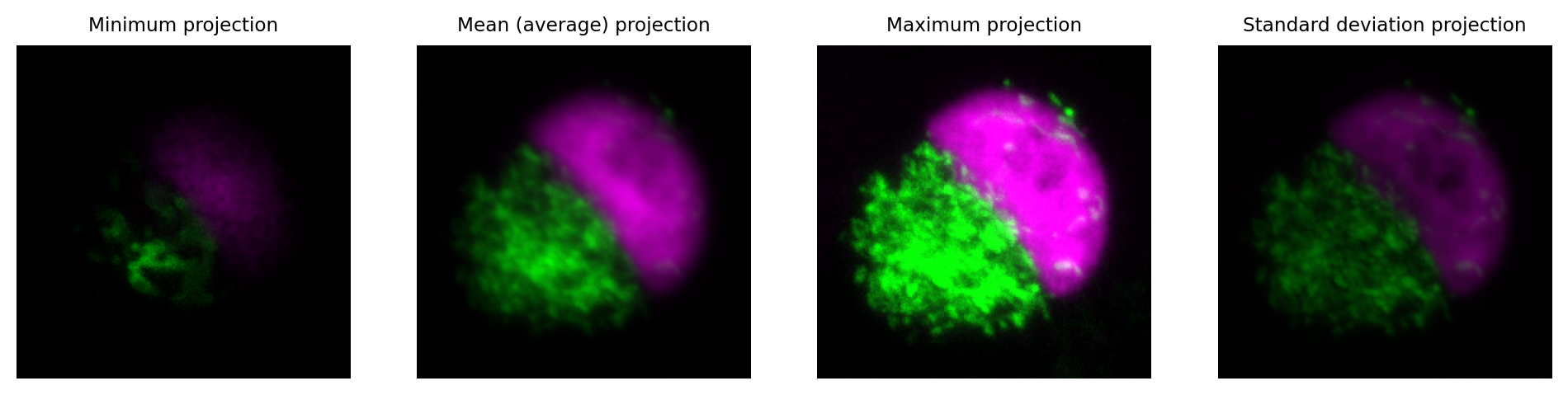
Figura 40 Visualizando una pila z usando proyecciones z.#
Secciones ortogonales#
Otra forma útil de visualizar información de la pila z es utilizar cortes ortogonales.
Conceptualmente, el la pila z se ve como un bloque de píxeles 3D (o quizás, 4D si contamos los canales). Elegimos un único punto en la imagen y generamos tres vistas ortogonales de la imagen que pasan por ese punto. Podemos pensar que estamos mirando el bloque desde tres ángulos diferentes: desde arriba y desde dos lados adyacentes.
Esto nos da 3 imágenes, como se muestra en Figura 41. Cada imagen depende del único punto por el que pasan las vistas ortogonales.
Show code cell content
im = load_image('confocal-series.zip', volume=True)
# Make the channels the last dimension
if im.shape[1] == 2:
im = np.moveaxis(im, 1, -1)
# Drop some spatial info since the detail doesn't help make the figure any clearer
im = im[:, ::2, ::2, :]
# Convert to float32 and rescale per channel (to simplify display later)
im = im.astype(np.float32)
for c in range(im.shape[-1]):
im[..., c] = im[..., c] - np.percentile(im[..., ], 0.25)
im[..., c] = im[..., c] / np.percentile(im[..., ], 99.75)
def show_orthogonal(im, axes, loc=None, projection=None, colors=('green', 'magenta'), show_slices=False, title=None):
"""
Show orthogonal slices or projections.
"""
from mpl_toolkits.axes_grid1 import make_axes_locatable
if axes is None:
fig = create_figure()
ax = fig.gca()
else:
ax = axes
if loc is None and projection is None:
loc = tuple(s//2 for s in im.shape)
# Create axes for orthogonal views
divider = make_axes_locatable(ax)
ax_xz = divider.append_axes("bottom", 0.5, pad=0.1, sharex=ax)
ax_yz = divider.append_axes("left", 0.5, pad=0.1, sharey=ax)
# Generate slices or projections
if projection:
imxy = projection(im, axis=0)
imxz = projection(im, axis=2)
imyz = np.moveaxis(projection(im, axis=1), 0, 1)
else:
imxy = im[loc[0],...]
imxz = im[:, loc[1],...]
imyz = np.moveaxis(im[:, :, loc[2],:], 0, 1)
show_image(create_rgb(imyz, colors),
axes=ax_yz, vmin=0, vmax=1)
if show_slices:
ax_yz.plot([loc[0], loc[0]], [0, im.shape[2]-1], 'w--', linewidth=1)
ax_yz.set_xlabel('z')
ax_yz.set_xticks([])
ax_yz.set_ylabel('y', rotation=0, va='center', ha='right')
ax_yz.set_yticks([])
ax_yz.set_axis_on()
show_image(create_rgb(imxy, colors),
axes=ax,
vmin=0, vmax=1)
if show_slices:
row = loc[1]
col = loc[2]
ax.plot([0, im.shape[1]-1], [row, row], 'w--', linewidth=1)
ax.plot([col, col], [0, im.shape[2]-1], 'w--', linewidth=1)
show_image(create_rgb(imxz, colors),
axes=ax_xz,
vmin=0, vmax=1)
if show_slices:
ax_xz.plot([0, im.shape[1]-1], [loc[0], loc[0]], 'w--', linewidth=1)
ax_xz.set_xlabel('x')
ax_xz.set_xticks([])
ax_xz.set_ylabel('z', rotation=0, va='center', ha='right')
ax_xz.set_yticks([])
ax_xz.set_axis_on()
plt.tight_layout()
if title:
ax.set_title(title)
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
show_orthogonal(im, show_slices=True, axes=axes[0], loc=(2, 50, 50))
show_orthogonal(im, show_slices=True, axes=axes[1])
show_orthogonal(im, show_slices=True, axes=axes[2], loc=(20, 150, 120))
glue_fig('fig_dimensions_orthogonal', fig)
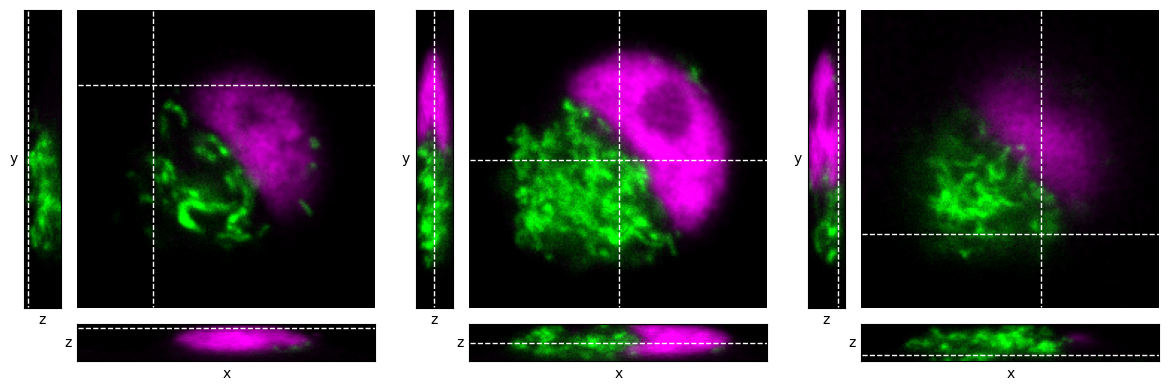
Figura 41 Visualización de una pila z utilizando cortes ortogonales en diferentes ubicaciones dentro de una pila z, indicadas por líneas discontinuas.#
La idea de vistas y proyecciones ortogonales se puede combinar para generar proyecciones ortogonales, como se muestra en Figura 42. En este caso, no necesitamos elegir un punto por el cual pasar, porque las proyecciones no dependen de una ubicación de corte específica; más bien, todos los píxeles contribuyen a cada proyección.
Show code cell content
im = load_image('confocal-series.zip', volume=True)
# Make the channels the last dimension
if im.shape[1] == 2:
im = np.moveaxis(im, 1, -1)
# Drop some spatial info since the detail doesn't help make the figure any clearer
im = im[:, ::2, ::2, :]
# Convert to float32 and rescale per channel (to simplify display later)
im = im.astype(np.float32)
for c in range(im.shape[-1]):
im[..., c] = im[..., c] - np.percentile(im[..., ], 0.25)
im[..., c] = im[..., c] / np.percentile(im[..., ], 99.75)
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
show_orthogonal(im, projection=np.min, title='Orthogonal min projection', axes=axes[0])
show_orthogonal(im, projection=np.mean, title='Orthogonal mean projection', axes=axes[1])
show_orthogonal(im, projection=np.max, title='Orthogonal max projection', axes=axes[2])
glue_fig('fig_dimensions_orthogonal_projections', fig)
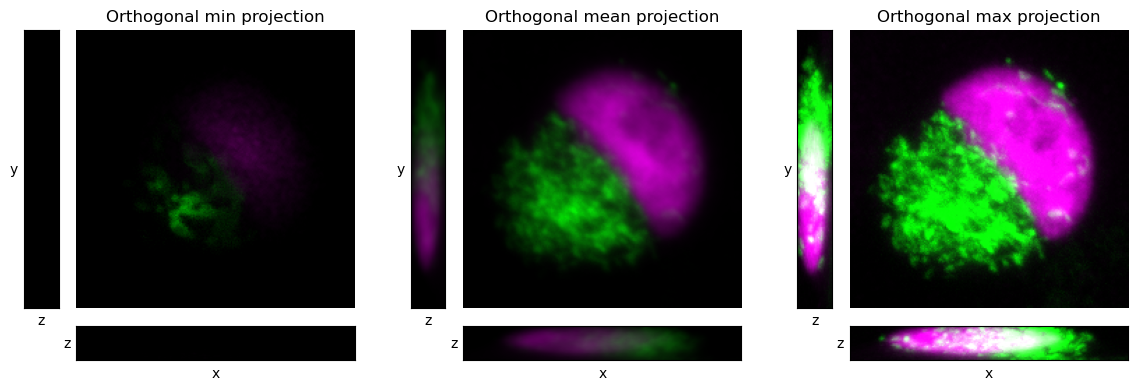
Figura 42 Visualizando una pila z usando proyecciones ortogonales.#

