Operaciones morfológicas#
Outline del capítulo
Las operaciones morfológicas se pueden utilizar para refinar o modificar las formas de los objetos en las imágenes.
Se pueden aplicar muchas operaciones morfológicas a imágenes binarias para mejorar la segmentación de una imagen.
Las operaciones morfológicas en escala de grises también se pueden utilizar como pasos de procesamiento antes de la binarización o para ayudar a identificar máximos y mínimos regionales.
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Los filtros y umbrales de imagen nos permiten detectar estructuras de diversas formas y tamaños para diferentes aplicaciones. Sin embargo, a pesar de nuestros mejores esfuerzos, las imágenes binarias producidas por nuestros umbrales a menudo todavía contienen regiones detectadas inexactas o indeseables. Podrían beneficiarse de una limpieza adicional.
En esta etapa, estamos trabajando principalmente con formas (morfología), por lo que la mayoría de las técnicas que describimos aquí a menudo se denominan operaciones morfológicas.
Operaciones morfológicas utilizando filtros de clasificación.#
Show code cell content
"""
Show morphological operations.
Note that, as a habit, I use 'bw_' at the beginning of variable names for
variables that are really binary (black/white) images to identify these
from other images, for which I use 'im_'.
"""
def create_disk(radius: int):
"""
Create a circular structuring element.
This is essentially the binary/morphological equivalent the filter kernel.
"""
r = radius
x = np.arange(-r, r+1)
y = np.arange(-r, r+1)
y, x = np.meshgrid(x, x)
return x*x + y*y <= r*r
# Create structuring element
radius = 2
strel = create_disk(radius)
# Erode, dilate, open & close the corresponding images
# Use > 0 when reading to ensure they are binary ('bool') arrays,
# not 8-bit images that happen to just have two values in them.
bw_erode = load_image('images/morph_erode.png') > 0
bw_eroded = ndimage.binary_erosion(bw_erode, structure=strel)
bw_dilate = load_image('images/morph_dilate.png') > 0
bw_dilated = ndimage.binary_dilation(bw_dilate, structure=strel)
bw_open = load_image('images/morph_open.png') > 0
bw_opened = ndimage.binary_opening(bw_open, structure=strel)
bw_close = load_image('images/morph_close.png') > 0
bw_closed = ndimage.binary_closing(bw_close, structure=strel)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 4))
show_image(np.vstack((bw_erode, bw_eroded)), title="(A) Erosion", pos=141)
show_image(np.vstack((bw_dilate, bw_dilated)), title="(B) Dilation", pos=142)
show_image(np.vstack((bw_open, bw_opened)), title="(C) Opening", pos=143)
show_image(np.vstack((bw_close, bw_closed)), title="(D) Closing", pos=144)
glue_fig('fig_erode_dilate_open', fig)
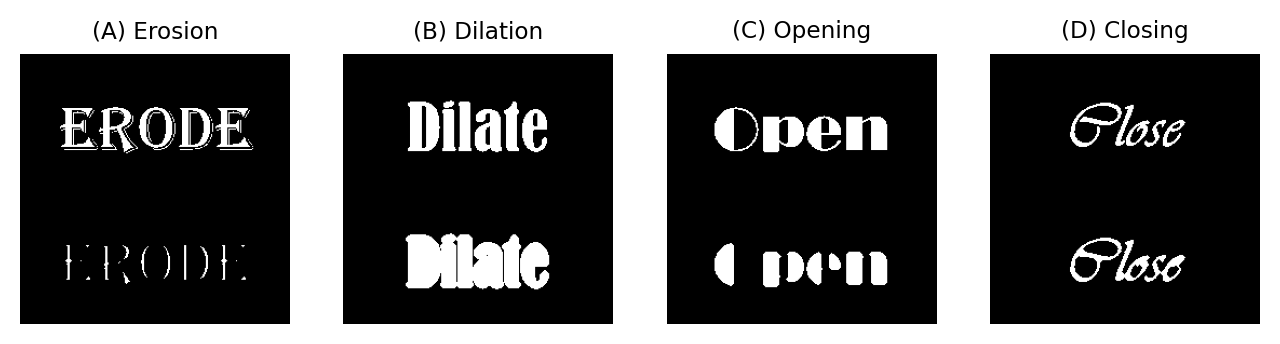
Figura 102 Descripción general de la erosión, dilatación, apertura y cierre. La imagen original se muestra en la parte superior, mientras que la parte procesada se muestra en la parte inferior en cada caso.#
Erosión y dilatación#
Nuestras dos primeras operaciones morfológicas, erosión y dilatación, son en realidad idénticas al filtrado mínimo y máximo respectivamente, descrito en el capítulo anterior. Los nombres erosión y dilatación se utilizan con más frecuencia cuando se habla de imágenes binarias, pero las operaciones son las mismas independientemente del tipo de imagen.
Elementos estructurantes
La vecindad utilizada para calcular el resultado de cada píxel se define mediante un elemento estructurante. Esto es similar a un núcleo de filtro, excepto que solo tiene valores 0 y 1 (para ignorar o incluir el píxel vecino, respectivamente).
La erosión hará que los objetos en la imagen binaria sean más pequeños, porque un píxel se establecerá en el valor de fondo si cualquier otro píxel en el vecindario está en el fondo. Esto puede dividir objetos individuales en varias partes.
Por el contrario, la dilatación hace que los objetos sean más grandes, ya que la presencia de un solo píxel en primer plano en cualquier lugar del vecindario dará como resultado un output del primer plano. Esto también puede hacer que los objetos se fusionen.
Show code cell content
def load_spots() -> np.ndarray:
im = load_image('hela-cells.zip')[50:400, 50:450, 0].astype(np.float32)
return im
def load_binary_spots(method='median') -> np.ndarray:
"""
Create a small, imperfect binary image containing spots.
We don't try to optimize preprocessing or thresholds - we just want something for illustration.
"""
import skimage.filters as filters
import skimage.morphology as morph
im = load_spots()
if method == 'median':
im_bg = ndimage.median_filter(im, (15, 15))
im = im - im_bg
elif method == 'opening':
im_bg = morph.opening(im, morph.disk(10))
im = im - im_bg
elif method == 'dog':
sigma = 2.5
im = filters.gaussian(im, sigma) - filters.gaussian(im, sigma*1.6)
bw = im > filters.threshold_triangle(im)
return bw
# Define radius (change this to update the figure!)
radius = 2
# Create structuring element
strel = create_disk(radius)
# Load image & process
bw = load_binary_spots()
bw_eroded = ndimage.binary_erosion(bw, structure=strel)
bw_dilated = ndimage.binary_dilation(bw, structure=strel)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw_eroded, title=f"(B) Erosion (radius={radius})", pos=132)
show_image(bw_dilated, title=f"(C) Dilation (radius={radius})", pos=133)
plt.tight_layout()
glue_fig('fig_erode_dilate_spots', fig)
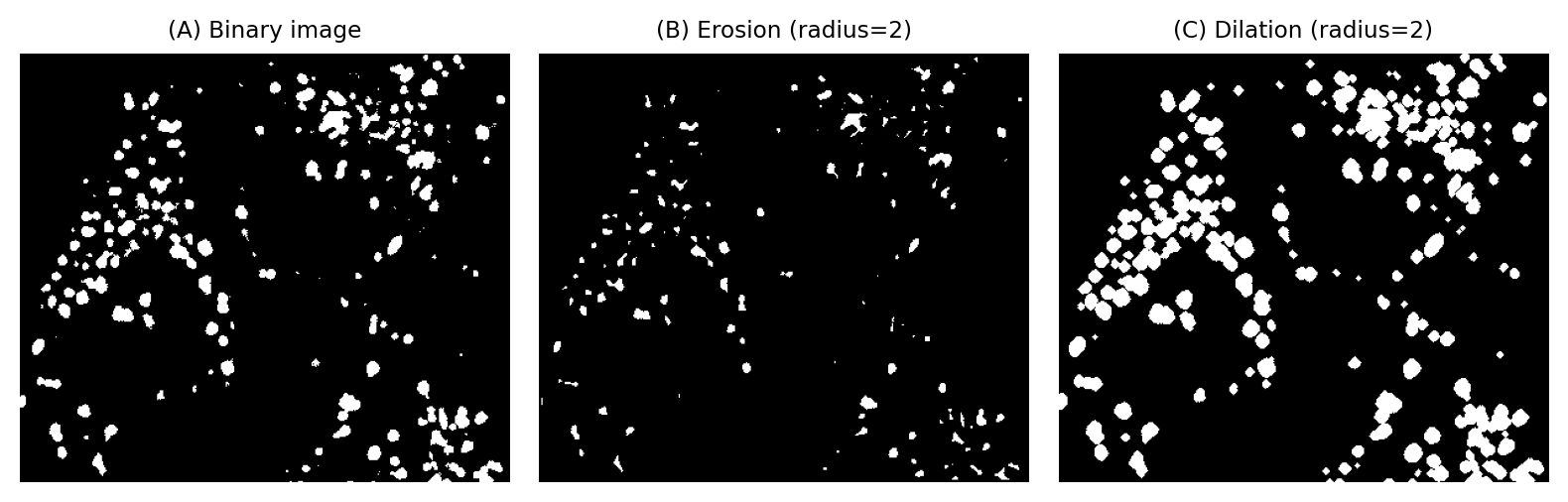
Figura 103 Los efectos de la erosión y la dilatación en una imagen binaria de estructuras pequeñas.#
Apertura y cierre#
El hecho de que la erosión y la dilatación por sí solas afecten los tamaños puede ser un problema: puede que nos gusten sus capacidades para fusionar, separar o eliminar objetos, pero preferimos que tengan menos impacto sobre áreas y volúmenes. Combinar ambas operaciones ayuda a lograrlo.
Apertura consiste en una erosión seguida de una dilatación. Por lo tanto, primero reduce los objetos y luego expande lo que queda hasta aproximadamente su tamaño original.
Un proceso así no es tan inútil como podría parecer a primera vista. Si la erosión hace que objetos muy pequeños desaparezcan por completo, es evidente que la dilatación no puede hacerlos reaparecer: han desaparecido para siempre. Los objetos apenas conectados y separados por la erosión tampoco se vuelven a conectar mediante el paso de dilatación.
Cerrar es lo opuesto a abrir, es decir, una dilatación seguida de una erosión, y de manera similar cambia las formas de los objetos. La dilatación puede provocar que objetos casi conectados se fusionen y, a menudo, estos permanecen fusionados después del paso de erosión. Si deseas contar objetos, pero están mal subdivididos en la segmentación, cerrar puede ayudar a que los recuentos sean más precisos.
Show code cell content
# Define radius (change this to update the figure!)
radius = 2
# Create structuring element
strel = create_disk(radius)
# Load image & process
bw = load_binary_spots()
bw_opened = ndimage.binary_opening(bw, structure=strel)
bw_closed = ndimage.binary_closing(bw, structure=strel)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw_opened, title=f"(B) Opened (radius={radius})", pos=132)
show_image(bw_closed, title=f"(C) Closed (radius={radius})", pos=133)
plt.tight_layout()
glue_fig('fig_open_close_spots', fig)

Figura 104 Los efectos de apertura y cierre en una imagen binaria de pequeñas estructuras. A diferencia de cuando se utiliza únicamente la erosión o la dilatación, los tamaños de los objetos se conservan en gran medida aunque se modifican los contornos. La apertura tiene el efecto de eliminar completamente los objetos más pequeños o delgados.#
Límites y contornos#
Podemos hacer uso de las operaciones anteriores para identificar contornos en una imagen binaria. Para hacer esto, primero necesitamos una definición clara de lo que entendemos por «contorno».
El límite interior se puede definir como los píxeles de primer plano que son adyacentes a los píxeles de fondo. Podemos determinar el límite interior mediante
Duplicar la imagen binaria
Erosión con elemento estructurante 3×3
Restando la imagen erosionada del original
El límite exterior puede definirse como los píxeles de fondo que son adyacentes a los píxeles de primer plano. Podemos determinar el límite exterior mediante
Duplicar la imagen binaria
Dilatando con un elemento estructurante 3×3
Restando la imagen original de la imagen dilatada
Límites más gruesos
No hay razón para limitar los contornos a un grosor de 1 píxel. La elección de un elemento estructurante de mayor tamaño permite crear contornos más gruesos. También podríamos restar una imagen erosionada de una imagen dilatada para identificar un límite más grueso que contenga píxeles tanto internos como externos.
Una aplicación de la creación de límites gruesos en imágenes microscópicas de células es generar una imagen binaria de los núcleos y luego una segunda imagen binaria que represente un anillo alrededor del núcleo. Esto hace posible realizar mediciones que probablemente se realicen dentro del citoplasma, justo fuera del núcleo, sin la tarea de identificar el área completa de la célula, lo que a menudo resulta difícil si la célula o la membrana no son claramente visibles.
Show code cell content
# Define radius (change this to update the figure!)
radius = 3
# Create structuring element
strel = create_disk(radius)
# Load image & process
bw = load_binary_spots()
bw_eroded = ndimage.binary_erosion(bw, structure=strel)
bw_dilated = ndimage.binary_dilation(bw, structure=strel)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw ^ bw_eroded, title=f"(B) Inner boundaries (radius={radius})", pos=132)
show_image(bw_dilated ^ bw, title=f"(C) Outer boundaries (radius={radius})", pos=133)
plt.tight_layout()
glue_fig('fig_binary_outlines', fig)

Figura 105 Calcular límites interiores y exteriores, mediante erosión o dilatación. El radio del elemento estructurante se puede utilizar para ajustar el espesor del límite.#
Encontrar mínimos y máximos locales#
La erosión y la dilatación se pueden utilizar para encontrar píxeles que son máximos locales o mínimos locales muy fácilmente, con la salvedad de que los resultados son inexactos y, a menudo, inutilizables. Sin embargo, el truco funciona «lo suficientemente bien» con suficiente frecuencia como para que valga la pena conocerlo.
Aquí nos centramos en los máximos. El proceso para detectar mínimos locales es idéntico, excepto que la imagen debe invertirse o usarse erosión en lugar de dilatación.
Un máximo local se puede definir como un píxel con un valor mayor que todos sus vecinos, o un grupo conectado de píxeles con el mismo valor mayor que los píxeles circundantes. Una manera fácil de detectar estos píxeles es dilatar la imagen con un filtro máximo de 3×3 y verificar los valores de píxeles que no han cambiado (es decir, donde el píxel ya era un máximo dentro de su vecindad).
Esto es inexacto porque no sólo identifica los máximos; también detecta algunas «mesetas» donde los píxeles tienen valores idénticos a los de sus vecinos. En la práctica, esto no siempre es un problema porque el ruido puede hacer que las mesetas sean prácticamente inexistentes en muchas imágenes del mundo real (al menos en aquellas que no han sido recortadas).
Un problema mayor es que el enfoque a menudo identifica demasiados máximos para ser útil (Figura 106).
Show code cell content
from skimage import morphology as morph
from skimage import filters as filters
from skimage.segmentation import mark_boundaries
# Load image & process
im = load_spots()
im_dilated = ndimage.maximum_filter(im, (3, 3))
bw = im == im_dilated
im2 = im - np.percentile(im.ravel(), 0.5)
im2 = im2 / np.percentile(im2.ravel(), 99.5)
im_boundaries = mark_boundaries(np.clip(im2, 0, 1), bw, color=(1, 0, 0))
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(im, clip_percentile=0.5, title="(A) Grayscale image", pos=221)
show_image(im_dilated, title=f"(B) 3×3 dilation of (A)", pos=222)
show_image(bw, title=f"(C) Pseudo-maxima where (A) == (B)", pos=223)
show_image(im_boundaries, title=f"(C) Overlay of pseudo maxima", pos=224)
plt.tight_layout()
glue_fig('fig_morph_simple_maxima', fig)
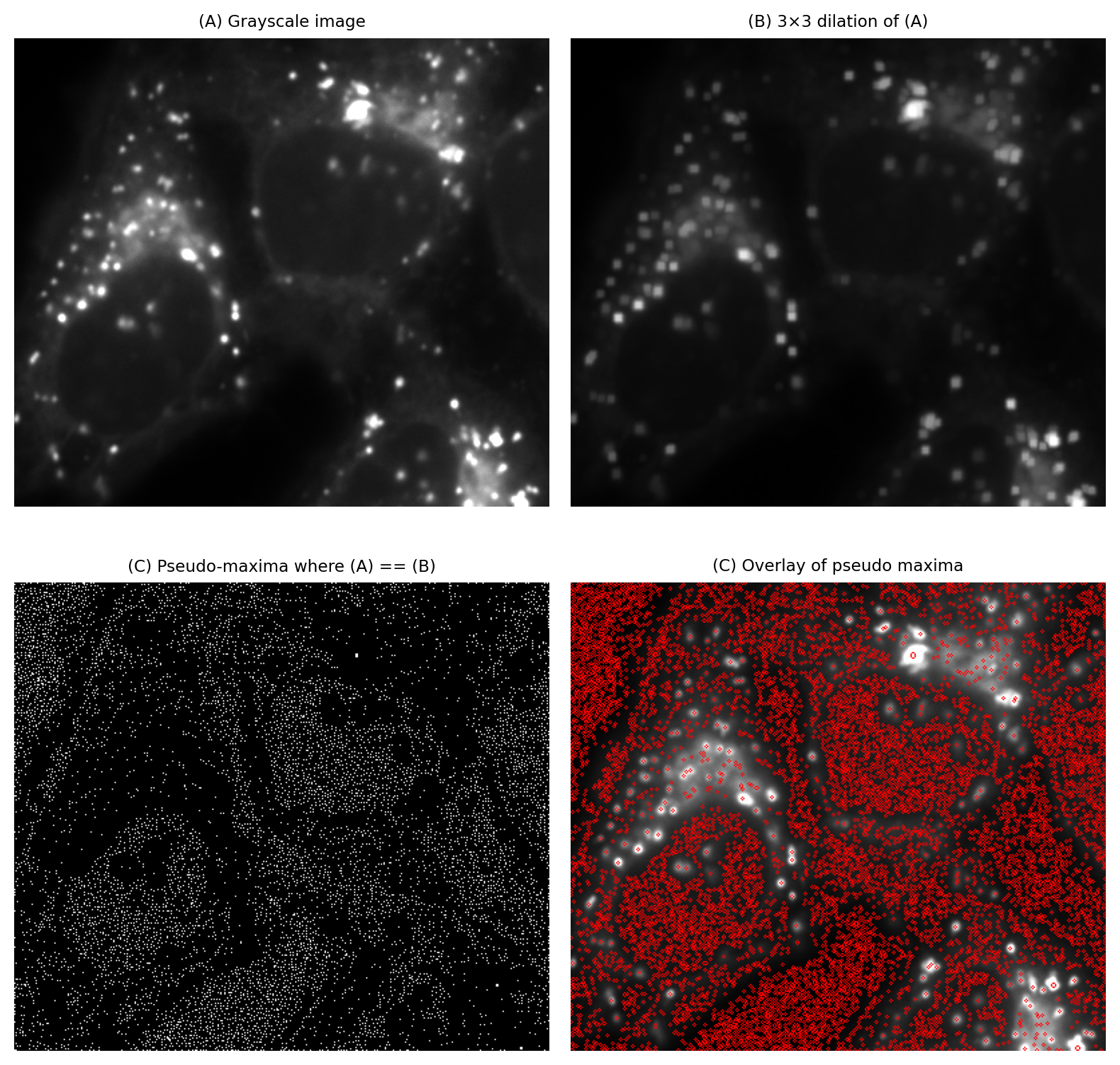
Figura 106 La identificación de máximos locales con la ayuda de una dilatación de 3 × 3 tiende a encontrar demasiados máximos para ser útil.#
Podemos reducirlos aumentando el tamaño del filtro máximo (por lo tanto, requiriendo que los píxeles sean máximos en una región más grande) o suavizando previamente la imagen (generalmente con un [filtro Gaussiano] (sec_filters_gaussian)). Sin embargo, ajustar los parámetros resulta difícil.
Veremos un enfoque alternativo que suele ser más intuitivo en H-Máxima y H-Mínima.
Show code cell content
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
# Load image & process
im = load_spots()
im_dilated = ndimage.maximum_filter(im, (7, 7))
bw = im == im_dilated
im2 = im - np.percentile(im.ravel(), 0.5)
im2 = im2 / np.percentile(im2.ravel(), 99.5)
im_boundaries = mark_boundaries(np.clip(im2, 0, 1), bw, color=(1, 0, 0))
show_image(im, clip_percentile=0.5, title="(A) Grayscale image", pos=221)
show_image(im_dilated, title=f"(B) 7×7 dilation of (A)", pos=222)
show_image(bw, title=f"(C) Pseudo-maxima where (A) == (B)", pos=223)
show_image(im_boundaries, title=f"(C) Overlay of pseudo maxima", pos=224)
plt.tight_layout()
glue_fig('fig_morph_simple_maxima_bigger', fig)

Figura 107 Identificar máximos locales con la ayuda de una dilatación mayor (aquí, 7 × 7 píxeles) a veces puede dar mejores resultados que usar una dilatación más pequeña Figura 106.#
Más operaciones morfológicas#
Apertura de área#
Apertura de área es similar a apertura, excepto que evita la necesidad de cualquier tipo de filtrado máximo o mínimo.
Funciona identificando componentes conectados en la imagen binaria, que son regiones contiguas de píxeles de primer plano. Para cada componente conectado, se cuenta el número de píxeles para obtener un área en px². Si el área de un componente cae por debajo de un umbral de área específico, los píxeles de ese componente se colocan en el fondo, es decir, el componente se elimina.
La apertura del área es a menudo preferible a la apertura, porque no tiene ningún impacto en la forma de cualquier estructura mayor que el umbral del área. Simplemente aplica un umbral de área mínimo, eliminando todo lo más pequeño.
Show code cell content
# Define areas (change this to update the figure!)
small_area = 10
large_area = 100
from skimage import morphology as morph
# Load image & process
bw = load_binary_spots()
bw_small_opened = morph.area_opening(bw, small_area)
bw_large_opened = morph.area_opening(bw, large_area)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw_small_opened, title=f"(B) Small area opening ({small_area} px²)", pos=132)
show_image(bw_large_opened, title=f"(C) Large area opening ({large_area} px²)", pos=133)
plt.tight_layout()
glue_fig('fig_area_open_spots', fig)

Figura 108 Utilizar la apertura del área para retirar objetos pequeños.#
Relleno de agujeros#
Rellenar huecos implica identificar componentes conectados de píxeles de fondo que están completamente rodeados por píxeles de primer plano. Luego, estos componentes se «invierten» para convertirse en píxeles de primer plano.
Si luego queremos identificar los agujeros, podemos restar la imagen original de la imagen rellena.
Show code cell content
from skimage import morphology as morph
# Load image & process
im = load_image('happy_cell.tif')
bw = im > im.mean()
bw_filled = ndimage.binary_fill_holes(bw)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw_filled, title=f"(B) Holes filled", pos=132)
show_image(bw_filled.astype(np.uint8) - bw.astype(np.uint8), title=f"(C) Result of (B) - (A)", pos=133)
plt.tight_layout()
glue_fig('fig_fill_holes_cell', fig)
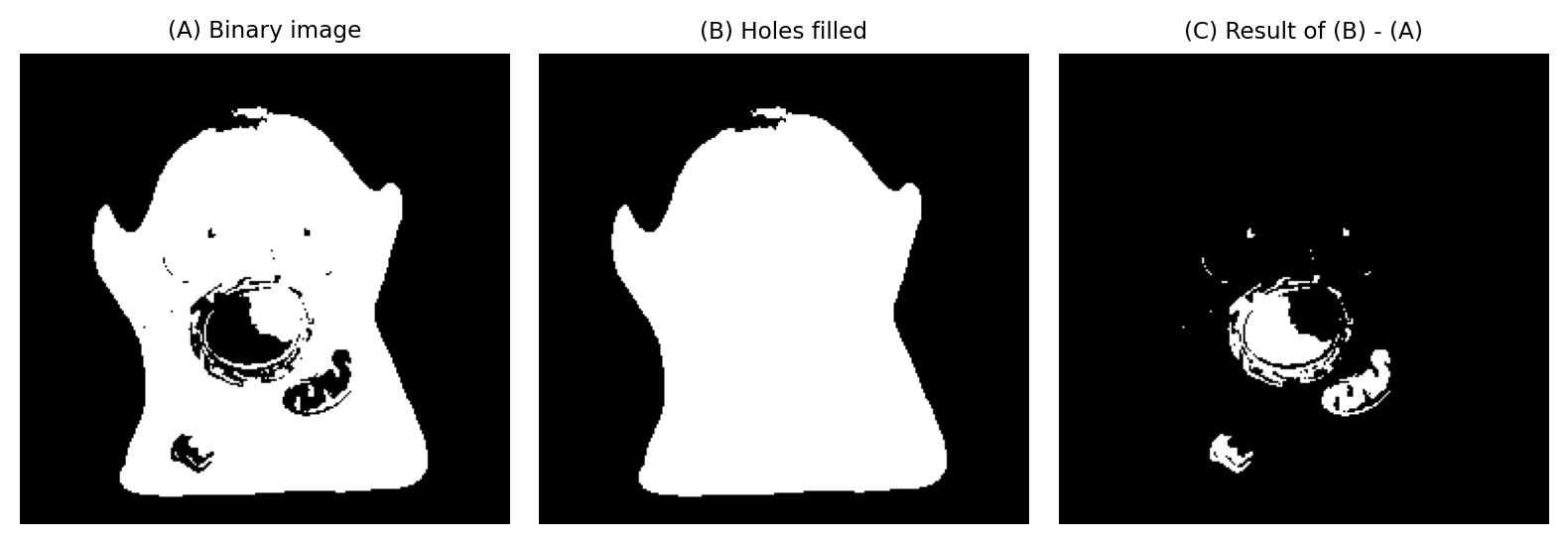
Figura 109 Rellenar agujeros en una imagen binaria. La sustracción de imágenes permite extraer los propios agujeros.#
Show code cell content
# Code to selective fill small holes
im = load_image('happy_cell.tif')
bw = im > im.mean()
bw2 = ~bw
bw2 = morph.area_opening(bw2, 1000)
bw2 = ~bw2
fig = create_figure(figsize=(2, 2))
show_image(bw2)
glue_fig('fig_fill_small_holes_cell', fig)

Figura 110 Pequeños agujeros llenos.#
No siempre queremos llenar todos los huecos dentro de una imagen binaria, sino sólo los más pequeños. ¿Se te ocurre una forma de rellenar sólo agujeros de menos de 1000 px², utilizando la apertura de área?
Necesitarás al menos una operación descrita en el capítulo anterior.
Una forma de rellenar agujeros por debajo de un tamaño fijo:
Invertir la imagen binaria
Realizar apertura de área con un umbral de área de 1000 px²
invertir el resultado
Adelgazamiento y esqueletización#
Adelgazamiento y esqueletizacion son operaciones relacionadas que tienen como objetivo «adelgazar» objetos en una imagen binaria solo hasta sus líneas centrales. Son particularmente útiles con estructuras filamentosas o tubulares, como axones o vasos sanguíneos.
Show code cell content
im = load_image('happy_cell.tif')
bw = im > im.mean()
bw = ndimage.binary_fill_holes(bw)
bw_thinned = morph.thin(bw)
bw_skeletonized = morph.skeletonize(bw)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 4))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw_thinned, title="(B) Thinned image", pos=132)
show_image(bw_skeletonized, title="(C) Skeletonized image", pos=133)
plt.tight_layout()
glue_fig('fig_binary_thinning', fig)
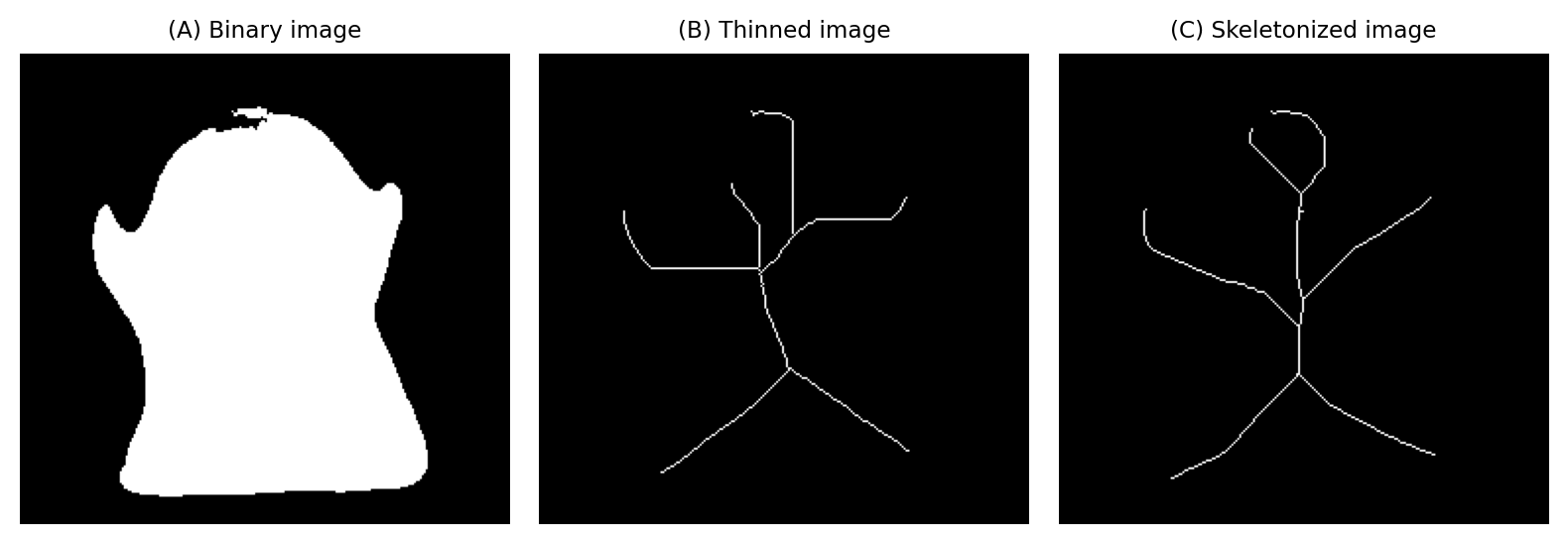
Figura 111 Los efectos del adelgazamiento y la esqueletización en una imagen binaria.#
¿Cuál es la diferencia entre adelgazamiento y esqueletización?
La verdad es que no estoy del todo seguro. Hay bastante superposición en la literatura y he visto el mismo algoritmo al que se hace referencia con ambos nombres. Además, existen diferentes algoritmos de adelgazamiento que dan diferentes resultados; la situación es similar para los algoritmos de esqueletización.
En ocasiones, el software ofrece tanto adelgazamiento como esqueletización, pero a menudo sólo ofrece uno u otro. Vale la pena probar cualquier método de adelgazamiento/esqueletización disponible para ver cuál funciona mejor para una aplicación en particular.
Reconstrucción morfológica#
La reconstrucción morfológica es una técnica algo avanzada que sustenta varias operaciones poderosas de procesamiento de imágenes. Es útil tanto con imágenes binarias como en escala de grises.
La reconstrucción morfológica requiere dos imágenes del mismo tamaño: una imagen de marcador y una imagen de máscara. Todos los píxeles de la imagen de máscara deben tener valores mayores o iguales a los píxeles correspondientes de la imagen de marcador.
El algoritmo de reconstrucción dilata progresivamente la imagen del marcador (por ejemplo, aplica un filtro máximo de 3 × 3), mientras restringe el marcador para que permanezca «dentro» de la máscara; es decir, nunca se permite que los valores de píxeles del marcador excedan los valores de la máscara. Esta dilatación se repite iterativamente hasta que el marcador no puede cambiar más sin exceder la máscara. El resultado es la nueva imagen del marcador, después de que se hayan realizado todas las dilataciones.
Algunos ejemplos ayudarán a demostrar cómo funciona esto y por qué es útil. La diferencia crucial en los métodos siguientes es cómo se crean las imágenes de marcador y máscara.
Umbral de histéresis#
Un uso de la reconstrucción morfológica es implementar un umbral doble, también conocido como umbral de histéresis.
Esto implica definir un umbral bajo y un umbral alto. El umbral bajo funciona como cualquier umbral global para identificar regiones. Sin embargo, una región se descarta de la imagen binaria si no contiene también al menos un píxel que supere el umbral alto.
Esto se logra mediante la reconstrucción morfológica definiendo el marcador como todos los píxeles que exceden el umbral alto y la máscara como todos los píxeles que exceden el umbral bajo. Los marcadores se expandirán para llenar las regiones de máscara que los contienen. Pero cualquier región de máscara que no contenga píxeles marcadores simplemente se ignora.
Show code cell content
from skimage import morphology as morph
# Load image & process
im = load_spots()
bw_low = im > im.mean() + im.std()
bw_high = im > im.mean() + 3 * im.std()
bw_hist = morph.reconstruction(bw_high, bw_low)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(im, clip_percentile=0.5, title="(A) Grayscale image", pos=221)
show_image(bw_low, title="(B) Mask image (low threshold)", pos=222)
show_image(bw_high, title=f"(C) Marker image (high threshold)", pos=223)
show_image(bw_hist, title=f"(D) Reconstruction result (hysteresis threshold)", pos=224)
plt.tight_layout()
glue_fig('fig_hysteresis_threshold_spots', fig)

Figura 112 Aplicar un umbral de histéresis a una imagen. El tamaño y el área de los objetos detectados por este método están determinados por el umbral bajo, pero al menos uno de los valores de píxel dentro del objeto debe exceder el umbral alto. Esto mitiga ligeramente el problema de que un único umbral global tenga [un gran impacto en los resultados del análisis] (chap_thresholding), ya que el mismo umbral influye simultáneamente tanto en lo que se detecta como en su tamaño.#
H-Máxima y H-Mínima#
Vimos anteriormente que podríamos (más o menos) identificar máximos locales de una manera muy simple usando una dilatación de imagen, pero los resultados a menudo son demasiado inexactos para ser útiles.
H-Maxima y H-Minima pueden ayudarnos a superar esto. Ambas operaciones requieren solo un parámetro intuitivo: nos permiten identificar máximos o mínimos utilizando un umbral de intensidad local H.
Esto se logra mediante la reconstrucción morfológica. Para H-maxima, el proceso es:
Establece la imagen original en escala de grises como máscara
Resta H de la máscara para crear los marcadores
Aplicar reconstrucción morfológica utilizando los marcadores y la máscara.
Resta el resultado de la reconstrucción de la máscara
Obten el umbral de la imagen sustraída con un umbral global de H
Los pasos principales se ilustran en Figura 113. Podemos aplicar el mismo proceso a una imagen invertida para encontrar H-mínimo.
Show code cell content
from skimage import morphology as morph
from skimage import filters as filters
from skimage.segmentation import mark_boundaries
# Load image & process
im = load_spots()
h = im.std()
im_recon = morph.reconstruction(im - h, im)
bw = morph.h_maxima(im, h)
im2 = im - np.percentile(im.ravel(), 0.5)
im2 = im2 / np.percentile(im2.ravel(), 99.5)
im_boundaries = mark_boundaries(np.clip(im2, 0, 1), bw, color=(1, 0, 0))
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(im, clip_percentile=0.5, title="(A) Grayscale image", pos=221)
show_image(im_recon, clip_percentile=0.5, title=f"(B) Morphological reconstruction result", pos=222)
show_image(im - im_recon, clip_percentile=0.5, title=f"(C) Result of (A) - (B)", pos=223)
show_image(im_boundaries, title=f"(C) H-maxima as an overlay", pos=224)
plt.tight_layout()
glue_fig('fig_morph_h_maxima', fig)

Figura 113 Cálculo de H-máximos mediante reconstrucción morfológica. Aquí, H se establece (arbitrariamente) como la desviación estándar de la imagen.#
Apertura y cierre por reconstrucción.#
H-maxima y H-minima utilizan la reconstrucción morfológica para generar eficazmente una imagen de fondo que se puede restar del original. Hacemos esto restando una constante H, que actúa como un umbral de intensidad local.
También podemos usar la reconstrucción morfológica para generar una imagen de fondo basada en información espacial, en lugar de un umbral de intensidad H, usando apertura por reconstrucción. Esto efectivamente introduce un componente de tamaño en nuestro umbral local. El cierre por reconstrucción es una operación análoga que se puede definir mediante el cierre morfológico.
El punto de partida para la apertura por reconstrucción es una apertura morfológica [como se define anteriormente] (sec_morph_opening_closing), es decir, una erosión seguida de una dilatación. Esto define la imagen del marcador. La imagen original se utiliza como máscara.
Show code cell content
from skimage import morphology as morph
radius = 10
# Load image & process
im = load_spots()
im_open = morph.opening(im, morph.disk(radius))
im_recon = morph.reconstruction(im_open, im)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(im, clip_percentile=0.5, title="(A) Grayscale image", pos=221)
show_image(im_open, clip_percentile=0.5, title=f"(B) Morphological opening (radius={radius})", pos=222)
show_image(im_recon, clip_percentile=0.5, title=f"(C) Opening by reconstruction (radius={radius})", pos=223)
show_image(im - im_recon, clip_percentile=0.5, title=f"(D) Result of (A) - (C)", pos=224)
plt.tight_layout()
glue_fig('fig_morph_reconstruct_opening', fig)

Figura 114 Utilizar apertura por reconstrucción para obtener una estimación de fondo. La estimación se puede restar de una imagen antes de aplicar un umbral global.#
Como antes, la apertura por sí sola elimina estructuras que son más pequeñas que el elemento estructurante, mientras afecta ligeramente las formas de todo lo demás. La apertura por reconstrucción esencialmente agrega algunas dilataciones adicionales (restringidas) para que las estructuras que no fueron eliminadas sean más similares a como eran originalmente. Esto puede hacer que la apertura por reconstrucción sea más atractiva para generar imágenes de fondo que se utilizarán para la resta.
La apertura por reconstrucción también se puede aplicar a imágenes binarias como una alternativa a la apertura y la apertura de área. Al igual que la apertura de área, la apertura por reconstrucción puede eliminar algunos objetos manteniendo exactamente las formas de objetos más grandes.
Show code cell content
from skimage import morphology as morph
radius = 3
# Load image & process
bw = load_binary_spots()
bw_open = morph.opening(bw, morph.disk(radius))
bw_opening_by_recon = morph.reconstruction(bw_open, bw)
# Show original concatenated with the filtered images
fig = create_figure(figsize=(8, 8))
show_image(bw, title="(A) Binary image", pos=131)
show_image(bw_open, title=f"(B) Morphological opening (radius={radius})", pos=132)
show_image(bw_opening_by_recon, title=f"(C) Opening by reconstruction (radius={radius})", pos=133)
plt.tight_layout()
glue_fig('fig_morph_reconstruct_opening_binary', fig)

Figura 115 Utilizar la apertura por reconstrucción para eliminar objetos pequeños (y delgados) de una imagen binaria, conservando al mismo tiempo la forma original de todo lo que queda.#

