Transformaciones de imagen#
Outline del capítulo
La transformada de watershed se puede utilizar para dividir estructuras usando valores de intensidad
La transformada de distancia calcula la distancia entre los píxeles de primer plano y de fondo en una imagen binaria.
Las transformadas de distancia y watershed se pueden combinar para separar estructuras redondas
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Una transformada de imagen convierte una imagen en alguna otra forma, en la que los valores de píxeles pueden tener una interpretación (a veces muy) diferente.
Hay muchas formas de transformar una imagen. Nos centraremos en dos que son especialmente útiles para la segmentación y el análisis de bioimágenes: la transformada de distancia y la transformada de watershed. Presentaremos ambas brevemente, antes de mostrar cómo se pueden usar en combinación.
La transformada de distancia#
La transformada de distancia (a veces llamada transformada de distancia Euclidiana) reemplaza cada píxel de una imagen binaria con la distancia al píxel de fondo más cercano. Si el píxel en sí ya forma parte del fondo, entonces esto es cero. El resultado es una imagen llamada mapa de distancia.
Show code cell content
from scipy.ndimage import distance_transform_edt
from skimage import morphology as morph
# Create a small image
bw = np.zeros((9, 9))
bw[4, 4] = 1
bw = morph.dilation(bw, morph.disk(3))
# Compute the distance transform
im_dist = distance_transform_edt(bw)
fig = create_figure(figsize=(5, 2.5))
show_image(bw, title='Binary image', pos=121)
show_image(im_dist, title='Distance transform', pos=122)
for (i, j), z in np.ndenumerate(im_dist):
c = 'w' if z < 1 else 'k'
plt.text(j, i, str(round(z, 2)), color=c, ha='center', va='center', fontdict={'size': 5})
plt.tight_layout()
glue_fig('fig_morph_distance_detail', fig)
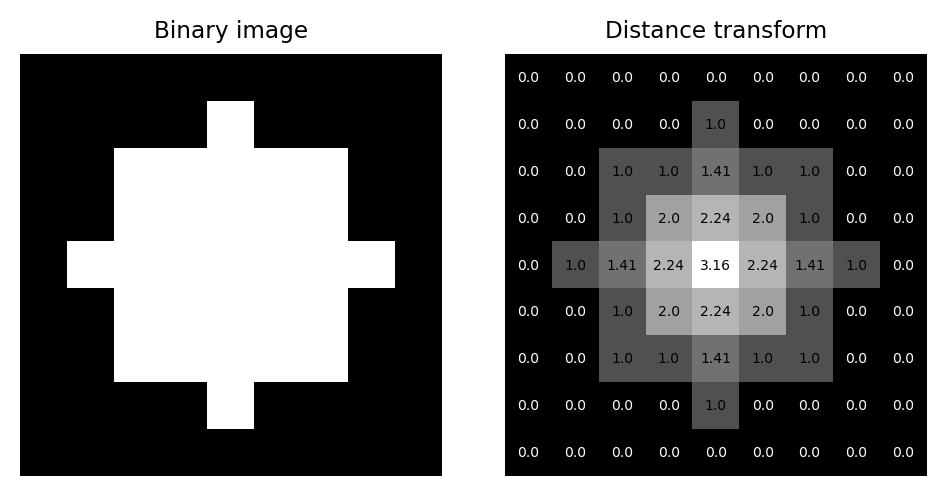
Figura 117 Una imagen binaria y su correspondiente mapa de distancia, incluyendo los valores de píxeles como superposición.#
Una pregunta natural al considerar la transformada de distancia es: ¿por qué?
Aunque su importancia puede no ser obvia inicialmente, veremos que los usos creativos de la transformada de distancia pueden ayudar a resolver algunos otros problemas de manera bastante elegante.
Por ejemplo, erosionar o dilatar imágenes binarias en gran medida puede ser muy lento, porque tenemos que usar filtros máximos o mínimos grandes. Sin embargo, la erosión y la dilatación se pueden calcular a partir de un mapa de distancias de manera muy eficiente simplemente aplicando un umbral global. Esto puede ser mucho más rápido en la práctica.
Show code cell content
im = load_image('blobs.gif')
bw = im < im.mean()
from scipy.ndimage import distance_transform_edt
im_dist = distance_transform_edt(bw)
fig = create_figure(figsize=(8, 6))
show_image(bw, title='(A) Binary image', pos=231)
show_image(im_dist, title='(B) Distance map of (A)', pos=232)
show_image(im_dist > 5, title='(C) Thresholded (B) > 5', pos=233)
im_dist_inv = distance_transform_edt(~bw)
show_image(~bw, title='(D) Binary image (inverted)', pos=234)
show_image(im_dist_inv, title='(E) Distance map of (D)', pos=235)
show_image(im_dist_inv < 5, title='(F) Thresholded (E) < 5', pos=236)
plt.tight_layout()
glue_fig('fig_morph_distance', fig)

Figura 118 Implementación de erosión (C) y dilatación (F) de imágenes binarias mediante umbrales de mapas de distancia.#
Pero el mapa de distancias contiene información útil que podemos utilizar de otras formas.
Por ejemplo, también podemos usar mapas de distancia para estimar el espesor local de una estructura. Una aplicación de esto sería evaluar los diámetros de los vasos sanguíneos. Si tenemos una imagen binaria que representa un vaso sanguíneo, podemos generar tanto un mapa de distancias como una imagen binaria adelgazada. Los valores del mapa de distancia correspondientes a los píxeles de primer plano en la imagen adelgazada proporcionan una estimación local del radio del vaso sanguíneo en ese píxel, porque el mapa de distancia proporciona la distancia al píxel de fondo más cercano y los píxeles adelgazados se producen en el centro del vaso sanguíneo.
Sin embargo, la transformada de distancia puede resultar aún más útil si la combinamos con otras transformaciones.
La transformada de watershed#
La transformada de watershed es un ejemplo de un método de crecimiento de región: comenzando desde algunas regiones semilla, las semillas se expanden progresivamente a regiones más grandes hasta que se hayan procesado todos los píxeles de la imagen. Esto proporciona una alternativa al umbral sencillo, que puede ser extremadamente útil cuando es necesario dividir una imagen en muchos objetos diferentes.
Para comprender cómo funciona la transformada de watershed, imagina la imagen como un paisaje irregular en el que el valor de cada píxel corresponde a una altura.
Show code cell content
def load_watershed_image():
im = load_image('hela-cells.zip')[:, :, 0].astype(np.float32)
im = ndimage.gaussian_filter(im, sigma=1.5)
im = im - ndimage.gaussian_filter(im, sigma=5)
r = 128
c = 75
s = 128
im = im[r:r+s, c:c+s]
im = im / im.max()
return im
# Visualize an image as a surface plot
fig = create_figure(figsize=(12, 8))
im = load_watershed_image()
show_image(im, clip_percentile=0.5, pos=131)
plt.title('Original image')
ax = fig.add_subplot(1, 3, 2, projection="3d")
X, Y = np.meshgrid(np.linspace(0, 1, im.shape[1]), np.linspace(0, 1, im.shape[0]))
ax.plot_surface(X, Y, im, color=(0.4, 0.8, 0.2), shade=True)
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_zticklabels([])
ax.set_title('Surface plot')
ax = fig.add_subplot(1, 3, 3, projection="3d")
ax.plot_surface(X, Y, -im, color=(0.4, 0.8, 0.2))
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_zticklabels([])
ax.set_title('Inverted surface plot')
glue_fig('fig_transform_surface', fig)
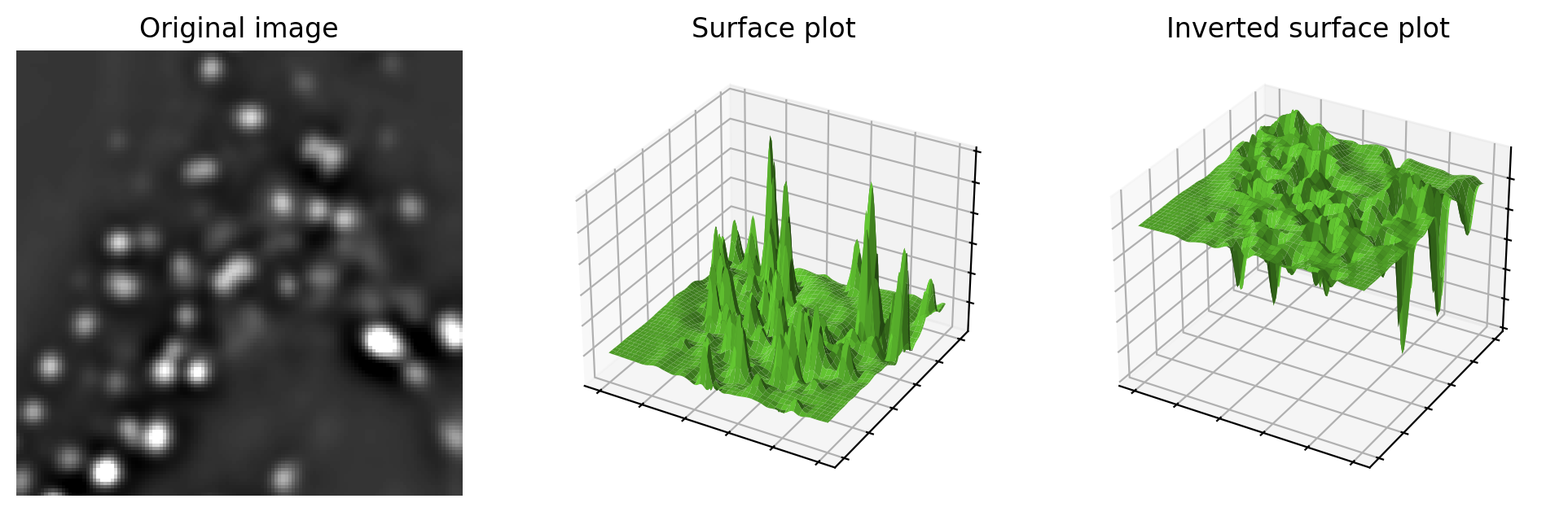
Figura 119 Visualizar una imagen como un paisaje, utilizando gráficos de superficie. Los valores de píxeles más altos generalmente se ven como picos, aunque pueden cambiarse fácilmente para convertirse en valles invirtiendo la imagen antes de producir el gráfico. Esto puede resultar útil a la hora de proporcionar información para la transformada de watershed.#
Ahora imaginemos que el agua cae uniformemente sobre esta superficie y la inunda lentamente. El agua se acumula primero en las partes más profundas; es decir, en los lugares donde los píxeles tienen valores inferiores a todos sus vecinos. Estos definen las semillas de la transformada de watershed; podemos pensar en ellos como cuencas de agua separadas.
A medida que el nivel del agua aumenta a lo largo de la imagen, ocasionalmente llegará a una cresta entre dos cuencas y, en realidad, el agua podría derramarse de una cuenca a la otra. Sin embargo, en la transformada de watershed esto no está permitido; más bien se construye una presa en esas crestas. Luego, el agua sigue subiendo y se construyen presas según sea necesario, hasta que al final cada píxel forma parte de una cuenca o de una cresta, y después hay exactamente el mismo número de cuencas que al principio.
El funcionamiento de la transformada de watershed se ilustra en el siguiente vídeo y en el resultado de ejemplo que se muestra en Figura 120.
Show code cell content
from skimage.color import label2rgb
from skimage.segmentation import watershed
from skimage.filters import threshold_triangle
from skimage.morphology.extrema import local_minima
im = load_watershed_image()
bw_mask = im > threshold_triangle(im)
# lab_seeds, n = ndimage.label(morph.h_maxima(im, im.std()/3.0))
lab_seeds, n = ndimage.label(local_minima(-im))
lab_watershed = watershed(-im, markers=None, watershed_line=True)
lab_watershed_masked = watershed(-im, markers=None, mask=bw_mask, watershed_line=True)
im2 = im - np.percentile(im, 0.25)
im2 = im2 / np.percentile(im2, 99.75)
im2 = np.clip(im2, 0, 1)
fig = create_figure(figsize=(12, 12))
show_image(label2rgb(lab_seeds, image=im2, bg_label=0, alpha=0.6), pos=221)
plt.title('Image with seeds')
show_image(label2rgb(lab_watershed, image=im2, bg_label=0), pos=222)
plt.title('Full watershed segmentation')
show_image(bw_mask, pos=223)
plt.title('Binary image (triangle threshold)')
show_image(label2rgb(lab_watershed_masked, image=im2, bg_label=0), pos=224)
plt.title('Masked watershed segmentation')
glue_fig('fig_transform_surface_watershed', fig)

Figura 120 Aplicar la transformada de watershed a una imagen. Aquí, pasamos la imagen invertida a la transformada de watershed porque queremos identificar puntos brillantes en lugar de oscuros. La transformada de watershed completa expandirá las semillas para crear una imagen etiquetada que incluya todos los píxeles, pero opcionalmente podemos enmascarar la expansión para evitar que llene el fondo. Aquí, definimos la máscara aplicando un umbral global usando el método del triángulo. Ten en cuenta que la segmentación de watershed enmascarada puede dividir algunos puntos que se fusionaron utilizando únicamente el umbral global.#
Fundamentalmente, a medida que las semillas se expanden durante la transformada de watershed, no se permite que las regiones se superpongan. Además, una vez que se ha asignado un píxel a una región, no se puede mover para formar parte de ninguna otra región.
Usando la analogía de la “lluvia cayendo sobre una superficie”, las semillas serían mínimos regionales en una imagen, es decir, píxeles con valores inferiores a todos los píxeles vecinos. Aquí es donde el agua se acumularía primero.
En la práctica, a menudo necesitamos tener más control sobre las semillas en lugar de aceptar todos los mínimos regionales (para ver por qué demasiados mínimos locales podrían ser un problema, observa que Figura 120 contiene más regiones que probablemente querríamos). Esta variación se llama transformación de watershed con semillas: la idea es la misma, pero simplemente proporcionamos las semillas explícitamente en forma de una imagen etiquetada, y las regiones crecen a partir de ellas. Podemos generar semillas utilizando otros pasos de procesamiento, como identificando H-minima.
Combinando transformadas#
La transformada de cuenca se puede aplicar a cualquier imagen, pero tiene algunas aplicaciones particularmente interesantes cuando se aplica a una imagen que es un mapa de distancias.
Dividir objetos redondos#
Un mapa de distancia tiene máximos regionales siempre que un píxel de primer plano esté más lejos del fondo que cualquiera de sus vecinos.
Esto tiende a ocurrir hacia el centro de los objetos: particularmente objetos redondos que no contienen agujeros. Es importante destacar que los máximos regionales aún pueden estar presentes incluso si los “objetos redondos” están conectados entre sí en la imagen binaria utilizada para generar el mapa de distancia originalmente.
Esto significa que al aplicar una transformada de watershed a un mapa de distancias, podemos dividir estructuras «redondeadas» en imágenes binarias. El proceso es el siguiente:
Calcular el mapa de distancia de la imagen.
Invierte el mapa de distancias (por ejemplo, multiplícalo por -1), de modo que los picos se conviertan en valles.
Aplicar la transformación de watershed, a partir de los mínimos regionales del mapa de distancia invertido
Show code cell content
from skimage.morphology import disk, dilation
from skimage.segmentation import watershed
bw = np.zeros((75, 99), dtype=bool)
bw[37, 30] = True
bw[37, -30] = True
strel = disk(22)
bw = dilation(bw, strel)
im_dist = distance_transform_edt(bw)
lab = watershed(-im_dist, markers=None, mask=bw, watershed_line=True)
fig = create_figure(figsize=(8, 4))
show_image(bw, title='(A) Binary image', pos=131)
show_image(im_dist, title='(B) Distance map of (A)', pos=132)
show_image(lab > 0, title='(C) Watershed split of (B)', pos=133)
glue_fig('fig_morph_distance_split_small', fig)

Figura 121 Dividir objetos redondos usando las transformadas de distancia y watershed.#
Los objetos a dividir no tienen por qué ser perfectamente redondos. El único requisito es que haya máximos regionales claramente distintos en la transformada de distancia o, alternativamente, podemos definir semillas adecuadas utilizando otros pasos de procesamiento.
Show code cell content
from scipy.ndimage import distance_transform_edt, label
from skimage.color import label2rgb
from skimage import filters
im = load_image('blobs.gif')
bw = im < im.mean()
im_dist = distance_transform_edt(bw)
im_dist = np.round(im_dist)
# Defining the seeds is quite tricky, because there can be lots of tiny maxima
# Here, we use H-maxima to find only the larger maxima.
# We then still need to dilate them slightly to ensure maxima within the same
# blob are connected, to avoid having too many seeds.
from skimage.morphology import extrema
# bw_maxima = im_dist == ndimage.maximum_filter(im_dist, size=(5, 5))
bw_maxima = extrema.h_maxima(im_dist, 0.5)
bw_maxima = ndimage.binary_dilation(bw_maxima)
bw_maxima = bw_maxima & bw # Make sure we didn't dilate beyond the original binary mask
lab_seeds, n = label(bw_maxima)
fig = create_figure(figsize=(8, 6))
show_image(bw, title='(A) Binary image', pos=221)
show_image(im_dist, title='(B) Distance map from', pos=222)
show_image(label2rgb(lab_seeds, bg_label=0), title='(C) Seed labels from (B)', pos=223)
lab2 = watershed(-im_dist, markers=lab_seeds, mask=bw, watershed_line=True)
show_image(label2rgb(lab2, bg_label=0), title='(E) Watershed from (C, A)', pos=224)
plt.tight_layout()
glue_fig('fig_morph_distance_split', fig)

Figura 122 División de manchas fusionadas en función de la «redondez» utilizando las transformadas de distancia y watershed. Debido a que hay muchos máximos regionales pequeños en la transformada de distancia, aquí definimos semillas usando máximos H seguidos de una dilatación de 3 × 3 para evitar una división excesiva.#
Líneas de watershed
Al aplicar una transformada de watershed, a menudo es posible especificar si a las separaciones entre regiones se les asigna una de las etiquetas de región o se dejan como píxeles de fondo.
Aquí hemos mostrado las separaciones como píxeles de fondo. Esto es consistente con cómo funciona el comando de watershed predeterminado de ImageJ y también aclara las divisiones en las figuras que se muestran aquí. En el código Python que usa scikit-image, eso significa que estamos usando la opción watershed_lines=True.
Partición de imágenes con Voronoi#
Al calcular la transformación de distancia de una imagen binaria invertida se obtiene un mapa de distancia en el que cada píxel indica la distancia al objeto en primer plano más cercano.
Si aplicamos una transformación de cuenca a este mapa de distancia, utilizando los objetos en la imagen binaria como semillas, efectivamente dividimos la imagen en diferentes regiones según el objeto más cercano en la imagen binaria.
A esto a veces se le llama transformación de Voronoi de la imagen.
Show code cell content
from scipy.ndimage import distance_transform_edt, label
from skimage.segmentation import watershed
from skimage.color import label2rgb
im = load_image('blobs.gif')
bw = im < im.mean()
lab, n = label(bw)
im_dist_inv = distance_transform_edt(~bw)
bw_dilated = (im_dist_inv < 10)
fig = create_figure(figsize=(6, 6))
show_image(bw, title='(A) Binary image', pos=221)
show_image(label2rgb(lab, bg_label=0), title='(B) Seed labels from (A)', pos=222)
show_image(im_dist_inv, title='(C) Distance map from (A, inverted)', pos=223)
lab2 = watershed(im_dist_inv, lab, watershed_line=True)
show_image(label2rgb(lab2, bg_label=0), title='(D) Watershed from (B, C)', pos=224)
plt.tight_layout()
glue_fig('fig_morph_voronoi_expand', fig)

Figura 123 Expandir blobs para calcular la transformada de Voronoi de una imagen etiquetada, dividiéndola en diferentes regiones según el objeto semilla más cercano.#
Ampliando sin superposiciones#
Basándonos en la idea de Vononoi de la última sección, podemos expandir los objetos mismos de tal manera que no se superpongan.
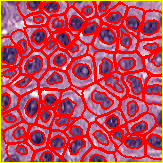
Figura 124 Detección de células de QuPath, basada en la detección de núcleos + expansión de watershed.#
Nuestro objetivo es dilatar cada objeto de la imagen 10 píxeles, pero sin fusionarlos. Si los objetos semilla están a menos de 20 píxeles de distancia, cada uno de ellos se expande la misma cantidad, hasta que se encuentran en el medio. Esta técnica se puede utilizar para aproximar un límite celular en función de los núcleos detectados mediante expansión utilizando una distancia fija.
En primer lugar, analizamos lo que no funciona. No podemos simplemente dilatar una imagen etiquetada con un filtro máximo, porque no hay nada que impida que las regiones se fusionen entre sí. Cuando las semillas están muy juntas, la etiqueta más alta «ganará» la carrera de expansión en todos los casos, dominando la producción.
Show code cell content
from scipy.ndimage import distance_transform_edt, label
from skimage.segmentation import watershed
from skimage.color import label2rgb
im = load_image('blobs.gif')
bw = im < im.mean()
lab, n = label(bw)
lab_dilated = morph.dilation(lab, disk(10))
fig = create_figure(figsize=(8, 6))
show_image(label2rgb(lab, bg_label=0), title='(A) Seed labels from (A)', pos=131)
show_image(label2rgb(lab_dilated, bg_label=0), title='(B) Seeds expanded by dilation', pos=132)
show_image(label2rgb(lab, bg_label=0), title='(C) Overlay of (A) and (B)', pos=133)
show_image(label2rgb(lab_dilated, bg_label=0), alpha=0.5, title='(C) Overlay of (A) and (B)')
plt.tight_layout()
glue_fig('fig_morph_bad_expand', fig)

Figura 125 Expandir blobs usando solo un filtro máximo. Este enfoque es demasiado simple; da como resultado etiquetas superpuestas y mucha confusión.#
En lugar de ello, debemos basarnos en el enfoque de Voronoi que se muestra en Figura 123. La única diferencia que debemos incorporar es que evitamos que la expansión de la cuenca crezca más allá de los 10 píxeles.
Afortunadamente, este criterio es fácil de establecer: nuestro mapa de distancias ya nos da la distancia a cada objeto semilla. Podemos establecer un umbral para definir una máscara binaria que indique dónde las regiones ya no deberían expandirse. Si actualizamos nuestra salida de cuenca para tener píxeles de fondo en las mismas ubicaciones donde nuestra máscara binaria tiene píxeles de fondo, habremos logrado una expansión restringida de 10 píxeles sin superposición.
Show code cell content
from scipy.ndimage import distance_transform_edt, label
from skimage.segmentation import watershed
from skimage.color import label2rgb
im = load_image('blobs.gif')
bw = im < im.mean()
lab, n = label(bw)
im_dist_inv = distance_transform_edt(~bw)
bw_dilated = (im_dist_inv < 10)
fig = create_figure(figsize=(8, 6))
show_image(bw, title='(A) Binary image', pos=231)
show_image(label2rgb(lab, bg_label=0), title='(B) Seed labels from (A)', pos=232)
show_image(im_dist_inv, title='(C) Distance map from (A, inverted)', pos=233)
show_image(bw_dilated, title='(D) Thresholded (C) < 10', pos=234)
lab2 = watershed(im_dist_inv, lab, mask=bw_dilated, watershed_line=True)
show_image(label2rgb(lab2, bg_label=0), title='(E) Masked watershed from (B, C, D)', pos=235)
lab2[~bw_dilated] = 0
show_image(label2rgb(lab, bg_label=0), title='(F) Expanded seeds', pos=236)
show_image(label2rgb(lab2, bg_label=0), alpha=0.5, title='(F) Expanded seeds')
plt.tight_layout()
glue_fig('fig_morph_distance_expand', fig)

Figura 126 Usar transformaciones de distancia y watershed para expandir regiones en una distancia fija, sin superposición. El resultado final (F) se obtiene utilizando información de todas las imágenes (A) - (E).#

