Operaciones puntuales#
Esquema del capítulo
Point operations o «operaciones puntuales» son operaciones matemáticas aplicadas a valores de píxeles individuales
Las operaciones puntuales se pueden realizar usando una imagen única, una imagen y una constante o dos imágenes del mismo tamaño
Algunas operaciones puntuales no lineales cambian las relaciones entre píxeles de una manera que puede ser útil para mejorar el contraste, pero deben usarse con precaución.
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Un paso utilizado para procesar una imagen de alguna manera se puede llamar operación.
Las operaciones más simples son operaciones puntuales, que actúan sobre píxeles individuales. Las operaciones puntuales cambian cada píxel de una manera que depende de su propio valor, pero no de dónde se encuentra en la imagen ni de los valores de otros píxeles. Esto contrasta con las operaciones vecinales, que calculan nuevos valores de píxeles en función de los valores de los píxeles cercanos.
Si bien no son inmediatamente muy glamorosas, las operaciones puntuales a menudo tienen roles indispensables en contextos más interesantes, por lo que es esencial saber cómo se usan y qué complicaciones buscar.
¿No es malo modificar píxeles?
La parte I enfatizó repetidamente que modificar píxeles es algo malo. Dado que el procesamiento de imágenes consiste en cambiar los valores de los píxeles, es hora de agregar un poco más de matices:
Modificar los valores de píxeles es malo, a menos que tengas una buena razón.
Una «buena razón» es algo que puedes justificar basándote en los datos de la imagen. Algo que podrías incluir con confianza en un artículo de revista que describa cómo analizaste tu imagen y convencer a un crítico de que fue una opción sensata.
También debes asegurarte de aplicar el procesamiento a un duplicado de la imagen y conservar el archivo original. De esa manera siempre podrás volver a los datos originales si es necesario.
Operaciones puntuales para imágenes individuales.#
Aritmética#
Los valores de píxeles son solo números. Cuando tenemos números, podemos hacer aritmética.
Por lo tanto, no debería sorprendernos que podamos tomar los valores de nuestros píxeles y cambiarlos sumando, restando, multiplicando o dividiendo por algún otro valor. Estas son las operaciones puntuales más simples.
Nos encontramos con esta idea antes cuando vimos que multiplicar nuestros valores de píxeles podría [aumentar el brillo] (sec_images_luts). Argumenté que esto era algo muy malo porque cambia nuestros datos. Nuestra mejor alternativa fue cambiar la LUT.
Sin embargo, a veces hay «buenas razones» para aplicar la aritmética a los valores de los píxeles, mejores que simplemente ajustar la apariencia. Ejemplos incluyen:
Restar un offset constante agregado por un microscopio antes de cuantificar las intensidades
Dividir por una constante para que puedas convertir la profundidad de bits sin recortar
Sin embargo, debemos tener en cuenta que no estamos tratando con matemáticas abstractas sino con bits y bytes. Lo que hace que la siguiente pregunta sea particularmente importante.
Supongamos que agregas una constante a cada píxel de la imagen. ¿Por qué restar la misma constante del resultado no te devolverá la imagen con la que empezaste?
Si agregas una constante que empuja los valores de píxeles fuera del rango admitido por la profundidad de bits (por ejemplo, 0–255 para 8 bits), entonces el resultado no cabe en la imagen. En su lugar, es probable que se recorte al valor más cercano posible. Restar la constante nuevamente no restaura el valor original.
Por ejemplo: 200 (valor original) + 100 (constante) → 255 (valor válido más cercano).
Pero luego 255 - 100 → 155.
En base a esto, un consejo importante para el procesamiento de imágenes es:
Convierta imágenes enteras a coma flotante antes de manipular píxeles
Es mucho menos probable que una imagen de coma flotante de 32 bits (o incluso 64 bits) sufra errores debido al recorte y al redondeo. Por lo tanto, el primer paso de cualquier procesamiento de imágenes suele ser convertir la imagen a un formato de coma flotante.
Consulte Tipos y profundidad de bits para obtener más detalles.
Inversión de imagen#
Invertir una imagen implica efectivamente «invertir» las intensidades: hacer que los valores más altos sean más bajos y los valores más bajos más altos.
En el caso de imágenes de 8 bits, los valores de píxeles invertidos se pueden calcular fácilmente restando los valores originales del máximo posible, es decir, de 255.
¿Por qué es útil la inversión?
Supongamos que tienes una buena estrategia diseñada para detectar estructuras brillantes, pero no te funciona porque tus imágenes contienen estructuras oscuras. Si primero inviertes tus imágenes, las estructuras se vuelven brillantes y tu estrategia de detección ahora podría tener éxito.
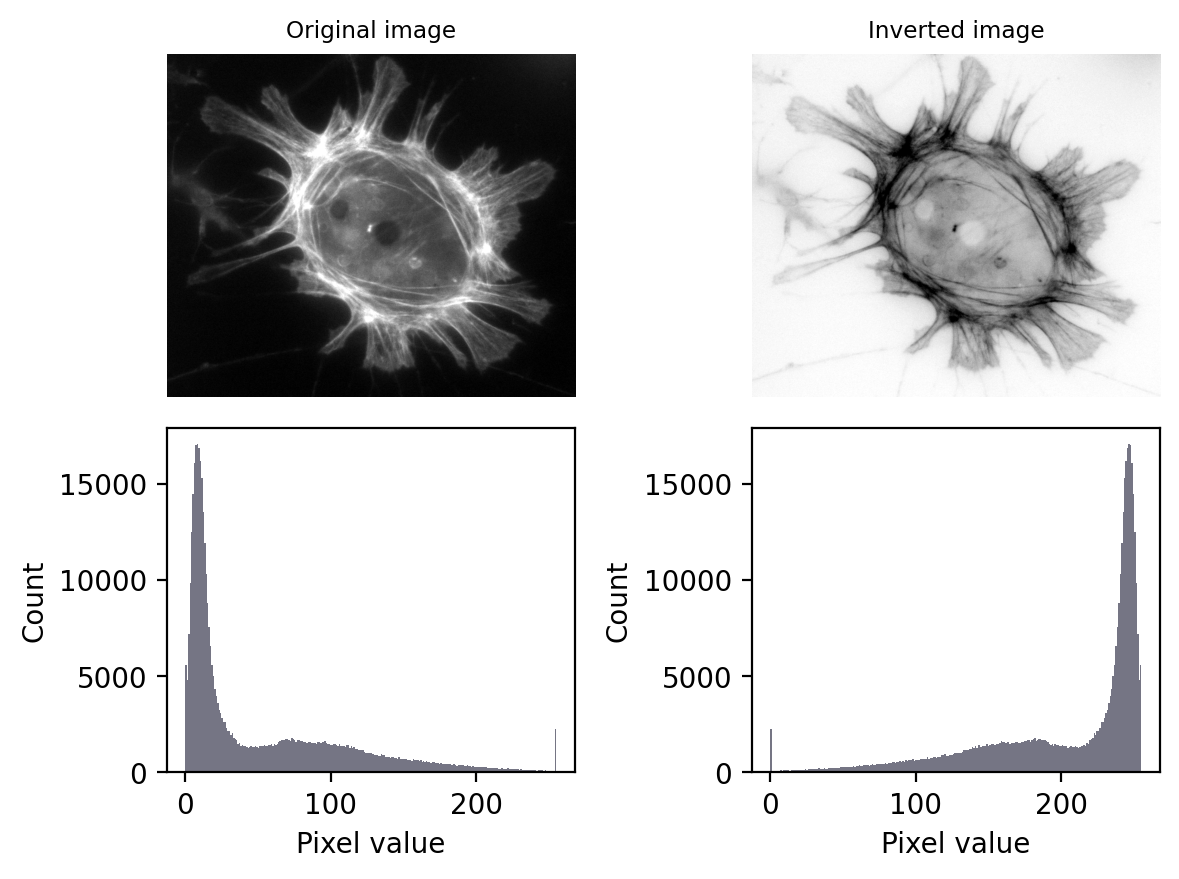
Figura 58 El efecto de la imagen y la inversión LUT. Ten en cuenta que cada histograma parece ser una imagen de espejo del otro. Además, la imagen está recortada (lo siento).#
Definición del “máximo” al invertir una imagen
Invertir una imagen de 8 bits (entero sin signo) generalmente significa restar todos los valores de píxeles de 255, porque 255 es el máximo admitido por el tipo de imagen y la profundidad de bits.
El «máximo» no siempre se define de esta manera. Para una imagen de 32 o 64 bits (ya sea entera o de coma flotante), el valor máximo posible es enorme, y usarlo daría como resultado valores de píxeles excesivamente grandes. Por lo tanto, el «máximo» generalmente se define de alguna otra manera en lugar de basarse en el tipo de imagen, como tomando el valor máximo de píxeles encontrado dentro de la imagen.
Como no me gusta dejar que el software decida qué máximo usar, a menudo hago trampa: multiplico los píxeles por -1 (asegurándome de que la imagen sea de coma flotante). Esto conserva las propiedades clave de la inversión de imágenes: invierte los valores altos y bajos, conservando al mismo tiempo todas las diferencias relativas entre valores.
Mejora del contraste no lineal#
Con operaciones aritméticas cambiamos los valores de los píxeles, de manera útil o no, pero (asumiendo que no hemos recortado nuestra imagen en el proceso) lo hemos hecho de forma lineal. A lo sumo haría falta otra multiplicación y/o suma para regresar a donde estábamos. Debido a que existe una relación similar entre los valores de píxeles, también podríamos ajustar el LUT de brillo y contraste para que no parezca como si no hubiéramos hecho nada en absoluto.
Las operaciones puntuales no lineales se diferencian en que afectan los valores relativos de manera diferente dependiendo de cuáles eran en primer lugar. Estos son particularmente útiles para mejorar el contraste.
Cuando cambiamos el brillo y el contraste en Tablas de búsqueda, estábamos haciendo ajustes lineales. Para una LUT en escala de grises, esto significa que elegimos el valor de píxel para mostrar como negro y el valor de píxel para mostrar como blanco, con cada valor intermedio asignado a un tono de gris a lo largo de una línea recta ({numref} fig-nonlinear_contrastA).
Opcionalmente, podríamos usar valores de mapeo no lineal entre valores y tonos de gris, pero la mayoría de programas de software no facilitan el cambio de LUT de formas suficientemente complicadas. Un enfoque más sencillo es duplicar la imagen y aplicar cualquier ajuste no lineal a los valores de los píxeles y luego asignarlos a tonos de gris de la forma habitual (lineal).
Las transformaciones no lineales comunes consisten en tomar el logaritmo del valor del píxel (Figura 59B), o reemplazar cada valor \(p\) con \(p^\gamma\) donde \( \gamma\) es el parámetro gamma que se puede ajustar dependiendo del resultado deseado (Figura 59B-D).
Show code cell source
"""
Visualizing non-linear transforms and their impact on a ramp profile plot.
"""
fig = plt.figure(figsize=(12, 4))
# See ImageJ implementation at
# https://github.com/imagej/imagej1/blob/a0d335d1df4e4c0b4fc12c71ecfbb889d4c62e62/ij/process/ImageProcessor.java#L953
# Create a linear ramp of pixel values from 0-255
# This simulates an 8-bit ramp image
# (although we'll do the calculations in 32-bit)
ramp = np.tile(np.linspace(0, 255, num=256, dtype=np.float32), (64, 1))
plot_args = dict(xlabel='Original value', ylabel='New value', color=(0.6, 0.6, 0.8), linewidth=2)
# Show main plot (linear ramp)
show_image(ramp, cmap=lut, title='(A) Original', pos=241)
show_plot(ramp[0, :], pos=245, **plot_args)
plt.xticks(np.arange(0, 255, 50))
# Apply log transform
ramp_log = np.log(np.maximum(ramp, 1.0))*255/np.log(255)
show_image(ramp_log, cmap=lut, title='(B) Log', pos=242)
show_plot(ramp_log[0, :], pos=246, **plot_args)
plt.xticks(np.arange(0, 255, 50))
# Apply gamma transform (gamma = 0.5)
ramp_gamma05 = np.power(ramp/255, 0.5)*255
show_image(ramp_gamma05, cmap=lut, title='(C) Gamma 0.5', pos=243)
show_plot(ramp_gamma05[0, :], pos=247, **plot_args)
plt.xticks(np.arange(0, 255, 50))
# Apply gamma transform (gamma = 2.0)
ramp_gamma2 = np.power(ramp/255, 2)*255
show_image(ramp_gamma2, cmap=lut, title='(D) Gamma 2.0', pos=244)
show_plot(ramp_gamma2[0, :], pos=248, **plot_args)
plt.xticks(np.arange(0, 255, 50))
# plt.subplots_adjust(wspace=0.4)
plt.tight_layout()
glue_fig("fig_points_gamma_ramp", fig)
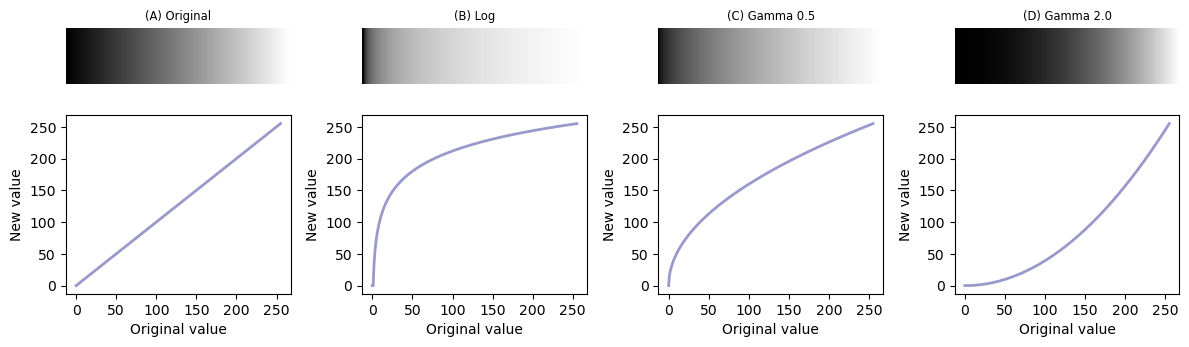
Figura 59 Transformaciones no lineales aplicadas a una imagen de “rampa” simple, que consta de valores de píxeles que aumentan linealmente. Reemplazar cada píxel con su valor log o gamma ajustado tiene el efecto de comprimir las intensidades más bajas o más altas para liberar más niveles de gris para los demás. Ten en cuenta que aquí asumimos una imagen de entrada de 8 bits y hemos incorporado algunos cambios de escala necesarios para una salida de 8 bits (según el enfoque utilizado por ImageJ).#
Si todo esto suena dudoso e incómodo, ten la seguridad de que lo es: es mejor evitar las transformaciones no lineales siempre que sea posible.
Sin embargo, hay un escenario en el que realmente pueden ayudar: mostrar una imagen con un alto rango dinámico, es decir, una gran diferencia entre los valores de píxeles más grandes y más pequeños.
Figura 60 muestra esto en acción. Aquí, los valores de píxeles asociados con el personaje principal son todos bastante altos. Sin embargo, los valores asociados a la figura fantasmal son todos muy bajos. No hay configuraciones de contraste lineal con una LUT en escala de grises estándar que permitan ver ambas figuras a detalle, simultáneamente. Sin embargo, las transformaciones log o gamma lo hacen posible.
Show code cell source
"""
Comparing transforms for an image with a high dynamic range.
"""
fig = create_figure(figsize=(8, 6))
# See ImageJ implementation at
# https://github.com/imagej/imagej1/blob/a0d335d1df4e4c0b4fc12c71ecfbb889d4c62e62/ij/process/ImageProcessor.java#L953
im = load_image('spooked.png')
# Show original image
show_image(im, vmin=0, vmax=255, title="Original image", pos=221)
# Set display range (linear contrast adjustment)
# (This has to be extremely stark to show the background details)
show_image(im, vmin=0, vmax=10, title="Linear contrast", pos=222)
# Apply gamma transform
im_gamma05 = np.power(im/255, 0.4)*255
show_image(im_gamma05, vmin=0, vmax=255, title="Gamma adjusted", pos=223)
# Apply log transform
im_log = np.log(np.maximum(im, 1.0))*255/np.log(255)
show_image(im_log, vmin=0, vmax=255, title="Log transform", pos=224)
glue_fig("fig_points_gamma", fig)
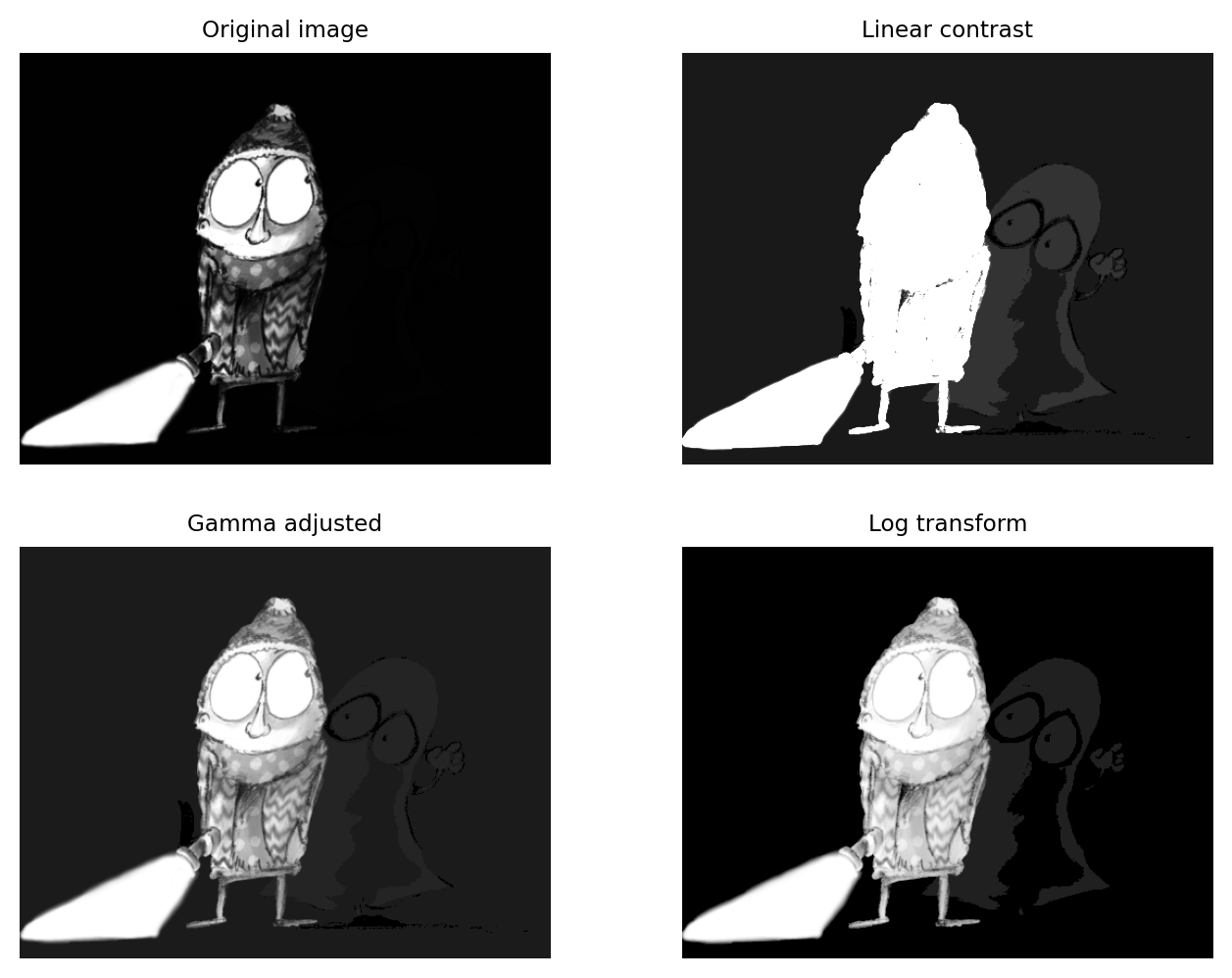
Figura 60 La aplicación de mejora de contraste no lineal a una imagen con una amplia gama de valores. (Fila superior) En la imagen original, no es posible ver detalles tanto en primer plano como en fondo simultáneamente. (Fila inferior) Dos ejemplos de técnicas no lineales que hacen que los detalles sean visibles en toda la imagen.#
¡Evita la manipulación de imágenes!
Al crear figuras para publicación, cambiar el contraste de alguna manera lineal normalmente se considera correcto (suponiendo que no se haya hecho con mala intención para hacer imposible discernir algunos detalles inconvenientes que socavan la investigación).
Pero si se utilizan operaciones no lineales, ¡siempre deben anotarse en la leyenda de la figura!
Esto se debe a que, aunque las operaciones no lineales pueden ser muy útiles cuando se usan con cuidado, también pueden inducir a error fácilmente, exagerando o subestimando las diferencias de brillo.
Operaciones puntuales y múltiples imágenes.#
En lugar de aplicar la aritmética usando una imagen y una constante, también podríamos usar dos imágenes del mismo tamaño. Estos se pueden sumar, restar, multiplicar o dividir fácilmente aplicando las operaciones a los píxeles correspondientes.
Esta es una técnica que se utiliza todo el tiempo en el procesamiento de imágenes. Las aplicaciones incluyen:
restando diferentes fondos
calculo de relaciones de intensidad
crear mascaras en regiones
y mucho más…
Combinaremos imágenes de esta manera en el resto del manual.
En las dos imágenes de 32 bits que se muestran aquí, los píxeles blancos tienen valores de uno y los píxeles negros tienen valores de cero (los píxeles grises tienen valores intermedios).
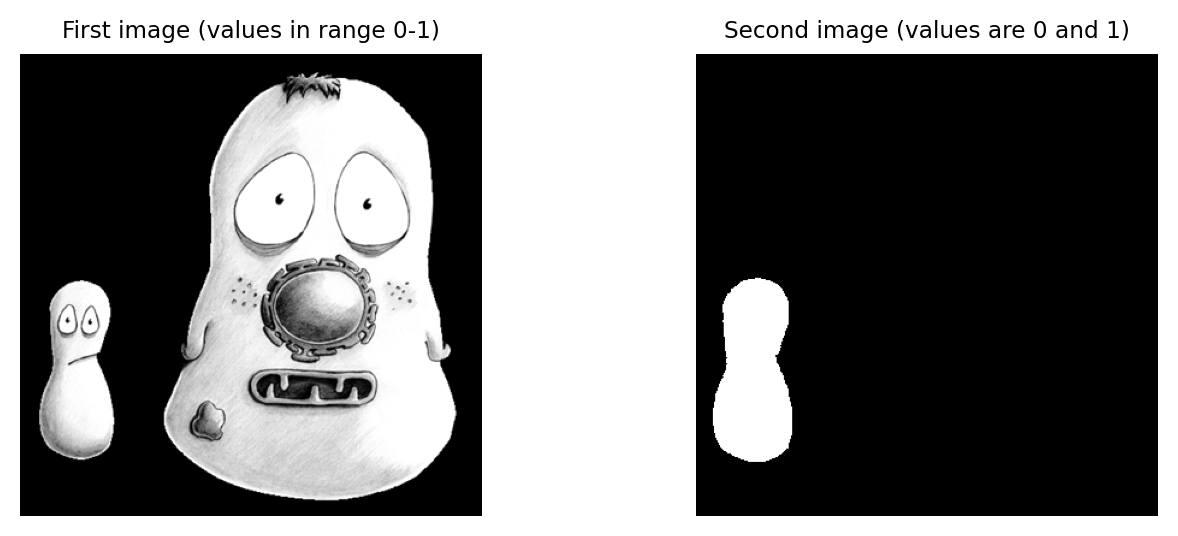
¿Cuál sería el resultado de multiplicar las imágenes? ¿Y cuál sería el resultado de dividir la imagen de la izquierda por la imagen de la derecha?
Multiplicar las imágenes efectivamente da como resultado que todo lo que esté fuera de la región blanca en la imagen derecha se elimine de la imagen izquierda (es decir, se establezca en cero).

La división tiene un efecto similar, excepto que en lugar de convertirse en cero, los píxeles enmascarados tomarán uno de tres resultados, dependiendo del valor del píxel original en la imagen de la izquierda:
si fue positivo, el resultado es \(+\infty\) (aquí se muestra en amarillo)
si fue negativo, el resultado es \(-\infty\)
si fue cero, el resultado es
NaN(“no es un número” - indica que 0/0 no está definido; se muestra aquí en rojo)
Estos son valores especiales que pueden estar contenidos en imágenes de punto flotante, pero no en imágenes con tipos enteros.
Show code cell source
"""
Adding noise to an image.
"""
# Load a sample image, normalize between 0 and 5
im = load_image('happy_cell.tif')
im = im - im.min()
im = im / im.max() * 5
# Create a random number generator - always good to seed this,
# to keep the randomness predictable each time we run the code...
rng = np.random.default_rng(100)
# Create a normally-distributed random value for every pixel
# Mean = 0, Std. dev. 1
im_noise = rng.normal(size=im.shape)
# The image we can acquire has the noise added
im_possible = im + im_noise
# Show images
fig = create_figure(figsize=(8, 4))
show_image(im, title="(A) Ideal image", pos=131)
show_image(im_noise, title="(B) Random noise", pos=132)
show_image(im_possible, title="(C) Acquired image", pos=133)
glue_fig("fig_points_noise_added", fig)
Agregando ruido
Las imágenes de fluorescencia son invariablemente ruidosas. El ruido aparece como granulosidad en toda la imagen, lo que puede considerarse que surge de un valor de ruido aleatorio (positivo o negativo) que se agrega a cada píxel.
Esto equivale a añadir una “imagen de ruido” separada a la imagen más limpia inexistente que preferiríamos haber grabado. Si conociéramos los píxeles de la imagen de ruido, simplemente podríamos restarlos para obtener el resultado limpio, pero, en la práctica, su aleatoriedad significa que no los conocemos.

Figura 61 Simulación de una adquisición de imágenes imperfecta añadiendo ruido a una imagen «ideal».#
A pesar de que el ruido no es deseable, agregar imágenes de ruido puede resultar extremadamente útil al desarrollar y validar métodos de análisis de imágenes.
Podemos usarlo para crear simulaciones en las que el ruido se comporta estadísticamente como el ruido real y agregarlo a imágenes limpias. Usando estas simulaciones podemos descubrir, por ejemplo, cómo los pasos de procesamiento o los cambios durante la adquisición afectarán o reducirán el ruido, o qué tan sensibles son nuestras estrategias de medición a los cambios en la calidad de la imagen (consulte {ref} chap_filters, Ruido y chap_macro_simulated).

