ImageJ: Filtros#
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
La mayoría de los filtros que hemos considerado están disponibles a través del submenú . Esta sección agrega un poco más de información sobre su implementación en ImageJ y plantea algunas preguntas.
Filtros lineales#
Filtros medios#
La forma más sencilla de aplicar un filtro medio de 3 × 3 en ImageJ es mediante el comando . El hecho de que el atajo sea Shift+S casi puede hacer que esto sea demasiado fácil, ya que me encuentro suavizando accidentalmente cuando realmente quería guardar mi imagen. Ten cuidado.
Para aplicar filtros de media más grandes, el comando es . Utiliza vecindades aproximadamente circulares y el tamaño de la vecindad se ajusta eligiendo un valor de Radius. El comando muestra las vecindades utilizadas para diferentes valores de Radius. Si eliges Radius = 1, obtendrás un filtro de 3×3, y los mismos resultados que usando .

Filtros Gaussianos#
es el comando que implementa un filtro Gaussiano.
En el caso de que desees un filtro Gaussiano que no sea isotrópico (es decir, que tenga un tamaño diferente en diferentes dimensiones), se puede utilizar
Aunque no se recomienda realmente, la máscara de desenfoque está disponible a través de .
Diferencia de Gaussianos
Actualmente no existe un comando directo en ImageJ para implementar la diferencia de filtrado Gaussiano, sino que los pasos deben unirse con la duplicación y resta de imágenes. Sin embargo, Diferencia de Gaussianos describe cómo generar una macro para el filtrado por diferencia de Gaussianos (DoG).
Filtros lineales personalizados#
permite definir cualquier filtro lineal personalizado ingresando los valores de los coeficientes deseados, separados por espacios y ordenados en filas y columnas. Si seleccionas {guilabel} Normalize Kernel, entonces los coeficientes se escalan para que sumen 1, dividiéndolos por la suma de todos los coeficientes, a menos que la suma sea 0, en cuyo caso solicitar la normalización no hace nada.
Al definir un núcleo (kernel) de filtro n_×_n con , ImageJ insiste en que n es un número impar. ¿Por qué?
Si n es un número impar, el filtro tiene un píxel central claro. Esto hace posible centrar el núcleo (kernel) del filtro en un píxel de la imagen.
Predice qué sucede cuando convolucionas una imagen usando un filtro que consta de un único coeficiente con un valor -1 en los siguientes casos:
Normalize Kernel está marcado
Tienes una imagen de 32 bits, Normalize Kernel no está marcado
Tienes una imagen de 8 bits, Normalize Kernel no está marcado
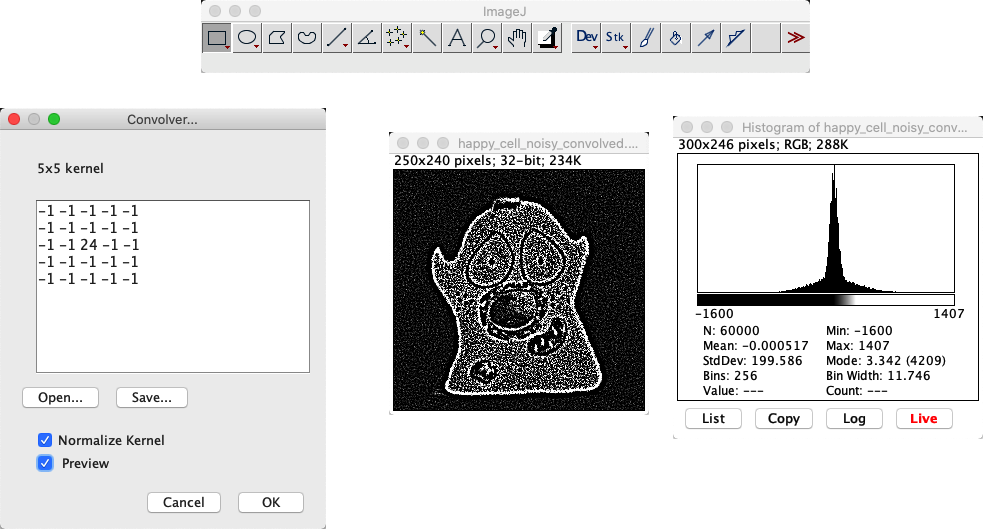
Los resultados de convolucionar con un único coeficiente -1 en diferentes circunstancias:
Normalize Kernel está marcado: No sucede nada en absoluto. La normalización hace que el filtro sea solo un 1… y la convolución con un solo 1 deja la imagen sin cambios.
Tienes una imagen de 32 bits (Normalize Kernel sin marcar): Los valores de píxeles se vuelven negativos y la imagen parece invertida.
Tienes una imagen de 8 bits (Normalize Kernel sin marcar): Los valores de píxeles se volverían negativos, pero luego no se pueden almacenar en un formato entero de 8 bits sin signo. Por lo tanto, todos los píxeles simplemente se recortan a cero.
Utilizando cualquier imagen, determine cuál de los métodos para tratar los límites que se muestran en Figura 86 es utilizado por el comando {menuselection} Convolve...
Nota: Esto requiere un poco de creatividad. Sin duda será útil utilizar una imagen con alguna variación en el límite de la imagen. Usé .
La replicación de píxeles de límite es el método predeterminado utilizado por en ImageJ (aunque otros plugins de filtrado de diferentes autores pueden usar diferentes métodos).
Mi enfoque para probar esto implicó usar con un filtro que consiste en un 1 seguido de muchos ceros (por ejemplo, 1 0 0 0 0 0 0 0 0 0 0 0 0...). Básicamente, esto desplaza la imagen hacia la derecha, mostrando todo lo que está fuera del límite de la imagen.
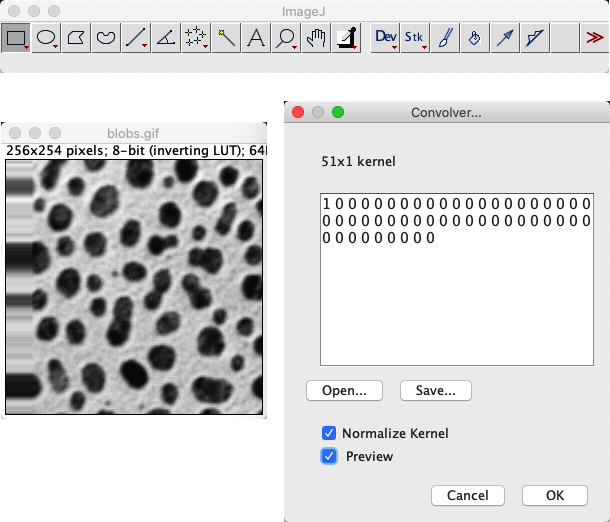

Figura 100 Magnitud del gradiente#
Practica usando los comandos que hemos visto hasta ahora determinando la magnitud del gradiente de una imagen, como se describe aquí.
Necesitarás usar
Varios comandos en el submenú
Algo más que hemos usado antes… posiblemente
Si necesitas una imagen de muestra, puedes usar . (¡Asegúrate de prestar atención a la profundidad de bits!)
El proceso para calcular la magnitud del gradiente es:
Convierte la imagen a 32 bits (si aún no es de 32 bits)
Duplicar la imagen
Convoluciona una copia de la imagen con el filtro de gradiente horizontal y otra con el vertical (es decir, coeficientes
-1 0 1organizados como una fila o columna)Calcula el cuadrado de ambas imágenes ()
Utiliza la calculadora de imágenes para sumar las imágenes.
Calcula la raíz cuadrada de la imagen resultante ()
Aquí hay una macro que implementa estos pasos:
run("32-bit");
id1 = getImageID()
run("Duplicate...", " ");
id2 = getImageID();
run("Convolve...", "text1=[-1 0 1\n] normalize");
run("Square");
selectImage(id1);
run("Convolve...", "text1=-1\n0\n1\n normalize");
run("Square");
imageCalculator("Add create", id1, id2);
run("Square Root");
La convolución da como resultado valores negativos, por lo que es necesaria la conversión a 32 bits.
Nota: Esto es (casi) lo que hace el comando , excepto que los filtros de gradiente son ligeramente diferentes.

Figura 101 El LUT de los “bordes”#
ImageJ tiene una LUT llamada bordes en . Aplicado a , hace un trabajo bastante bueno al resaltar los bordes, sin cambiar los píxeles en absoluto.
¿Como funciona? ¿Aplica un filtro?
La LUT muestra la mayoría de los valores de píxeles altos y bajos en negro, y utiliza tonos de gris más claros solo para un pequeño rango de valores intermedios (consulte ). En cualquier imagen con una buena separación entre los píxeles de fondo y de primer plano, pero que aún tenga una transición algo suave entre ellos, esto significa que todo, excepto los bordes, puede aparecer negro.
Todo esto se logra mediante una LUT: no se dañaron píxeles ni se aplicó ningún filtrado.
Filtros no lineales#
Filtros de clasificación#
Los principales filtros de clasificación se encuentran exactamente donde podría esperarlos:
ImageJ utiliza vecindades circulares con sus filtros de clasificación integrados, de forma similar a cómo se implementan los filtros medios. Volveremos a encontrarnos con estos filtros en Operaciones morfológicas.
Eliminando valores atípicos#
Figura 88 muestra que el filtrado mediano es mucho mejor que el filtrado medio para eliminar valores atípicos. Podríamos encontrarnos con esto si algo en el microscopio no funciona como se esperaba o si el ruido oscuro es un problema, pero por lo demás esperamos que el ruido en las imágenes de microscopía de fluorescencia produzca pocos valores realmente extremos (consulte {ref} chap_formation_noise).
Sin embargo, proporciona una alternativa si hay valores brillantes aislados. Este es un filtro no lineal que inserta valores medianos solo cuando se encuentra un píxel que está más alejado de la mediana local que algún umbral ajustable.
Es por tanto como un filtro mediano más selectivo que sólo modificará la imagen en los píxeles donde se considere realmente necesario.

