Ruido#
Esquema del capítulo
Existen dos tipos principales de ruido en microscopía de fluorescencia: **ruido fotónico y ruido de lectura
**El ruido fotónico depende de la señal y varía a lo largo de la imagen.
**El ruido de lectura es independiente de la señal y depende del detector.
Detectar más fotones reduce el impacto de ambos tipos de ruido
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Es razonable esperar que una imagen de microscopía sin ruido tenga un aspecto agradablemente lisa, entre otras cosas porque la convolución con la PSF tiene un efecto de desenfoque que suaviza cualquier transición brusca. Sin embargo, en la práctica, las imágenes en bruto de microscopía de fluorescencia no son “lisas”. Siempre están, en mayor o menor medida, corrompidas por el ruido. Éste aparece como un «grano» aleatorio en toda la imagen, que a menudo es lo suficientemente fuerte como para ocultar los detalles.
En este capítulo se analiza la naturaleza del ruido, de dónde procede y qué se puede hacer al respecto. Antes de empezar, puede ser útil saber que la lección principal de este capítulo para el microscopista activo es simplemente:
Truco
Si quieres reducir el ruido, necesitas detectar más fotones
Esta orientación general se aplica en la inmensa mayoría de los casos cuando un microscopio de buena calidad funciona correctamente. No obstante, puede ser útil conocer un poco más a detalle por qué y qué hacer si no es posible detectar más fotones.
Fondo#
Show code cell content
"""
Visualize an image with/without noise.
The point is that noise comprises random positive/negative values,
usually with a predictable distribution.
(Of course, in the simulation we can make sure that's the case...
but real-world investigations support the basis of these simulations)
"""
# Load image & normalize between 0 and 1
im = load_image('happy_cell.tif').astype(np.float32)
im = im - im.min()
im = im / im.max()
# Adjust the intensities a bit.
# This allows us to balance the brightness signal and the background,
# which helps because for very low signals Poisson noise looks weirder -
# and right now we don't want to be distracted by odd-looking histograms.
# We'll cover that later.
background = 40
max_signal = 100
im = background + im * (max_signal - background)
# Blur (to simulate point spread function)
sigma = 2
im = ndimage.gaussian_filter(im, sigma)
# Add Poisson noise (for realism)
rng = np.random.default_rng(100)
im_noisy = rng.poisson(im)
# Compute the difference between the noisy image & ideal image
im_diff = im_noisy - im
# Show images
fig = create_figure(figsize=(8, 1.8))
show_image(im_noisy, title='(A) Noisy image', pos=141)
show_image(im, title='(B) Noise-free (blurred) image', pos=142)
show_image(im_diff, title='(C) Result of (A) - (B)', clip_percentile=1, pos=143)
show_histogram(im_diff.flatten(), xlabel=None, ylabel=None, title='(D) Histogram of (A) - (B)', pos=144)
plt.xticks([])
plt.yticks([])
# plt.tight_layout()
glue_fig('fig_noise_demo', fig)

Figura 142 Ilustración de la diferencia entre una imagen con ruido que podemos grabar (A), y la imagen sin ruido que preferiríamos (B). El «ruido» en sí es lo que quedaría si restáramos una de la otra (C). El histograma en (D) se asemeja a una distribución normal (es decir, Gaussiana) y muestra que el ruido consiste en valores positivos y negativos, con una media de 0.#
En general, podemos suponer que el ruido en las imágenes de microscopía de fluorescencia tiene las tres características siguientes, ilustradas en Figura 142:
El ruido es aleatorio – Para cualquier píxel, el ruido es un número aleatorio positivo o negativo añadido al «valor verdadero» que debería tener el píxel.
El ruido es independiente en cada píxel – El valor del ruido en cualquier píxel no depende de dónde esté el píxel, o de cuál sea el ruido en cualquier otro píxel.
El ruido sigue una distribución particular – Cada valor de ruido puede verse como una variable aleatoria extraída de una distribución particular. Si tenemos suficientes valores de ruido, su histograma se parecería a un gráfico de la distribución [^fn_1].
Hay muchas distribuciones de ruido posibles, pero sólo tenemos que considerar los casos Poisson y Gaussiano. Sea cual sea, el parámetro de distribución más interesante para nosotros es la desviación estándar. Suponiendo que todo lo demás permanezca igual, si la desviación estándar del ruido es mayor, la imagen tendrá peor aspecto (Figura 143).
Show code cell content
"""
Demonstrate that noise with a higher standard deviation makes an image
look worse, if all else stays the same (i.e. lower signal-to-noise ratio).
"""
# Load image
im = load_image('happy_cell.tif').astype(np.float32)
# Add noise with different standard deivations
rng = np.random.default_rng(200)
im_noise_5 = im + rng.normal(size=im.shape) * 5
im_noise_10 = im + rng.normal(size=im.shape) * 10
im_noise_20 = im + rng.normal(size=im.shape) * 20
fig = create_figure(figsize=(8, 4))
show_image(im_noise_5, title='(A) Std. dev. 5', clip_percentile=1, pos=231)
show_image(im_noise_10, title='(B) Std. dev. 10', clip_percentile=1, pos=232)
show_image(im_noise_20, title='(C) Std. dev. 20', clip_percentile=1, pos=233)
# Easier to show histograms with same settings in a loop
pos = 234
for im_noise in [im_noise_5, im_noise_10, im_noise_20]:
show_histogram(im_noise.flatten(), pos=pos)
plt.xlim([-50, 110])
plt.ylim([0, 3000])
pos += 1
plt.tight_layout()
glue_fig('fig_gaussian_hists', fig)
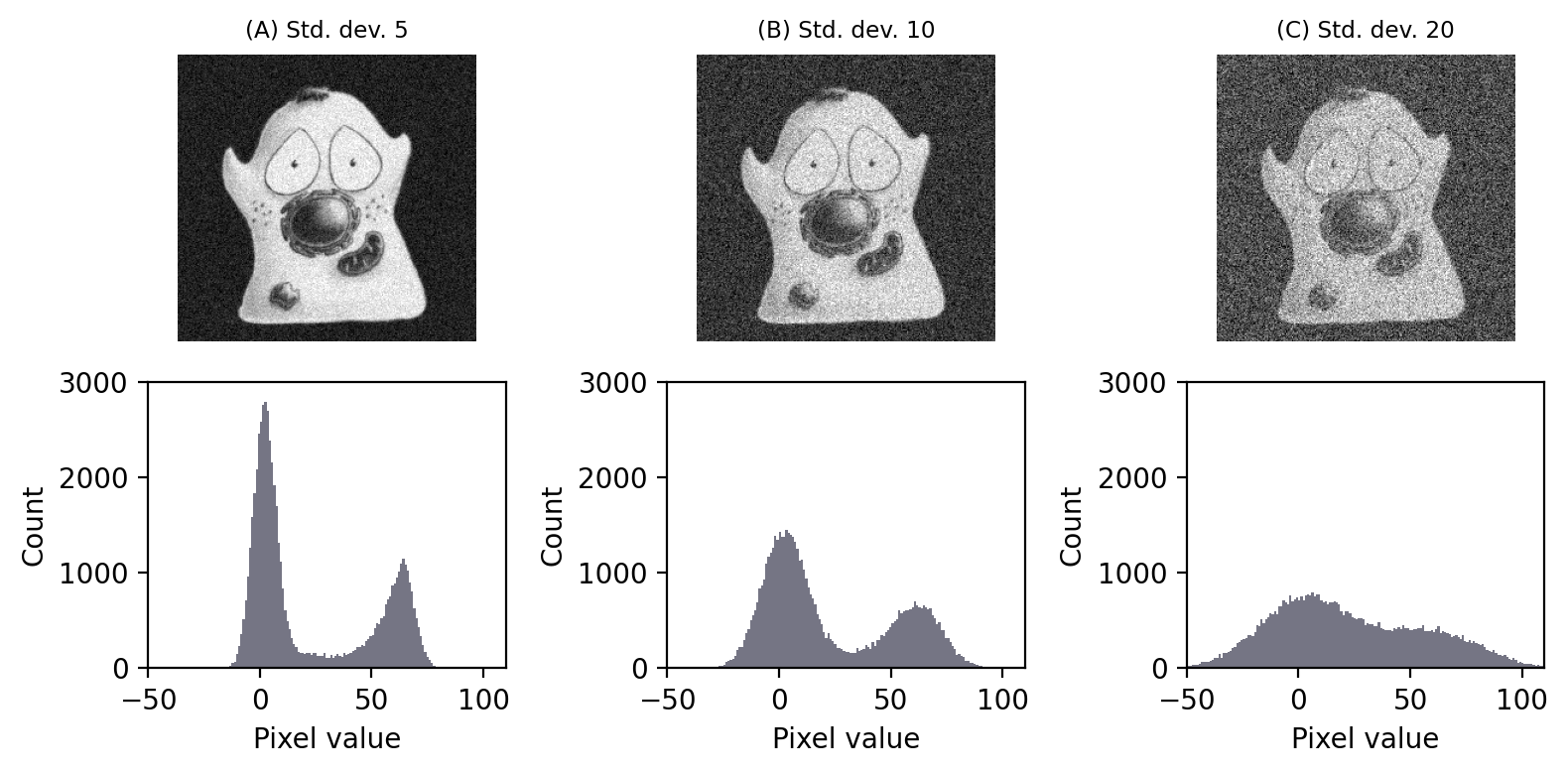
Figura 143 Ruido Gaussiano con diferentes desviaciones estándar añadido a una imagen. El ruido con una desviación estándar más alta tiene un efecto peor cuando se añade a una imagen. Su impacto puede verse en el histograma, ya que la distribución de los píxeles del primer plano y del fondo se sobreponen más – lo que es problemático para cosas como thresholding.#
La razón por la que consideraremos dos distribuciones es que hay dos tipos principales de ruido de los que debemos preocuparnos:
Ruido fotónico, procedente de la emisión (y detección) de la propia luz. Éste sigue una distribución de Poisson, para la cual la desviación estándar cambia con el brillo local de la imagen.
Ruido de lectura, debido a las imprecisiones en la cuantificación del número de fotones detectados. Sigue una distribución Gaussiana, para la que la desviación típica es la misma en toda la imagen.
Por lo tanto, el ruido en la imagen es realmente el resultado de sumar dos [^fn_2] componentes aleatorios separados. En otras palabras, para obtener el valor de cualquier píxel \(P\) hay que calcular la suma del valor «verdadero» (sin ruido) \(T\), un valor de ruido fotónico aleatorio \(N_p\), y un valor de ruido de lectura aleatorio \(N_r\), es decir
En este caso, tenemos \(P\) en la imagen pero queremos \(T\). Por desgracia, no sabemos con precisión cuáles son los valores aleatorios \(N_p\) y \(N_r\).
Por último, algunas matemáticas útiles:
Supongamos que sumamos dos valores aleatorios ruidosos. Ambos son independientes y proceden de distribuciones (Gaussiana o Poisson) con desviaciones típicas \(\sigma_1\) y \(\sigma_2\). El resultado es un tercer valor aleatorio, extraído de una distribución con una desviación típica \(\sqrt{\sigma_1^2 + \sigma_2^2}\).
Si multiplicamos un valor ruidoso de una distribución con una desviación típica \(\sigma_1\) por \(k\), el resultado es ruido de una distribución con una desviación típica \(k\sigma_1\).
Estos son los datos más importantes sobre el ruido, sobre los que se construye el resto de este capítulo. Empezaremos con el ruido Gaussiano porque es más fácil trabajar con él, se encuentra en muchas aplicaciones y está ampliamente estudiado en la literatura sobre procesamiento de imágenes. Sin embargo, en la mayoría de las imágenes de fluorescencia, el ruido fotónico es el factor más importante. Afortunadamente, existe una estrecha relación entre el ruido Gaussiano y el de Poisson, e incluso es posible convertir este último para que se comporte como el primero.
Ruido Gaussiano#
El ruido Gaussiano es un problema común en las imágenes de fluorescencia adquiridas con una cámara CCD (véase Microscopios y detectores). Surge en la fase de cuantificación del número de fotones detectados en cada píxel. Cuantificar los fotones es difícil de hacer con total precisión, y es probable que el resultado sea erróneo en al menos unos pocos fotones. Este error es el ruido de lectura.
El ruido de lectura sigue normalmente una distribución Gaussiana y tiene una media de cero: esto implica que existe la misma probabilidad de sobre-estimar o subestimar el número de fotones. Además, de acuerdo con las propiedades de las distribuciones Gaussianas, deberíamos esperar que alrededor del ~68% de las mediciones tengan una desviación estándar de ±1 respecto al valor real sin ruido de lectura. Si un detector tiene una desviación estándar de ruido de lectura baja, esto es bueno: significa que el error debería ser pequeño.
Relación señal/ruido (SNR)#
Se dice que el ruido de lectura es independiente de la señal: su desviación estándar es constante y no depende del número de fotones cuantificados. Sin embargo, la medida en que el ruido de lectura es un problema probablemente depende del número de fotones. Por ejemplo, si hemos detectado 20 fotones, una desviación estándar del ruido de 10 fotones es enorme; si hemos detectado 10 000 fotones, probablemente no sea tan importante.
Una mejor forma de evaluar el ruido de una imagen es entonces la relación entre el componente interesante de cada píxel (llamado señal, que es aquí lo que idealmente detectaríamos en términos de fotones) y la desviación estándar del ruido, lo que se conoce como Relación señal/ruido [^fn_3]:
Calcula la SNR en los siguientes casos:
Detectamos una media de 10 fotones, desviación estándar del ruido de lectura 1 fotón
Detectamos una media de 100 fotones, desviación estándar del ruido de lectura 10 fotones
Detectamos una media de 1000 fotones, desviación estándar del ruido de lectura 10 fotones
A efectos de esta pregunta, debes suponer que el ruido de lectura es el único ruido presente (ignora el ruido de fotones).
Detectamos una media de 10 fotones, desviación estándar del ruido de lectura. 1 fotón: SNR = 10
Detectamos una media de 100 fotones, desviación típica del ruido de lectura. 10 fotones: SNR = 10
Detectamos una media de 1000 fotones, desviación típica del ruido de lectura. 10 fotones: SNR = 100
El ruido nos causa un grado similar de incertidumbre en los dos primeros casos. En el tercer caso, es probable que el ruido sea menos problemático: las SNR más altas son buenas.
Explorar el ruido
Creo que la mejor forma de aprender sobre el ruido es crear imágenes de simulación y explorar sus propiedades haciendo y probando predicciones.
Las figuras de este capítulo se han generado utilizando este tipo de simulaciones en Python. Si deseas hacer algo similar en ImageJ, puedes añadir ruido Gaussiano con una desviación estándar fija a cualquier imagen utilizando .
Si es necesario, puedes crear una imagen vacía de 32 bits con añadir ruido para obtener una imagen que no contenga nada más que ruido.
Añadir y promediar imágenes ruidosas#
Al principio de este capítulo, indiqué cómo calcular la nueva desviación estándar del ruido cuando se suman dos píxeles ruidosos:
Eleva al cuadrado la desviación típica del ruido original para obtener la varianza de cada píxel
Añadir las desviaciones
Sacar la raíz cuadrada del resultado
Supongamos que tenemos dos imágenes (independientes) con la misma desviación típica del ruido Gaussiano, digamos 5. Aplicando este cálculo, si sumamos las imágenes, la desviación típica del ruido de la imagen resultante es
La desviación estándar del ruido de la imagen resultante es mayor.
Podríamos esperar que la suma de dos imágenes ruidosas sea, por tanto, peor: hemos aumentado el ruido. Sin embargo, debemos recordar que la señal también es mayor: de hecho, se ha duplicado (porque hemos sumado dos imágenes similares).
Si queremos una imagen de output con una señal similar a la de los originales, debemos promediar los valores de los píxeles correspondientes en lugar de sumar. En este caso, promediar es lo mismo que sumar, salvo que dividimos por dos. Al hacer esto, la desviación estándar del ruido también se reduce a la mitad y pasa a ser aproximadamente 3,54, es decir, es más baja que en cualquiera de las dos imágenes originales.
Esto es importante, porque implica que si tuviéramos que promediar dos imágenes ruidosas independientes de la misma escena con SNR similares, obtendríamos un resultado que contiene menos ruido, es decir, una SNR más alta.
Pero no hay que fiarse sólo de mi palabra. Podemos comprobar que realmente funciona mediante una simulación. {numref} fig-fig_noise_sum lo demuestra, y tiene una implicación muy práctica: la reducción de ruido promediando imágenes crea una mejor separación de picos en el histograma. Esto significa que, por lo general, debería darnos una imagen más susceptible a umbralización (thresholding).
Show code cell content
"""
Splitting one image to form two.
"""
# Load image
im = load_image('happy_cell.tif').astype(np.float32)
# Create two independeny noisy images
rng = np.random.default_rng(200)
im_noisy1 = im + rng.normal(scale=20, size=im.shape)
im_noisy2 = im + rng.normal(scale=20, size=im.shape)
# Average the images
im_sum = (im_noisy1 + im_noisy2)
im_averaged = im_sum / 2.0
fig = create_figure(figsize=(8, 4))
# Show the images and histograms
show_image(im_noisy1, clip_percentile=0.5, title="(A) First noisy image", pos=241)
show_image(im_noisy2, clip_percentile=0.5, title="(B) Second noisy image", pos=242)
show_image(im_sum, clip_percentile=0.5, title="(C) Sum of (A) and (B)", pos=243)
show_image(im_averaged, clip_percentile=0.5, title="(D) Average (A) and (B)", pos=244)
show_histogram(im_noisy1, pos=245)
show_histogram(im_noisy2, ylabel=None, pos=246)
show_histogram(im_sum, ylabel=None, pos=247)
show_histogram(im_averaged, ylabel=None, pos=248)
plt.tight_layout()
glue_fig('fig_noise_sum', fig)
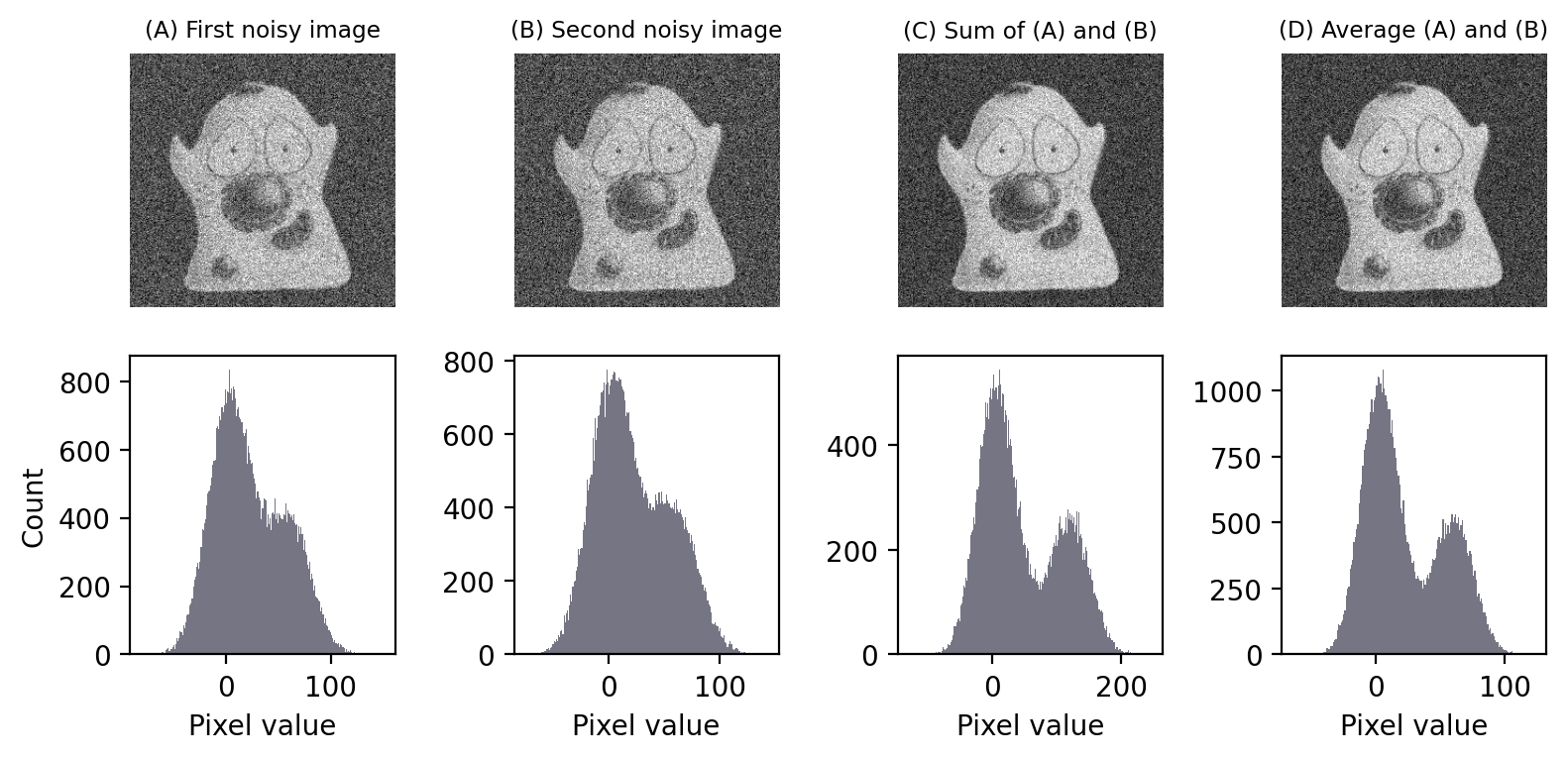
Figura 144 Suma y promedio de dos imágenes independientes con ruido Gaussiano. Tanto sumando como promediando se obtiene una imagen con una SNR mejorada, como puede verse en la mejor separación entre los picos del histograma.#
Añadir y promediar dentro de una imagen#
Todo esto significa que si se puede adquirir la misma imagen varias veces, al promediar las distintas imágenes se obtendría un resultado con menos ruido.
Por supuesto, no solemos tener varias imágenes independientes de todo lo que queramos analizar. En su lugar, sólo tenemos una imagen. Sin embargo, podemos explorar la idea dividiendo una sola imagen en dos, siempre que estemos dispuestos a sacrificar algo de resolución espacial.
Si tomamos los píxeles de cada dos columnas de la imagen, podemos extraerlos y combinarlos para formar otra imagen que parezca una versión comprimida de la original. Podemos hacer lo mismo con todas las columnas que nos hemos saltado, con lo que obtendremos dos imágenes reducidas, una de las columnas pares y otra de las impares.
Puedes ver en la figura Figura 145 que nuestras imágenes aplastadas parecen casi idénticas, porque los píxeles adyacentes suelen tener valores muy similares, fuera de las diferencias causadas por el ruido. Si promediamos estas imágenes, estas diferencias se compensan y obtenemos otra imagen de aspecto similar, pero con menos ruido.
Show code cell content
"""
Splitting one image to form two.
"""
# Load image
im = load_image('happy_cell.tif').astype(np.float32)
# Add noise
rng = np.random.default_rng(200)
im_noisy = im + rng.normal(size=im.shape) * 20
# Split left and right images
im_left = im_noisy[:, ::2]
im_right = im_noisy[:, 1::2]
# Average the images
im_averaged = (im_left + im_right) / 2.0
# fig = create_figure(figsize=(8, 3))
fig, axs = plt.subplots(nrows=2, ncols=4, dpi=200,
gridspec_kw={'height_ratios':[1.5,1]},
sharey='row',
figsize=(8, 3.5))
# Pad images for display
show_image(im_noisy, title="(A) Original image", axes=axs[0][0])
show_image(im_left, title="(B) Odd columns", axes=axs[0][1])
show_image(im_right, title="(C) Even columns", axes=axs[0][2])
show_image(im_averaged, title="(D) Average of odd & even columns", axes=axs[0][3])
show_histogram(im_noisy, axes=axs[1][0])
show_histogram(im_left, ylabel=None, axes=axs[1][1])
show_histogram(im_right, ylabel=None, axes=axs[1][2])
show_histogram(im_averaged, ylabel=None, axes=axs[1][3])
plt.tight_layout()
glue_fig('fig_noise_split', fig)
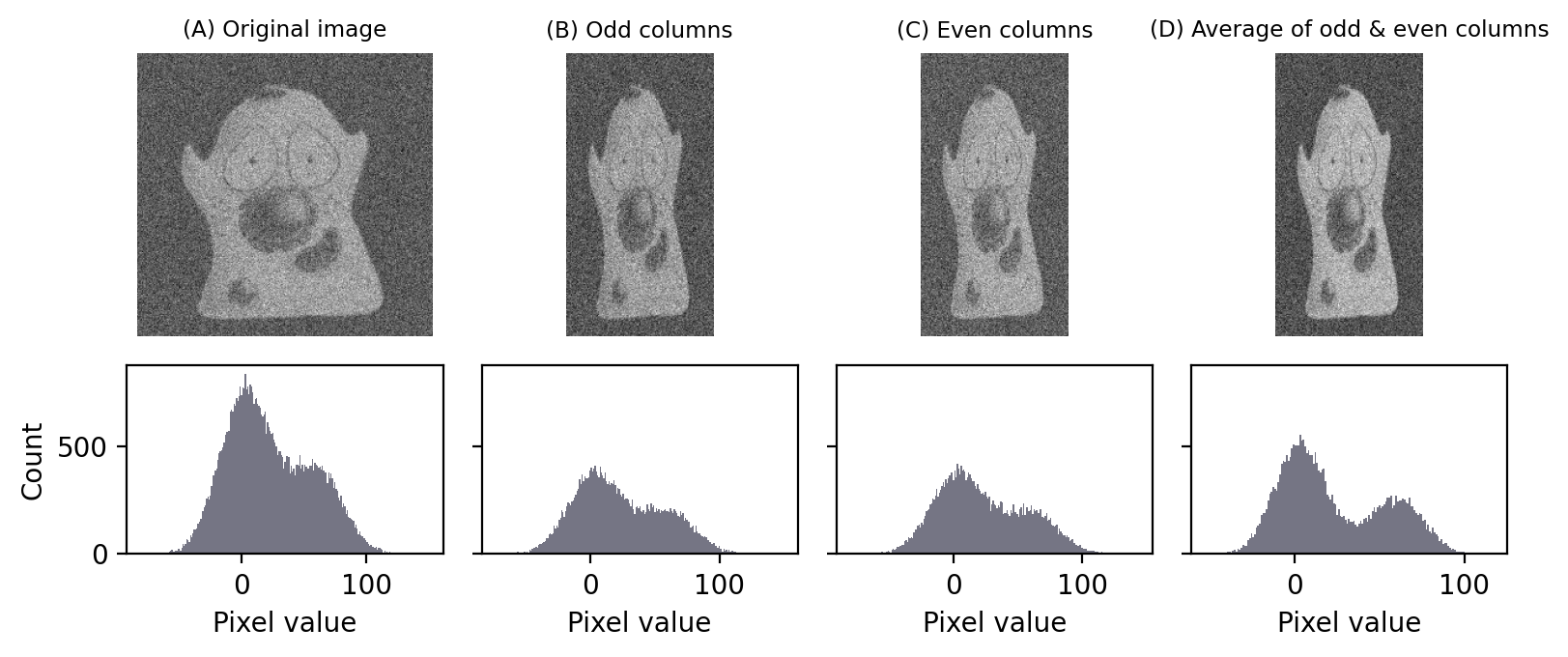
Figura 145 Crear dos imágenes a partir de una tomando columnas pares e impares. Si luego promediamos las dos imágenes, se reduce el ruido. La diferencia es sutil, pero se aprecia en la mejor separación de los picos en el histograma.#
Por supuesto, este truco tiene un inconveniente obvio: el aplastamiento es indeseable. Afortunadamente, podemos evitarlo simplemente promediando las columnas adyacentes pero sin dividirlas en imágenes separadas. Luego podemos hacer lo mismo con filas adyacentes. E incluso con las diagonales adyacentes, si lo deseamos.
Esta es precisamente la idea que subyace a nuestro uso de un 3×3 mean filter to reduce noise: no tenemos imágenes independientes para promediar, así que promediamos dentro de una imagen en su lugar (Figura 146).
Show code cell content
"""
Show the effect of averaging pixels.
"""
# Load image
im = load_image('happy_cell.tif').astype(np.float32)
# If we have fewer pixels, the differences will be easier to see
# im = im[::2, ::2]
# Add noise
rng = np.random.default_rng(200)
im_noisy = im + rng.normal(size=im.shape) * 20
# Compute the average of 2 adjacent pixels
kernel_2 = np.asarray([1, 1, 0]).reshape((1, 3)) / 2.0
im_noisy_2 = ndimage.convolve(im_noisy, kernel_2)
# Compute the average of 9 adjacent pixels
kernel_9 = np.ones((3, 3)) / 9.0
im_noisy_9 = ndimage.convolve(im_noisy, kernel_9)
# Compute same display settings to use for all images
im_args = dict(
vmin = np.percentile(im_noisy, 2),
vmax = np.percentile(im_noisy, 98)
)
# fig = create_figure(figsize=(8, 6))
fig, ax = plt.subplots(3, 3, sharey='row', dpi=200, figsize=(8, 8))
row = im.shape[0] // 2
line_args = ([0, im.shape[1]-1], [row, row], 'w--')
pos = 331
show_image(im_noisy, title='(A) Original image', **im_args, pos=pos)
plt.plot(*line_args)
pos += 1
show_image(im_noisy_2, title='(B) Averaging 2 adjacent pixels', **im_args, pos=pos)
plt.plot(*line_args)
pos += 1
show_image(im_noisy_9, title='(C) Averaging 9 adjacent pixels', **im_args, pos=pos)
plt.plot(*line_args)
pos += 1
show_plot(im_noisy[row, :], xlabel='x', ylabel='Value', linewidth=1, pos=pos)
pos += 1
show_plot(im_noisy_2[row, :], xlabel='x', linewidth=1, pos=pos)
pos += 1
show_plot(im_noisy_9[row, :], xlabel='x', linewidth=1, pos=pos)
pos += 1
show_histogram(im_noisy, pos=pos)
plt.xlim([-60, 120])
pos += 1
show_histogram(im_noisy_2, pos=pos)
plt.xlim([-60, 120])
pos += 1
show_histogram(im_noisy_9, pos=pos)
plt.xlim([-60, 120])
plt.tight_layout()
glue_fig('fig_filt_averaging', fig)
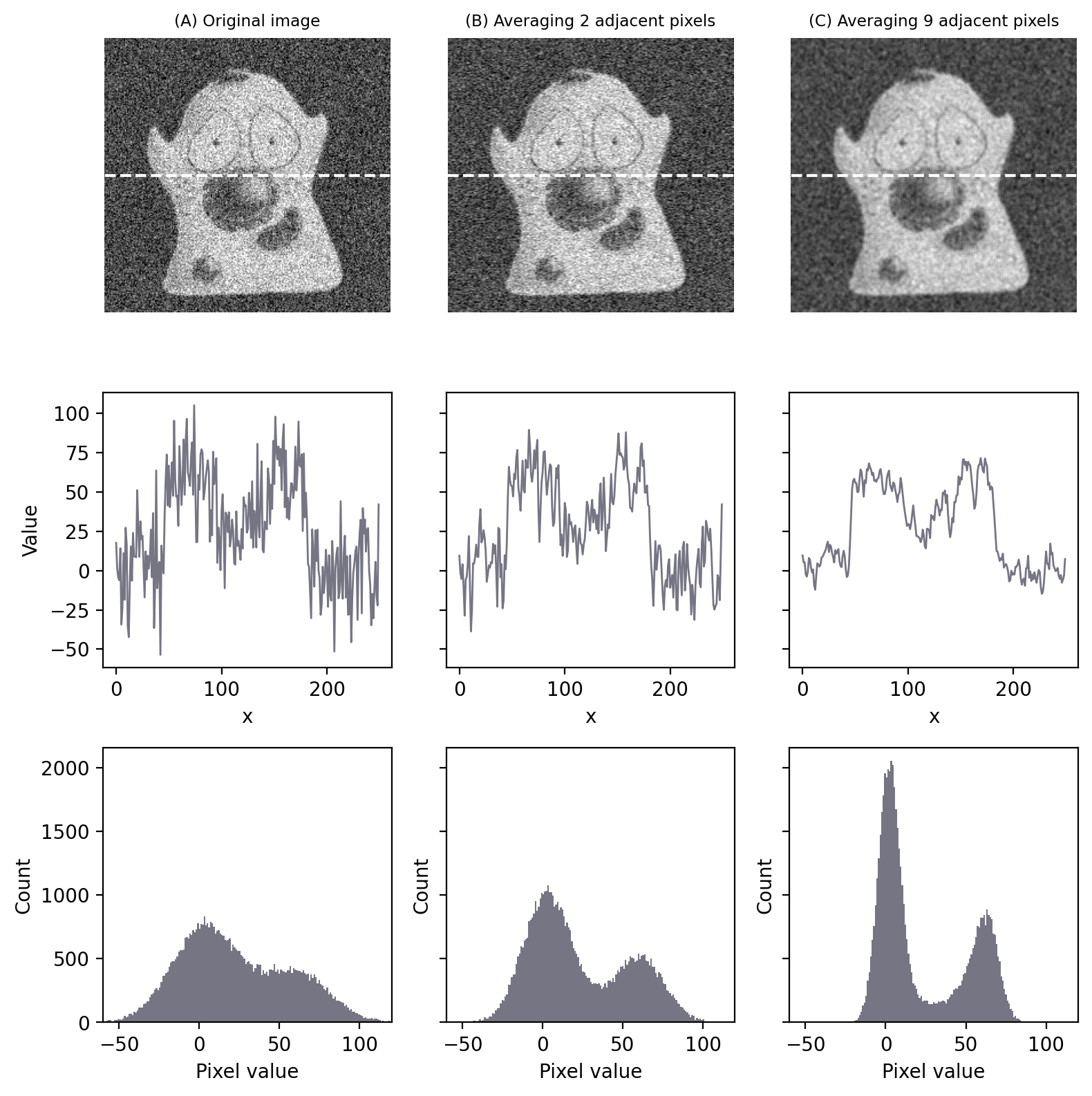
Figura 146 Reducción del ruido promediando píxeles adyacentes. Aunque el aspecto general de la imagen no ha cambiado mucho, los histogramas indican una separación mucho mayor entre el primer plano y el fondo, lo que significa que es más probable que los umbrales funcionen bien. En (C), el resultado es equivalente a aplicar un filtro de media 3×3.#
Esperamos que este análisis te ayude a comprender por qué los filtros son capaces de reducir el ruido Gaussiano. En la próxima sección, veremos cómo muchas de las mismas ideas se aplican también al ruido de Poisson.
Ruido de Poisson#
En 1898, Ladislaus Bortkiewicz publicó un libro titulado La ley de los números pequeños. Entre otras cosas, incluía un análisis, ahora famoso, del número de soldados de diferentes cuerpos de la caballería prusiana que morían al ser pateados por un caballo, medido a lo largo de un periodo de 20 años. En concreto, demostró que estas cifras siguen una distribución de Poisson.
Esta distribución, introducida por Siméon Denis Poisson en 1838, da la probabilidad de que un suceso ocurra un cierto número de veces, dado que conocemos (1) el ritmo medio al que ocurre y (2) que todos sus sucesos son independientes. Sin embargo, la utilidad de la distribución de Poisson va mucho más allá de los truculentos análisis militares y tiene aplicaciones muy diversas, como la probabilidad de emisión de fotones, que es intrínsecamente aleatoria.
Show code cell content
"""
Show Probability mass function for the Poisson distribution.
"""
fig = create_figure(figsize=(8, 4))
show_image('images/Poisson.jpg', title='Siméon Denis Poisson (1781–1840)', pos=121)
from scipy import stats
k = np.arange(20)
plt.subplot(122)
plot_params = dict(
color=None,
marker='o',
markersize=4,
title='Poisson distribution'
)
for mu in [1, 2, 5, 10]:
poisson = stats.poisson(mu)
show_plot(k, poisson.pmf(k), **plot_params, label=f'λ={mu}')
plt.legend()
plt.xlabel('k')
plt.tight_layout()
# show_image('images/maths_pmf_poisson.png', title='Poisson distribution', pos=122)
glue_fig('fig_noise_poisson', fig)
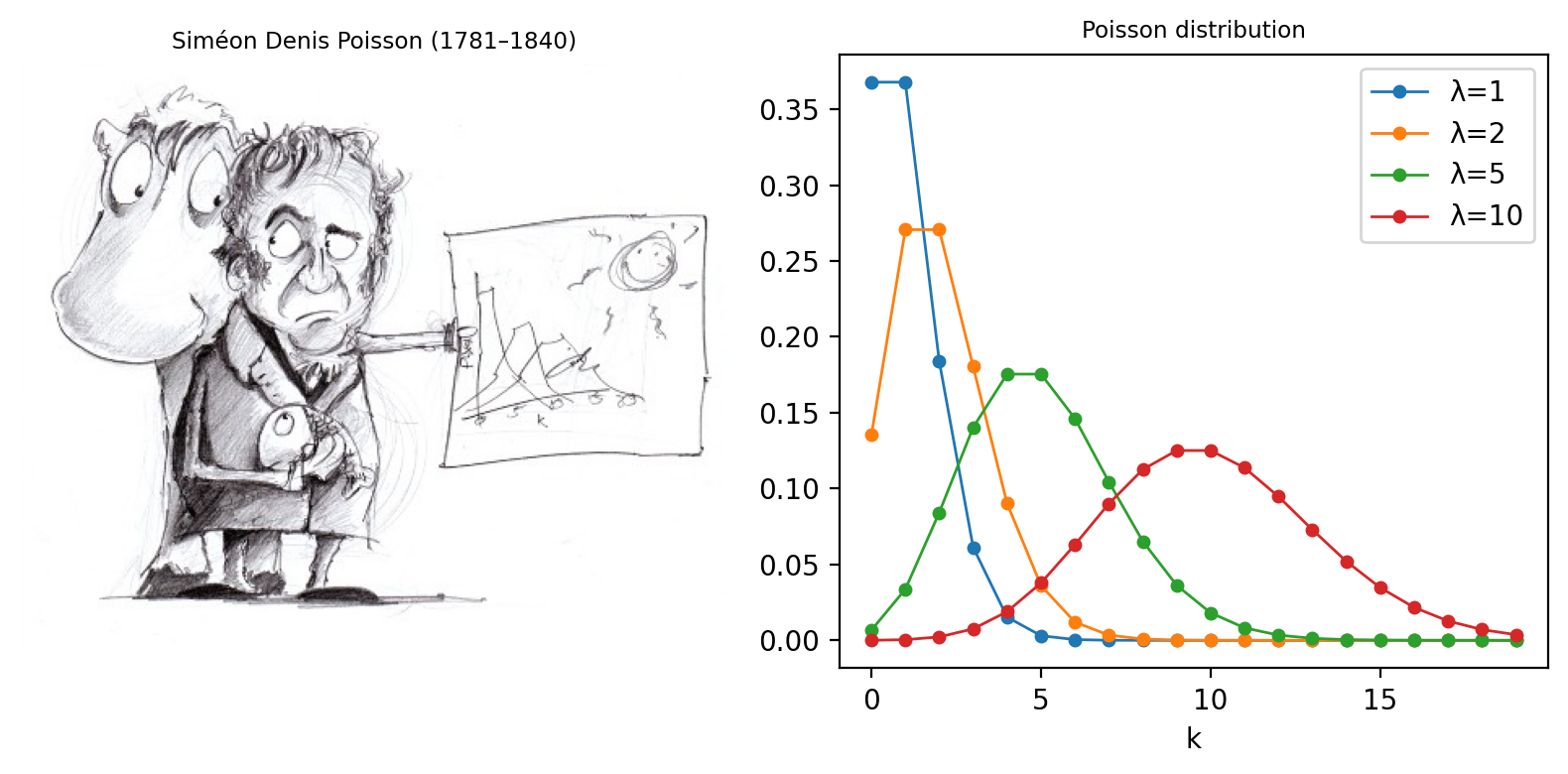
Figura 147 Siméon Denis Poisson y su distribución. (A) Se dice que Poisson era extremadamente torpe y descoordinado con las manos. Esto contribuyó a que abandonara su aprendizaje como cirujano y se dedicara a las matemáticas, donde el problema era menos debilitante, aunque aparentemente esto significaba que sus diagramas no solían estar muy bien dibujados (véase https://mathshistory.st-andrews.ac.uk/Biographies/Poisson/). (B) La «función de masa de probabilidad» de la distribución de Poisson para varios valores diferentes de λ. Esto permite ver, para cualquier «señal verdadera» λ, la probabilidad de contar realmente cualquier valor real k. Aunque es más probable que uno cuente exactamente k = λ que cualquier otro k posible, a medida que λ aumenta, la probabilidad de obtener precisamente este valor se hace cada vez más pequeña.#
Supongamos que, en promedio, se emitirá un solo fotón en alguna parte de una muestra fluorescente en un intervalo de tiempo determinado. La aleatoriedad implica que no podemos decir con seguridad qué ocurrirá en cada ocasión en que miremos; a veces se emitirá un fotón, a veces ninguno, a veces dos, a veces incluso más. Por lo tanto, lo que realmente nos interesa no es precisamente cuántos fotones se emiten, lo cual varía cada vez que miramos, sino la velocidad a la que se emitirían en condiciones fijas, que es una constante. La diferencia entre el número de fotones realmente emitidos y el verdadero ritmo de emisión es el ruido fotónico. El problema es que mantener las condiciones fijas puede no ser posible, lo que nos deja con el problema de intentar calcular las tasas a partir de mediciones únicas y ruidosas.
Ruido dependiente de la señal#
Evidentemente, puesto que es una tasa lo que queremos, podríamos obtenerla con más precisión si promediáramos muchas observaciones: al igual que con el ruido Gaussiano, promediar reduce el ruido de fotones. Por lo tanto, podemos esperar que los filtros de suavizado funcionen de forma similar para ambos tipos de ruido, y así es.
Sin embargo, la principal distinción entre los tipos de ruido es que el ruido de Poisson es dependiente de la señal, y cambia según el número de fotones emitidos (o detectados). Afortunadamente, la relación es sencilla: si la tasa de emisión de fotones es \(\lambda\), la varianza del ruido también es \(\lambda\), y la desviación típica del ruido es \(\sqrt{\lambda}\).
En realidad, esto no es tan inesperado como podría parecer a primera vista (véase Figura 148). Incluso puede observarse en una inspección muy cercana de Figura 149, en la que el aumento de la variabilidad en la neurona provoca su apariencia fantasmal incluso en una imagen que debería consistir (casi) exclusivamente en ruido.

Figura 148 La desviación estándar del ruido de los fotones es igual a la raíz cuadrada del valor esperado»__ Para entenderlo mejor, puede ser útil imaginar a un pescador que pesca muchas veces en el mismo lugar y en las mismas condiciones. Si pesca una media de 10 peces, sería razonable que pescara 7 ó 13 un mismo día, mientras que 20 sería excepcional. Si, por el contrario, pesca 100 peces de media, no sería excepcional que pescara 90 o 110 en un día concreto, aunque pescar sólo 10 sería extraño (y posiblemente decepcionante). Intuitivamente, el rango de valores que se considerarían probables está relacionado con el valor esperado. Aunque sólo sea por eso, esta analogía imperfecta puede ayudar al menos a recordar el nombre de la distribución que sigue el ruido de los fotones.#
Show code cell content
fig = create_figure(figsize=(8, 4))
r = 100
c = 100
s = 256
im = load_image('Rat_Hippocampal_Neuron.zip').astype(np.float32)[0, r:r+s, c:c+s]
im2 = ndimage.gaussian_filter(im, sigma=0.25)
im_diff = im - im2
show_image(im, clip_percentile=0.5, title='(A) Original image)', pos=131)
show_image(im2, clip_percentile=0.5, title='(B) Gaussian filtered image', pos=132)
show_image(im_diff, clip_percentile=5, title='(C) Result of (A) - (B)', pos=133)
glue_fig('fig_noise_neuron', fig)
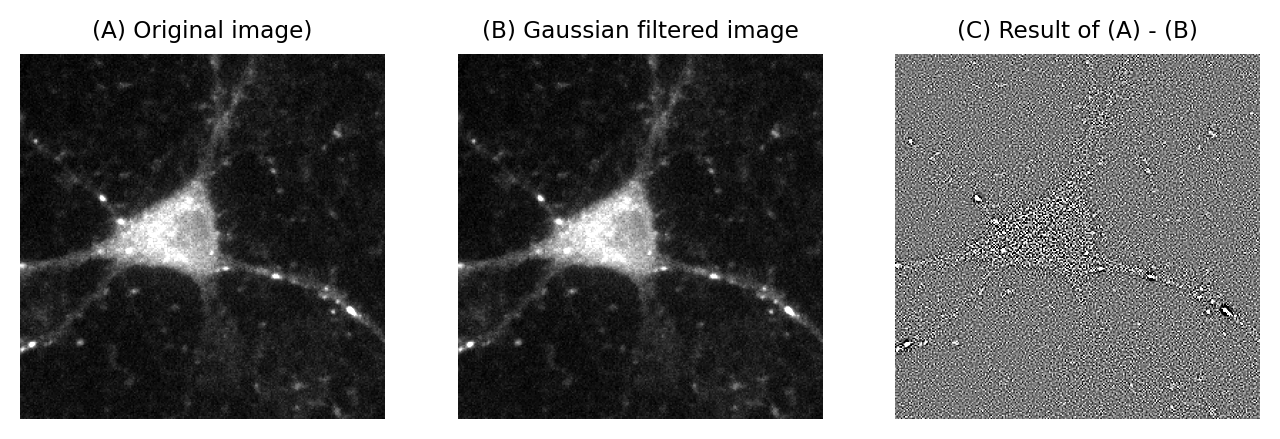
Figura 149 Demostración de que el ruido de Poisson cambia a lo largo de una imagen. (A) Parte de una imagen de microscopía de fluorescencia. (B) Una versión con filtro Gaussiano de (A) utilizando un filtro muy pequeño (\(\sigma\)=0,25). El filtrado Gaussiano reduce el ruido de una imagen sustituyendo cada píxel por una media ponderada de los píxeles vecinos (véase Filtros). (C) La diferencia entre la imagen original y la filtrada contiene el ruido que el filtrado ha eliminado. Las zonas más brillantes de la imagen original siguen siendo visibles en esta «imagen de ruido» como regiones de mayor variabilidad. Esto es en parte un efecto del ruido de Poisson que ha hecho que la desviación estándar del ruido sea mayor en las partes más brillantes de la imagen adquirida.#
La fórmula de la función de masa de probabilidad de la distribución de Poisson es:
donde
\(\lambda\) es la tasa media de ocurrencia del suceso (es decir, la tasa de emisión de fotones sin ruido que queremos)
\(k\) es un número real de ocurrencias para las que queremos calcular la probabilidad
\(k!\) es el factorial de \(k\) (es decir, \(k \veces (k-1) \veces (k-2) \veces ... \veces 1\))
Así, si se sabe que la tasa de emisión de fotones es 0.5, por ejemplo, se puede poner \(\lambda = 0.5\) en la ecuación y determinar la probabilidad de obtener cualquier valor particular (entero) de \(k\) fotones. Aplicando esto, la probabilidad de no detectar ningún fotón (\(k = 0\)) es 0.6065, mientras que la probabilidad de detectar un solo fotón (\(k = 1\)) es 0.3033$.
Lo que sabemos con certeza es que no es posible detectar 0.5 fotones: obtendremos un valor entero, no «parte de un fotón».
Suponiendo que la tasa media de emisión de fotones es 1, utiliza la ecuación (4) para calcular la probabilidad de detectar realmente 5 (que, con una tasa 5 veces superior a la verdadera, sería un resultado extremadamente inexacto). ¿Que tan común crees que es encontrar píxeles tan ruidosos en la región de fondo de una imagen oscura?
La probabilidad de detectar 5 fotones es de aproximadamente 0.0031.
Aunque se trata de una probabilidad muy baja, las imágenes contienen tantos píxeles que cabe esperar ver con frecuencia valores tan ruidosos. Por ejemplo, en una imagen bastante oscura y apagada de 512×512 píxeles en la que la tasa media de emisión de fotones es 1, cabría esperar que 800 píxeles tuvieran un valor de 5, y que dos píxeles incluso tuvieran un valor de 8. Por tanto, la presencia de píxeles brillantes u oscuros aislados suele decirnos muy poco, y sólo procesando la imagen con más cuidado y observando los valores circundantes podemos (a veces) descartar la posibilidad de que sean simplemente el resultado del ruido.
La SNR para el ruido de Poisson#
Si la desviación típica del ruido fuera lo único que importara, esto sugeriría que es mejor no detectar mucha luz: entonces la desviación típica del ruido fotónico es menor. Pero la SNR es una guía mucho más fiable. Para el ruido que sigue una distribución de Poisson, es especialmente fácil de calcular. Sustituyendo en la fórmula para la SNR (Equation (3)):
¡Por lo tanto la SNR del ruido fotónico es igual a la raíz cuadrada de la señal!
Esto significa que a medida que aumenta el número medio de fotones emitidos (y, por tanto, detectados), también lo hace la SNR. Más fotones → una mejor SNR, lo que conduce directamente a la afirmación
Importante
Si se quiere reducir el ruido fotónico, hay que detectar más fotones
Podemos visualizarlo mediante una simulación que muestra cómo una imagen y su histograma cambian con el tiempo a medida que se detectan más fotones.
Esto es lo mismo que decir que el promedio reduce el ruido. El promedio y la suma tienen el mismo efecto y sólo se diferencian por un factor de escala constante.
Por qué es importante la relatividad: un ejemplo sencillo
La SNR aumenta con el número de fotones, aunque la desviación estándar del ruido también aumente, porque lo que realmente nos interesa son las diferencias relativas en el brillo de algunas partes de la imagen. Los números absolutos suelen tener muy poca importancia, lo cual es una suerte, ya que no se detectan todos los fotones.
Sin embargo, si sigues sin estar convencido de que la desviación típica del ruido puede aumentar mientras mejora la situación, el siguiente ejemplo concreto podría ayudarte. Supongamos que la señal verdadera de un píxel es de 4 fotones. Suponiendo que el valor medido real esté dentro de una desviación estándar de ruido del resultado correcto (lo que será, aproximadamente, el 68% de las veces), se espera que esté en el rango 2-6. La señal real en otro píxel es el doble de fuerte – 8 fotones – y, por el mismo argumento, se espera medir un valor en el rango 5-11. Con recuentos de fotones tan bajos, aunque un píxel tenga el doble de valor que otro, a menudo no podemos discernir con seguridad que el valor verdadero, sin ruido, de ambos píxeles sea diferente.
Por otro lado, supongamos que la señal real del primer píxel es de 100 fotones, por lo que medimos algo en el rango de 90-110. El segundo píxel, todavía el doble de brillante, da una medida en el rango 186-214. Estos rangos son mayores, pero lo más importante es que ni siquiera se superponen, por lo que es muy fácil distinguir los píxeles. Por lo tanto, la desviación estándar del ruido por sí sola no es una buena medida de lo ruidosa que es una imagen. La SNR es mucho más informativa: la regla simple es que cuanto más alta, mejor. O, si aún así no te parece correcto, puedes darle la vuelta y considerar la relación ruido/señal (el ruido relativo), en cuyo caso más bajo es mejor (Figura 150).
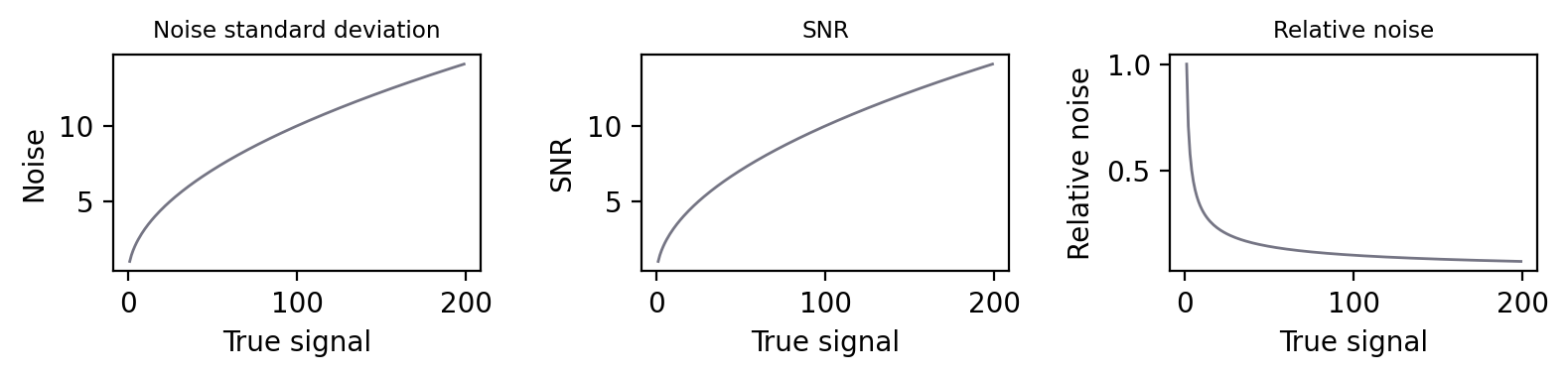
Figura 150 Para el ruido de Poisson, la desviación típica aumenta con la raíz cuadrada de la señal. Lo mismo ocurre con la SNR, por lo que los gráficos (A) y (B) son idénticos. Esta mejora de la SNR a pesar del aumento del ruido se debe a que la señal aumenta más rápido que el ruido, por lo que éste es relativamente menor. El ruido relativo (1/SNR) muestra este efecto (C).#
Ruido de Poisson y detección#
Entonces, ¿por qué debería importarte que el ruido de los fotones dependa de la señal?
Una de las razones es que puede facilitar o dificultar la detección de características de tamaños y brillos idénticos en una imagen debido únicamente al fondo local. Esto se ilustra en Figura 151.
Show code cell content
fig, axs = plt.subplots(figsize=(8, 6), dpi=200, sharex='col', sharey='row')
# Create a ramp image with increasing intensity
max_val = 200
width = 400
height = width // 5
spot_spacing = width // 10
spot_rel_intensity = 0.4
spot_abs_intensity = (max_val / 2) * spot_rel_intensity
x = np.linspace(0, max_val, width)
im_ramp = np.repeat(x.reshape((1, width)), height, axis=0)
# Create Gaussian spots, each with maximum intensity of 1
sigma = 2
row = height // 2
im_spots = np.zeros_like(im_ramp)
im_spots[row, spot_spacing::spot_spacing] = 1
im_spots = ndimage.gaussian_filter(im_spots, sigma)
im_spots = im_spots / im_spots.max()
# Add spots to ramp with same absolute or relative intensity
im_ramp_abs = im_ramp + im_spots * spot_abs_intensity
im_ramp_rel = im_ramp + im_ramp * im_spots * spot_rel_intensity
# Add poisson noise to each ramp
rng = np.random.default_rng(100)
im_ramp_abs_noise = rng.poisson(im_ramp_abs)
im_ramp_rel_noise = rng.poisson(im_ramp_rel)
plot_args = dict(
xlabel='Mean photons',
ylabel='Detected photons',
ylim=[0, im_ramp_rel_noise.max()],
xlim=None,
)
show_image(im_ramp_abs, title='Spots with the same absolute brightness', pos=421)
show_plot(x, im_ramp_abs[row,:], **plot_args, pos=423)
show_image(im_ramp_abs_noise, clip_percentile=0.5, pos=425)
show_plot(x, im_ramp_abs_noise[row,:], **plot_args, pos=427)
show_image(im_ramp_rel, title='Spots with the same relative brightness', pos=422)
show_plot(x, im_ramp_rel[row,:], **plot_args, pos=424)
show_image(im_ramp_rel_noise, clip_percentile=0.5, pos=426)
show_plot(x, im_ramp_rel_noise[row,:], **plot_args, pos=428)
plt.tight_layout()
glue_fig('fig_noise_poisson_ramp', fig)
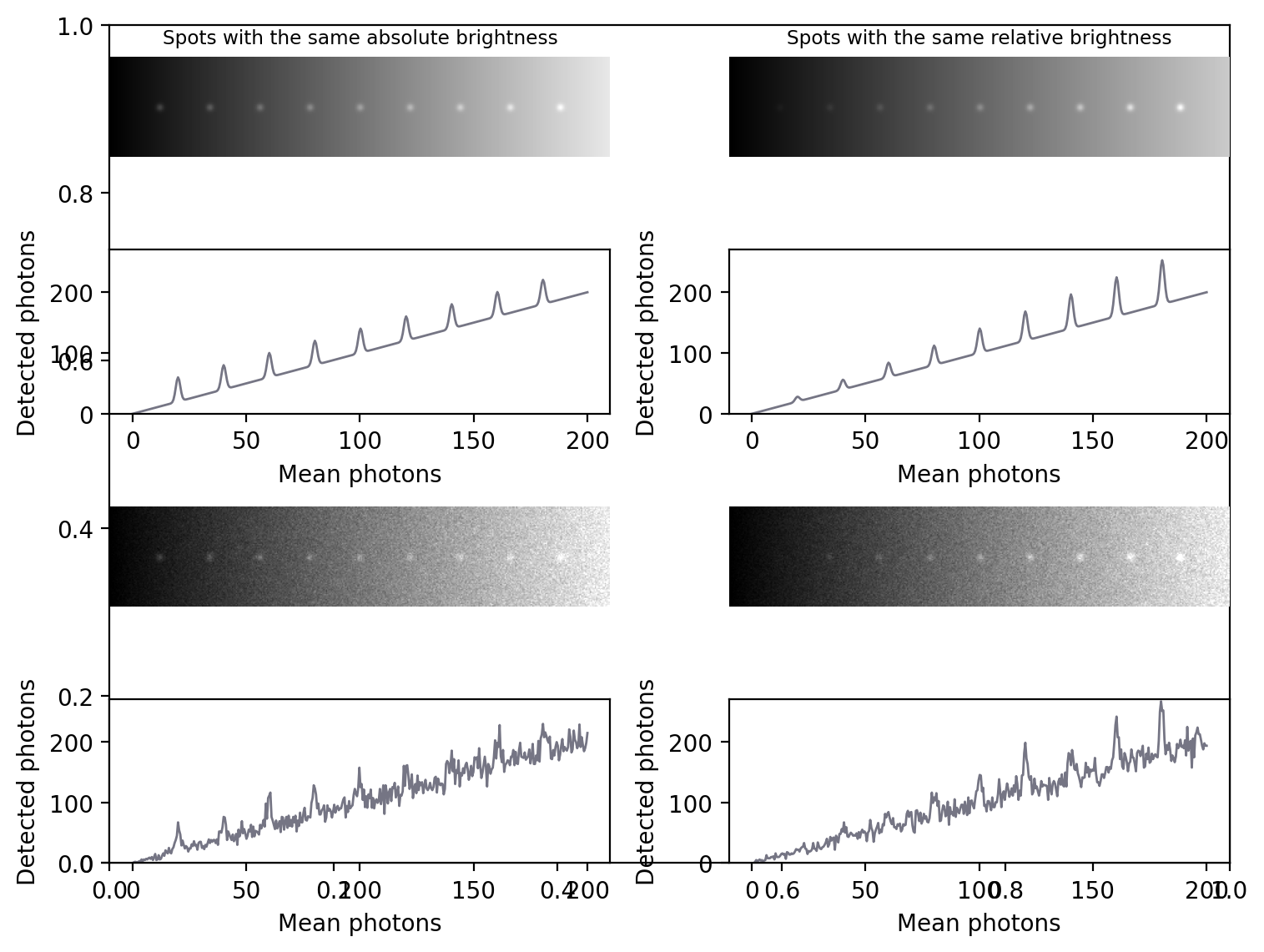
Figura 151 La dependencia de la señal del ruido de Poisson afecta al grado de visibilidad (y, por tanto, de detectabilidad) de las estructuras en una imagen. (A) Se añaden nueve manchas del mismo brillo absoluto a una imagen con un fondo que aumenta linealmente (arriba) y se añade ruido de Poisson (abajo). Como la variabilidad del ruido es mayor a medida que aumenta el fondo, las manchas de la parte más oscura de la imagen pueden verse claramente en el perfil, pero es más difícil distinguir las manchas de la parte más brillante. (B) Se añaden manchas del mismo brillo relativo al fondo, junto con ruido de Poisson. Como el ruido es ahora relativamente menor a medida que aumenta la luminosidad, sólo pueden verse las manchas de la parte más luminosa de la imagen, mientras que las de la parte más oscura quedan ocultas por el ruido.#
En general, si queremos ver un aumento de fluorescencia de un número fijo de fotones, es más fácil hacerlo si el fondo es muy oscuro. Pero si el aumento de fluorescencia se define relativo al fondo, será mucho más fácil identificarlo si el fondo es alto. En cualquier caso, cuando intentemos determinar el número de estructuras pequeñas en una imagen, por ejemplo, debemos recordar que el número que podremos detectar se verá afectado por el fondo cercano. Por lo tanto, los resultados obtenidos a partir de regiones claras y oscuras podrían no ser directamente comparables.
Abre las imágenes mystery_noise_1.tif y mystery_noise_2.tif en ImageJ.
Ambos tienen ruido, pero en uno el ruido sigue una distribución Gaussiana (como el ruido de lectura) y en el otro sigue una distribución de Poisson (como el ruido de fotones). ¿Cuál es cuál?
El ruido en mystery_noise_1.tif es Gaussiano; el ruido en mystery_noise_2.tif sigue una distribución de Poisson. Dado que hay regiones razonablemente planas dentro de la celula y el fondo, yo lo comprobaría dibujando una ROI dentro de cada una y midiendo las desviaciones estándar. Si son similares, el ruido es Gaussiano; si hay una gran diferencia, es probable que el ruido sea de Poisson.
Si no dispusiera de regiones planas, intentaría aplicar un filtro de gradiente con los coeficientes -1 1 0, e inspeccionar los resultados. Otra posibilidad sería trazar un perfil de fluorescencia o sustraer una versión ligeramente suavizada de cada imagen.
Combinación de fuentes de ruido#
Combinando nuestras fuentes de ruido, podemos imaginar un valor de píxel real como la suma de tres valores: la tasa real de emisión de fotones, el componente de ruido de fotones y el componente de ruido de lectura [^fn_5]. El primero de ellos es el que queremos, mientras que los dos últimos son números aleatorios que pueden ser positivos o negativos.
Show code cell content
fig, ax = plt.subplots(1, 4, figsize=(10, 2), dpi=200, sharey=True)
steps = np.power(2, np.arange(0, 9, 1))
steps = np.repeat(steps, 32, axis=0)
steps = np.concatenate([steps, steps[::-1]]).flatten()
rng = np.random.default_rng(100)
steps_poisson = rng.poisson(steps)
noise_gaussian = rng.normal(size=steps.shape) * 8
steps_gaussian = steps + noise_gaussian
steps_both = steps_poisson + noise_gaussian
ylim = [0, 320]
show_plot(steps, title='A noise-free signal', ylim=ylim, pos=141)
show_plot(steps_poisson, title='Photon noise', ylim=ylim, color=(0.4, 0, 0), pos=142)
show_plot(steps_gaussian, title='Read noise', ylim=ylim, color=(0, 0.4, 0), pos=143)
show_plot(steps_both, title='Photon + Read noise', ylim=ylim, color=(0, 0, 0.4), pos=144)
plt.tight_layout()
glue_fig('fig_noise_steps', fig)

Figura 152 Ilustración de la diferencia entre el ruido fotónico y el ruido de lectura. Cuando ambos se añaden a una señal (en este caso, una serie de pasos en los que el valor se duplica en cada paso superior), la importancia relativa de cada uno depende del valor de la señal. A niveles bajos de señal, esta duplicación es muy difícil de discernir en medio de cualquiera de los dos tipos de ruido, y más aún cuando están presentes ambos componentes de ruido.#
Esto se ilustra en Figura 152 utilizando una simple señal 1D consistente de una serie de pasos. Se le añaden valores aleatorios para simular el ruido de fotones y de lectura. Cuando la señal es muy baja (indicando pocos fotones), la variabilidad en el ruido de fotones es muy baja - ¡pero alta relativa a la señal (B)! Esta variabilidad aumenta cuando la señal aumenta. Sin embargo, en el caso del ruido de lectura (C), la variabilidad es similar en todas partes. Cuando ambos tipos de ruido se combinan en (D), el ruido de lectura domina completamente cuando hay pocos fotones, pero tiene muy poco impacto cuando la señal aumenta. El ruido de fotones ya ha dificultado la detección de diferencias relativas de brillo cuando hay pocos fotones; con el ruido de lectura, puede llegar a ser desesperante.
Por lo tanto, superar el ruido de lectura es fundamental para obtener imágenes con poca luz, y la elección del detector es extremadamente importante (véase Microscopios y detectores). Pero, siempre que sea posible, detectar más fotones es algo extremadamente bueno, ya que ayuda a superar ambos tipos de ruido.
Otras fuentes de ruido
Los fotones y el ruido de lectura son las principales fuentes de ruido que hay que tener en cuenta a la hora de diseñar y llevar a cabo un experimento. Otra fuente que se menciona a menudo en la bibliografía es el ruido oscuro, que se produce cuando un electrón caprichoso hace que el detector registre un fotón aunque en realidad no haya ninguno. En imágenes con muy poca luz, esto da lugar a píxeles brillantes espurios. Sin embargo, es menos probable que el ruido oscuro cause problemas si se detectan muchos fotones reales, y muchos detectores reducen su aparición enfriando el sensor.
Si el equipo funciona correctamente, es probable que no se puedan distinguir otras fuentes de ruido de estas tres. No obstante, los valientes que deseen saber más pueden encontrar una lista concisa y muy informativa de más de 40 fuentes de imprecisión en The 39 steps: a cautionary tale of quantitative 3-D fluorescence microscopy, de James Pawley (disponible en línea en diversas fuentes).
Supongamos que tienes una imagen que no contiene mucha luz, pero tiene algunos píxeles brillantes aislados.
¿Qué tipo de filtro podrías utilizar para eliminarlos? ¿Y es seguro suponer que se deben a ruido oscuro o algo similar, o puede que los píxeles correspondan a estructuras brillantes reales?
Un filtro de mediana es una opción popular para eliminar los píxeles brillantes aislados, aunque cuando se utiliza ImageJ a veces prefiero porque esto sólo pone la salida filtrada por la mediana en la imagen si el valor original era realmente extremo (de acuerdo con algún umbral definido por el usuario). Esto preserva la independencia del ruido en el resto de los píxeles – por lo que todavía se comporta de forma fiable y predecible como el ruido de Poisson + Gaussiano. Si es necesario, podemos reducir el ruido restante con un filtro Gaussiano.
Suponiendo que el tamaño de un píxel sea menor que la PSF (lo que suele ocurrir en microscopía), es una buena idea eliminar estos valores atípicos. No pueden ser estructuras reales, porque cualquier estructura real tendría que extenderse sobre una región al menos tan grande como la PSF. Sin embargo, si el tamaño del píxel es muy grande, es posible que no podamos descartar que los «valores atípicos» estén causados por estructuras brillantes reales.
Encontrar fotones#
Los fotones adicionales necesarios para superar el ruido pueden proceder de varias fuentes. Uno es simplemente adquirir imágenes más lentamente, dedicando más tiempo a detectar la luz. Si esto resulta demasiado duro para la muestra, puede ser posible grabar varias imágenes rápidamente. Si hay poco movimiento entre exposiciones, estas imágenes podrían sumarse o promediarse para obtener un efecto similar (Figura 153).
Show code cell content
"""
Show impact of adding images with Poisson noise.
"""
im = load_image('happy_cell.tif')
im = im / im.max()
# Create a stack of 1000 images with Poisson noise
rng = np.random.default_rng(200)
noisy_images = np.dstack([rng.poisson(im) for ii in range(1000)])
# Display in a similar way
im_args = dict(clip_percentile=1)
fig = create_figure(figsize=(8, 4))
show_image(noisy_images[:, :, 0], title='1 image', pos=141)
show_image(np.mean(noisy_images[:, :, :10], axis=2), title='10 images', **im_args, pos=142)
show_image(np.mean(noisy_images[:, :, :100], axis=2), title='100 images', **im_args, pos=143)
show_image(np.mean(noisy_images[:, :, :1000], axis=2), title='1000 images', **im_args, pos=144)
glue_fig('fig_noise_averaging', fig)
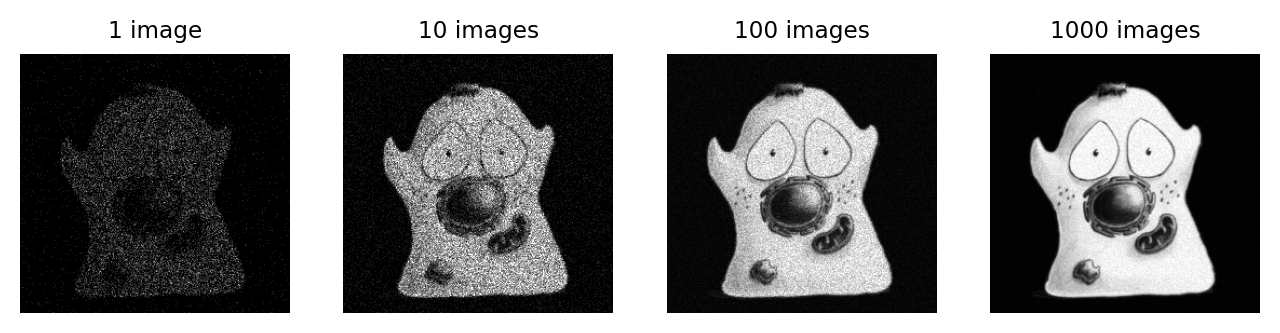
Figura 153 El efecto de añadir (o promediar) varias imágenes ruidosas, cada una independiente con una SNR similar.#
Una alternativa sería aumentar el tamaño del píxel, de forma que cada píxel incorpore fotones de regiones más grandes – aunque claramente esto tiene un coste en información espacial. Una forma de hacerlo es mediante binning.
Sin embargo, el ruido no puede eliminarse por completo durante la adquisición. Comprender su comportamiento, y sobre todo cómo filters puede reducirlo, puede ayudarnos a hacerle frente durante el análisis.
Show code cell content
fig = create_figure(figsize=(8, 4))
def bin2x2(im):
"""
Apply 2x2 binning to the pixels of a 2D image.
Note that if the dimensions are not even numbers then the final row/column
of pixels may have to be trimmed.
"""
r = int(np.floor(im.shape[0]/2)*2)
c = int(np.floor(im.shape[1]/2)*2)
return im[0:r:2, 0:c:2] + im[1:r:2, 0:c:2] + im[0:r:2, 1:c:2] + im[1:r:2, 1:c:2]
# Simulate larger bins by progressively applying 2x2 binning
im = load_image('images/nyquist_shannon.png')
assert im.shape == (512, 512)
im = im.astype(np.float32)
im2 = bin2x2(im)
im4 = bin2x2(im2)
im8 = bin2x2(im4)
im16 = bin2x2(im8)
show_image(im8, title='64 x 64 pixels', pos=131)
show_image(im4, title='128 x 128 pixels', pos=132)
show_image(im, title='512 x 512 pixels', pos=133)
glue_fig('fig_noise_nyquist_shannon', fig)
Muestreo Nyquist y elección del tamaño de píxel
Los píxeles pequeños son necesarios para ver los detalles, pero también reducen el número de fotones por píxel y, por tanto, aumentan el ruido. Sin embargo, Desenfoque y Función de dispersión de punto (Point Spread Function o PSF por sus siglas en inglés) ya ha argumentado que, en última instancia, no es el tamaño del píxel, sino la PSF lo que limita la resolución espacial – lo que sugiere que hay un tamaño mínimo de píxel por debajo del cual no se gana nada, y el único resultado es que se añade más ruido.
Este tamaño puede determinarse basándose en el conocimiento de la PSF y el teorema de muestreo Nyquist-Shannon (Figura 154). Se dice que las imágenes adquiridas con este tamaño de píxel están muestreadas por Nyquist (aunque véase la épica A Biography of the Pixel de Alvy Ray Smith para saber por qué el mérito del teorema de muestreo pertenece realmente a Vladimir Kotelnikov).
La forma más fácil que conozco de determinar el tamaño de píxel correspondiente para un experimento determinado es utilizar la calculadora en línea que ofrece Scientific Volume Imaging en https://svi.nl/NyquistCalculator. Es posible que necesites píxeles más grandes para reducir el ruido o ver un campo de visión más amplio, pero no obtendrás nada extra utilizando píxeles más pequeños.

Figura 154 Harry Nyquist (1889-1975) y Claude Shannon (1916-2001), muestrearon utilizando distintos tamaños de píxel. Su trabajo se utiliza para determinar los tamaños de píxel necesarios para maximizar la información disponible al adquirir imágenes, que depende del tamaño de la PSF.#

