Procesamiento multidimensional#
Outline del capítulo
Muchas operaciones de procesamiento se pueden ampliar más allá de 2 dimensiones
Agregar dimensiones adicionales puede aumentar en gran medida los requisitos computacionales
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Hasta ahora, en términos de procesamiento de imágenes nos hemos concentrado únicamente en imágenes 2D. La mayoría de las operaciones que hemos considerado también se pueden aplicar a datos 3D y, a veces, a datos con más dimensiones, en los casos en que esto sea significativo.
Esta breve descripción general del procesamiento multidimensional describe algunas de las cuestiones a considerar al extender el análisis más allá de dos dimensiones y ofrece algunas sugerencias sobre herramientas especializadas.
Nos centraremos en imágenes 3D: específicamente, en z-stacks.
¿Qué pasa con los canales y el tiempo?
Las 5 dimensiones principales que se encuentran comúnmente en el análisis de bioimágenes son x, y, z, canales y tiempo. Los tres primeros son similares (espaciales), mientras que los dos últimos son algo diferentes.
Aunque consideramos que los canales son otra dimensión [en capítulos anteriores] (chap_dimensions), generalmente no aplicamos operaciones (por ejemplo, filtros, umbrales) a través de canales o tiempo. Más bien, generalmente dividimos los canales o puntos de tiempo durante el procesamiento (por ejemplo, para detectar núcleos de un canal y un límite celular en un segundo canal) y luego combinamos las ROI o las mediciones al final.
Esto significa que los pasos clave de procesamiento no requieren una dimensión adicional de canales o tiempo.
En el caso del tiempo, el paso de «combinación» puede implicar vincular objetos para rastrearlos. Para esto se pueden utilizar herramientas como el fantástico Trackmate.
análisis de imágenes nD
Si una técnica funciona para imágenes nD, esto indica que puede manejar cualquier cantidad de dimensiones. El paquete SciPy [Procesamiento de imágenes multidimensionales] (https://docs.scipy.org/doc/scipy/reference/ndimage.html) adopta esto y se importa como scipy.ndimage.
Segmentación en 3D#
La segmentación de imágenes generalmente implica generar imágenes binarias y anotadas.
La mayoría de las operaciones de procesamiento que hemos analizado para ayudar a realizar la segmentación de imágenes se extienden naturalmente al 3D (y más allá), aunque existen algunas consideraciones adicionales.
Umbral#
Los umbrales normalmente se determinan mediante el histograma de la imagen. Esto se calcula a partir de todos los píxeles de la imagen; el número de dimensiones realmente no importa.
La consideración principal para el establecimiento de umbrales en 3D es si los otros cortes z podrían introducir algún tipo de sesgo furtivo. Una ocasión en la que esto podría suceder es si las imágenes se adquieren con diferentes números de cortes, p.ej. algunos contienen más planos desenfocados que otros (Figura 129). Estos planos adicionales podrían afectar el histograma y las estadísticas de la imagen y, por lo tanto, cualquier umbral automatizado. Una imagen con muchas secciones desenfocadas puede tener un umbral diferente al de una imagen con pocos sectores.
Una solución para esto puede ser extraer un número fijo de cortes de cada imagen, por ejemplo, 10 cortes centrados en el volumen de interés dentro de la imagen. En general, esto debería hacer que las imágenes sean más comparables.
Show code cell content
im = np.zeros((64, 128, 128))
im[32, 64, 64] = 1.0
im = ndimage.gaussian_filter(im, sigma=(3, 32, 32))
im = np.expand_dims(im, axis=-1)
im = (im > im.max()/2).astype(np.float32) * 6
im = im + np.random.default_rng(100).normal(size=im.shape)
# Convert to float32 and rescale per channel (to simplify display later)
im = im.astype(np.float32)
for c in range(im.shape[-1]):
im[..., c] = im[..., c] - np.percentile(im[..., ], 0.25)
im[..., c] = im[..., c] / np.percentile(im[..., ], 99.75)
def show_orthogonal(im, axes, loc=None, projection=None, colors=None, show_slices=False, title=None):
"""
Show orthogonal slices or projections.
"""
from mpl_toolkits.axes_grid1 import make_axes_locatable
n_channels = im.shape[-1] if im.ndim > 3 else 1
if colors is None:
if n_channels == 1:
colors = ('white',)
elif n_channels == 2:
colors = ('green', 'magenta')
elif n_channels == 3:
colors = ('red', 'green', 'blue')
else:
raise ValueException('Colors must be specified if the number of channels is > 3!')
if axes is None:
fig = create_figure()
ax = fig.gca()
else:
ax = axes
if loc is None and projection is None:
loc = tuple(s//2 for s in im.shape)
# Create axes for orthogonal views
divider = make_axes_locatable(ax)
ax_xz = divider.append_axes("bottom", size="50%", pad=0.1, sharex=ax)
ax_yz = divider.append_axes("left", size="50%", pad=0.1, sharey=ax)
# Generate slices or projections
if projection:
imxy = projection(im, axis=0)
imxz = projection(im, axis=2)
imyz = np.moveaxis(projection(im, axis=1), 0, 1)
else:
imxy = im[loc[0],...]
imxz = im[:, loc[1],...]
imyz = np.moveaxis(im[:, :, loc[2],:], 0, 1)
show_image(create_rgb(imyz, colors),
axes=ax_yz, vmin=0, vmax=1)
if show_slices:
ax_yz.plot([loc[0], loc[0]], [0, im.shape[2]-1], 'w--', linewidth=1)
ax_yz.set_xlabel('z')
ax_yz.set_xticks([])
ax_yz.set_ylabel('y', rotation=0, va='center', ha='right')
ax_yz.set_yticks([])
ax_yz.set_axis_on()
show_image(create_rgb(imxy, colors),
axes=ax,
vmin=0, vmax=1)
if show_slices:
row = loc[1]
col = loc[2]
ax.plot([0, im.shape[1]-1], [row, row], 'w--', linewidth=1)
ax.plot([col, col], [0, im.shape[2]-1], 'w--', linewidth=1)
show_image(create_rgb(imxz, colors),
axes=ax_xz,
vmin=0, vmax=1)
if show_slices:
ax_xz.plot([0, im.shape[1]-1], [loc[0], loc[0]], 'w--', linewidth=1)
ax_xz.set_xlabel('x')
ax_xz.set_xticks([])
ax_xz.set_ylabel('z', rotation=0, va='center', ha='right')
ax_xz.set_yticks([])
ax_xz.set_axis_on()
plt.tight_layout()
if title:
ax.set_title(title)
im = np.expand_dims(im, axis=-1)
im = im[..., 0]
im_tight = im[24:-24, ...]
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
from skimage.filters import threshold_triangle, threshold_otsu
show_orthogonal(im_tight, show_slices=True, axes=axes[0, 0])
show_orthogonal(im_tight > threshold_otsu(im_tight), show_slices=True, axes=axes[0, 1])
show_histogram(im_tight, bins=256, axes=axes[0, 2])
show_orthogonal(im, show_slices=True, axes=axes[1, 0])
show_orthogonal(im > threshold_otsu(im), show_slices=True, axes=axes[1, 1])
show_histogram(im, bins=256, axes=axes[1, 2])
glue_fig('fig_multi_thresholds', fig)
## Create another figure for the question below
bw_tight_triangle = im_tight > threshold_triangle(im_tight)
bw_triangle = im > threshold_triangle(im)
fig, axes = plt.subplots(1, 2, figsize=(12, 8))
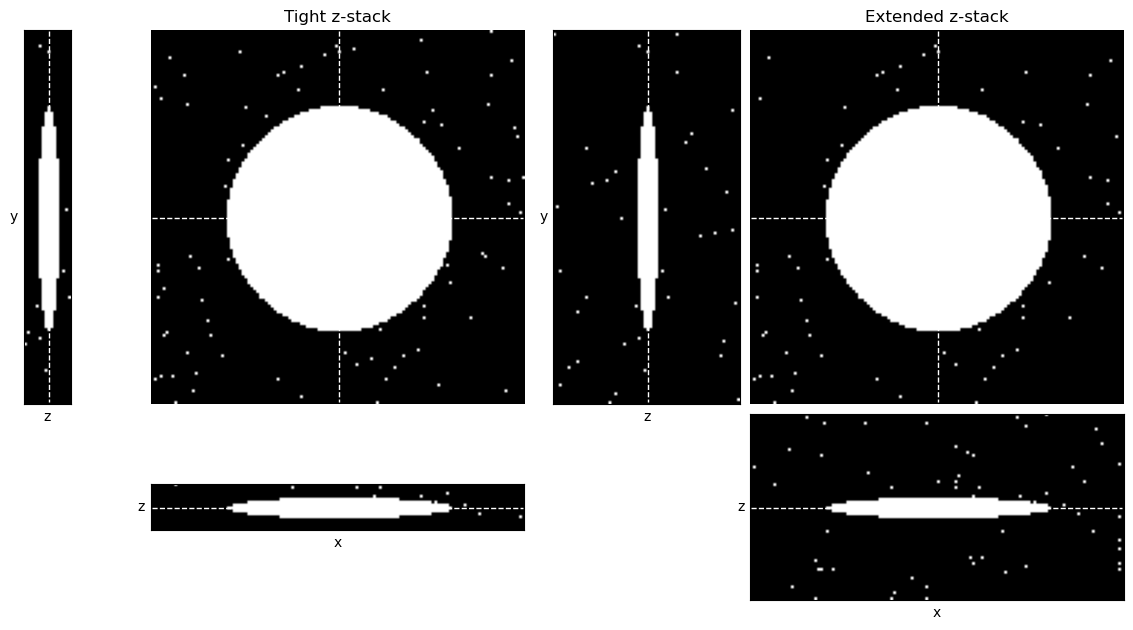
show_orthogonal(bw_tight_triangle, title='Tight z-stack', show_slices=True, axes=axes[0])
show_orthogonal(bw_triangle, title='Extended z-stack', show_slices=True, axes=axes[1])
glue_fig('fig_multi_thresholds_triangle', fig)
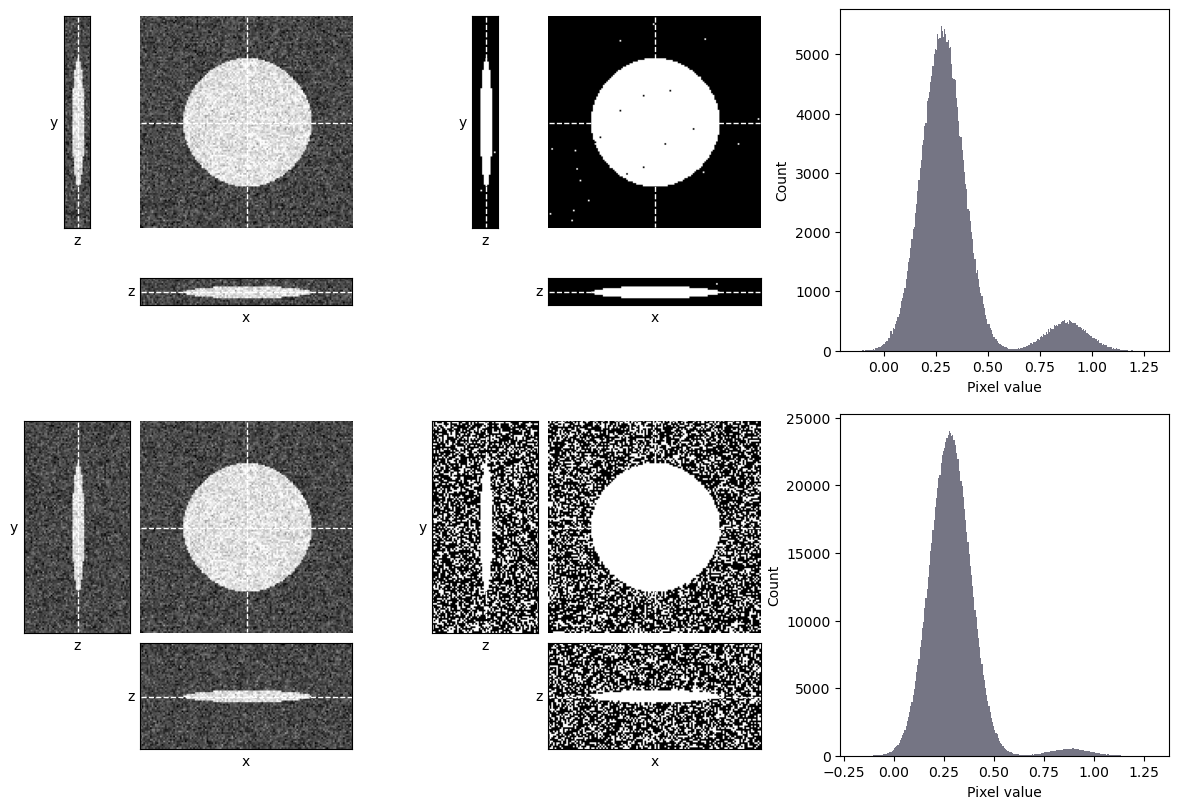
Figura 129 El umbral de una pila z puede verse influenciado por el número de cortes desenfocados. Aquí, se aplica un umbral automatizado determinado utilizando el [método de Otsu] (sec_thresholds_otsu) a dos pilas z que muestran el mismo objeto. La pila superior contiene algunos sectores desenfocados, mientras que la pila inferior contiene exactamente los mismos datos, y sectores adicionales que solo contienen ruido. El método de Otsu se adapta bien a la pila superior y funciona bien; sin embargo, falla gravemente en la pila inferior, donde hay una proporción mucho mayor de píxeles de fondo, por lo que el pico de fondo es más dominante.#
¿Cómo esperarías que Figura 129 difiera si se usara el método del triángulo para determinar el umbral, en lugar del método de Otsu?
En este caso, el método del triángulo funciona bien. En ambos casos, establece el umbral apropiadamente al pie del pico de fondo.
Filtros#
Los filtros lineales se pueden extender fácilmente a nD definiendo un núcleo de filtro con el número deseado de dimensiones. Sin embargo, esto puede aumentar drásticamente los requisitos computacionales, por lo que debemos comenzar a considerar el rendimiento.
Por ejemplo, supongamos que tenemos un filtro de 3×3. Siguiendo el algoritmo de filtrado lineal [descrito anteriormente] (sec_filters_linear), tendríamos que realizar 9 multiplicaciones y sumas para determinar el valor de cada píxel en la imagen de salida. Si nuestra imagen tiene un tamaño de 1000×1000 píxeles, eso sugiere 9.000.000 de multiplicaciones y sumas. Esto parece mucho, pero las computadoras modernas son rápidas, por lo que es poco probable que lo notemos.
Sin embargo, si tenemos un filtro de 3×3×3, entonces cada píxel de salida depende de 27 píxeles de entrada. Y los cortes adicionales significan que es probable que nuestra imagen sea más grande; digamos, 1000×1000×10 píxeles. Ahora tenemos que realizar cálculos con 270.000.000 píxeles, es decir, muchos más. Aún así, incluso eso probablemente sea rápido hoy en día.
¿Pero hasta qué punto podemos llegar? Un filtro de 11×11 implica 121 píxeles. Pero un filtro de 11×11×11 implica 1331. Para filtros e imágenes más grandes, podemos aumentar rápidamente los cálculos involucrados hasta que el procesamiento sea muy lento.
La situación mejora dramáticamente si un filtro es separable. Esto significa que en lugar de aplicar, por ejemplo, un único filtro de 11×11×11 (1331 coeficientes), podemos aplicar tres filtros separados de 11×1 orientados a lo largo de cada dimensión (33 coeficientes).
No todos los filtros lineales son separables, pero muchos de los más comunes sí lo son. Esto incluye filtros medios (según la forma del vecindario) y filtros Gaussianos. El resultado de aplicar el filtro por separado debe ser el mismo que el resultado de aplicar un filtro multidimensional denso (Figura 130). Pueden surgir algunas pequeñas diferencias a través del manejo de [redondeo y profundidades de bits] (chap_bit_depths), pero es casi seguro que la mejora en el rendimiento vale la pena por cualquier pequeño error introducido al aplicar un filtro por separado.
Show code cell content
"""
Demonstrate how Gaussian filters may be separable.
"""
fig = create_figure(figsize=(8, 5))
import numpy as np
from scipy import ndimage
im = load_image('happy_cell.tif').astype(np.float32)
sigma = 8
show_image(im, title="(A) Original image", pos=231)
# Filter horizontally, then vertically
im_h = ndimage.gaussian_filter1d(im, sigma, axis=1)
show_image(im_h, title="(B) Horizontally smoothed (A)", pos=232)
# Filter vertically, then horizontally
im_v = ndimage.gaussian_filter1d(im, sigma, axis=0)
show_image(im_v, title="(C) Vertically smoothed (A)", pos=233)
# Admission... the docs for gaussian_filter state that it's implemented separably -
# so this doesn't really demonstrate that 2D filtering is the same
# (except inasmuch as ndimage treats them equivalently)
im_gauss = ndimage.gaussian_filter(im, sigma)
show_image(im_gauss, title="(D) 2D Gaussian filtered (A)", pos=234)
im_hv = ndimage.gaussian_filter1d(im_h, sigma, axis=0)
show_image(im_hv, title="(E) Vertically smoothed (B)", pos=235)
im_vh = ndimage.gaussian_filter1d(im_v, sigma, axis=1)
show_image(im_vh, title="(F) Horizontally smoothed (C)", pos=236)
plt.tight_layout()
glue_fig('fig_gauss_separable', fig)
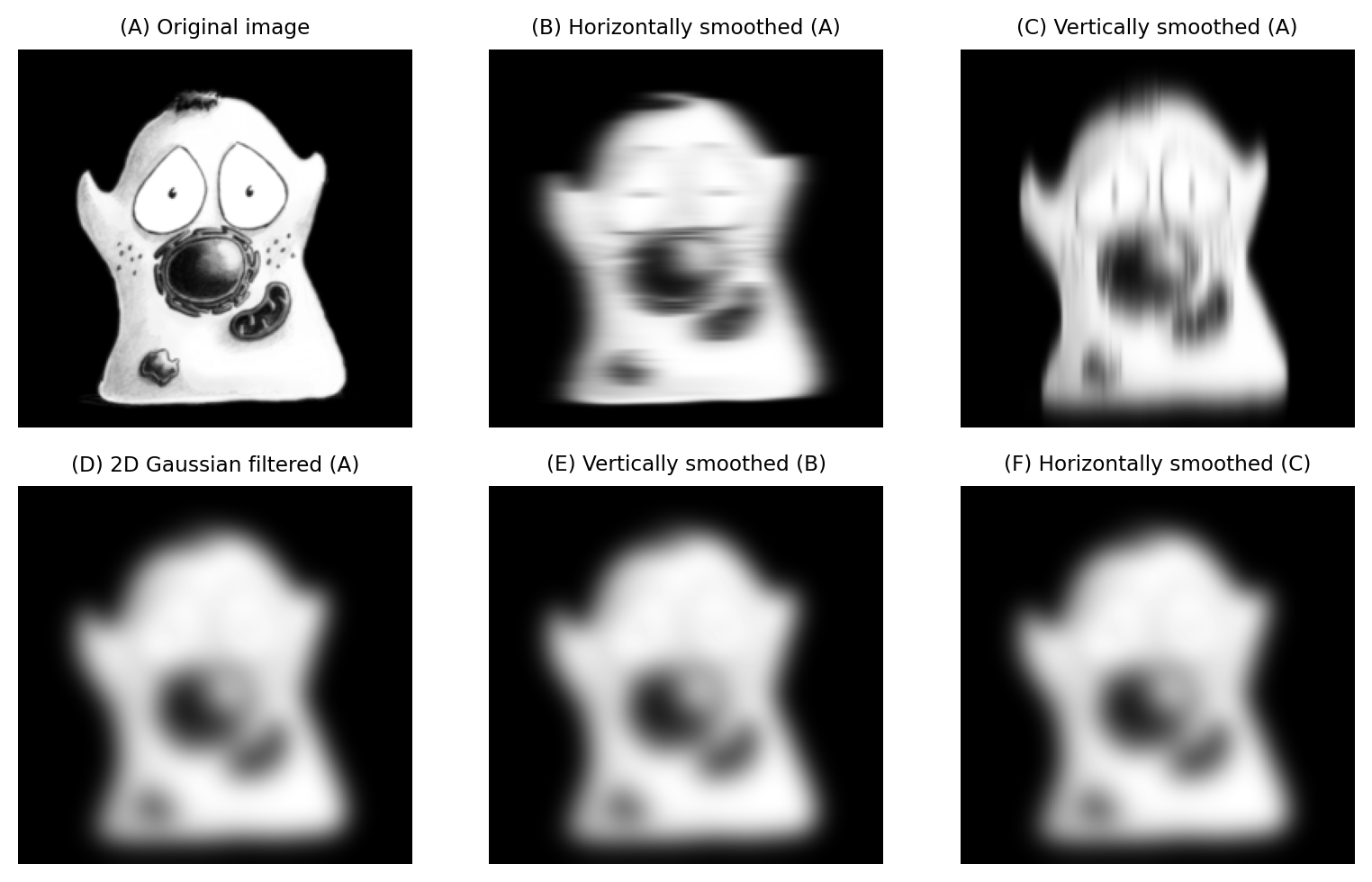
Figura 130 El suavizado Gaussiano 2D se puede aplicar usando un único filtro 2D o filtrando secuencialmente filas o columnas de la imagen: el resultado final es el mismo (hasta el error de redondeo). El orden del filtrado separable no importa.#
Las consideraciones son similares para los filtros no lineales: cuando agregamos más dimensiones, el tamaño de la vecindad puede aumentar rápidamente y ralentizar los cálculos. La separabilidad puede ayudar con algunos filtros no lineales (por ejemplo, mínimo y máximo, según la forma de la ventana), pero no con todos. Los filtros de mediana en particular son difíciles de optimizar y pueden ser extremadamente lentos cuando la vecindad es grande y/o más de 2D.
Isotropía y anisotropía.
Como se explicó en Tamaño y dimensiones de píxeles, el ancho y el alto de los píxeles suelen ser los mismos. Para una pila z, el espaciado z podría ser igual que el ancho y el alto, en cuyo caso los píxeles se denominan isotrópicos. Pero muy a menudo el espaciado z es diferente, lo que significa que los píxeles son anisotrópicos.
Es útil tener esto en cuenta al elegir los tamaños de filtro. Por ejemplo, normalmente establecería el valor \(\sigma\) para un filtro Gaussiano 3D según el tamaño del píxel.
Supongamos que el ancho y el alto del píxel son ambos de 0.5 µm y que el espaciado z es de 1 µm. Entonces podría elegir \(\sigma_x\) = 2 px, \(\sigma_y\) = 2 px y \(\sigma_z\) = 1 px para compensar la diferencia.
Ten en cuenta que algunos programas pueden permitirte ingresar \(\sigma\) en µm directamente y realizar la conversión a píxeles automáticamente.
Show code cell content
"""
Demonstrate how minimum filters may be separable.
"""
fig = create_figure(figsize=(8, 5))
import numpy as np
from scipy import ndimage
im = load_image('fixed_cells.png')
# im = load_image('happy_cell.tif')
size = 15
show_image(im, title="(A) Original image", pos=231)
# Filter horizontally, then vertically
im_h = ndimage.minimum_filter1d(im, size, axis=1)
show_image(im_h, title="(B) Horizontally filtered (A)", pos=232)
# Filter vertically, then horizontally
im_v = ndimage.minimum_filter1d(im, size, axis=0)
show_image(im_v, title="(C) Vertically filtered (A)", pos=233)
im_gauss = ndimage.minimum_filter(im, (size, size))
show_image(im_gauss, title="(D) 2D Minimum filtered (A)", pos=234)
im_hv = ndimage.minimum_filter1d(im_h, size, axis=0)
show_image(im_hv, title="(E) Vertically filtered (B)", pos=235)
im_vh = ndimage.minimum_filter1d(im_v, size, axis=1)
show_image(im_vh, title="(F) Horizontally filtered (C)", pos=236)
plt.tight_layout()
glue_fig('fig_multi_min_separable', fig)
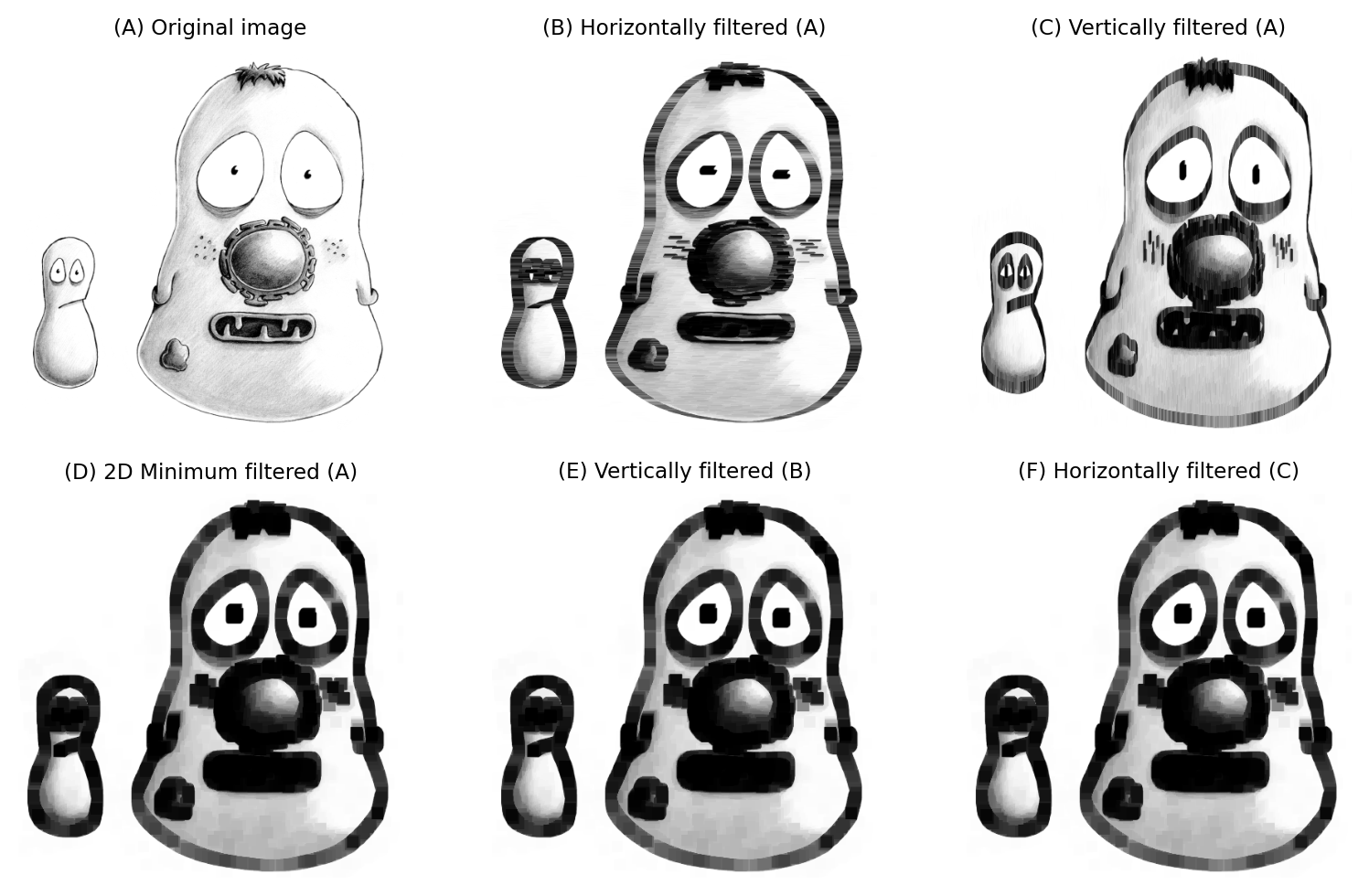
Figura 131 Un filtro mínimo de 15×15 aplicado de forma separable.#
Operaciones morfológicas#
La erosión, la dilatación, la apertura y el cierre se pueden implementar utilizando filtros no lineales mínimos y máximos, por lo que se aplican las consideraciones anteriores. La reconstrucción morfológica también puede funcionar en nD. Por lo tanto, todas las nuevas operaciones y trucos derivados de estos métodos (por ejemplo, crear contornos, encontrar máximos regionales) deberían funcionar.
Los algoritmos de adelgazamiento suelen estar diseñados para funcionar en 3D, aunque normalmente no en dimensiones más altas.
Tranformada de imagen#
Las transformadas de distancia y watershed se extienden fácilmente al 3D, pero requieren un poco de precaución.
Algo que debe considerarse, especialmente con la transformada de distancia, es si se tiene en cuenta la anisotropía de los píxeles. Si no, la transformada de distancia no será capaz de identificar correctamente el píxel de primer plano o de fondo «más cercano» en unidades calibradas, sino solo en unidades de píxeles.
Una solución engorrosa puede ser cambiar el tamaño de la imagen para que los píxeles sean isotrópicos, pero eso puede hacer que cualquier otro paso del análisis sea más complicado y/o requerir una mayor cantidad de memoria para almacenar la imagen. Un enfoque preferible es tratar de encontrar una implementación de transformación de distancia que incorpore información del tamaño de los píxeles en sus cálculos.
Acelerar el análisis#
Uno de los temas comunes en el procesamiento de imágenes multidimensionales es el rendimiento.
Aunque conceptualmente la mayoría de las técnicas de procesamiento de imágenes que hemos discutido se pueden extender a 3D y más allá, generalmente no es fácil hacerlo desde la perspectiva del programador. Como alguien que escribe software, puedo dar fe de que no tiendo a admitir más dimensiones de las necesarias porque las dimensiones adicionales hacen que la tarea de codificar, depurar y optimizar sea mucho, mucho más difícil.
La «optimización» realmente importa porque, como se mencionó anteriormente, los requisitos computacionales pueden aumentar rápida y dramáticamente con datos multidimensionales. Eso no significa sólo que el software en sí debe optimizarse para funcionar rápidamente: el usuario desempeña un papel muy importante a la hora de elegir lo que le pide al software que haga. Ten en cuenta:
¡La consideración de rendimiento más importante es el algoritmo!
Antes de invertir en una computadora más grande para intentar acelerar un flujo de trabajo de análisis lento, busca formas de hacerlo más eficiente sin comprometer la precisión.
Por ejemplo, ¿realmente necesitas aplicar un filtro de 49×49×49 píxeles a una imagen grande, a un costo de 117,649 multiplicaciones y sumas por cada píxel? Si en su lugar se puede utilizar un filtro separable, se puede reducir esa cifra a 147 (~0,12%). Quizás el cálculo también se pueda realizar en una imagen de menor resolución, ahorrando aún más esfuerzo.
Alternativamente, si descubres que estás aplicando filtros mínimos o máximos grandes a una imagen binaria, tal vez podrías usar una transformación de distancia para erosión y dilatación.
Cuando el procesamiento es lento, vale la pena intentar que la computadora funcione de manera más inteligente, no más intensa.
Sin embargo, llega un momento en que un mejor hardware realmente puede ayudar, suponiendo que el software pueda aprovecharlo.
La mayoría de las computadoras modernas capaces de analizar imágenes contienen múltiples procesadores, que pueden hacer varias cosas al mismo tiempo. El software de análisis de imágenes que admite multiprocesamiento puede utilizar estos procesadores para operar en diferentes partes de los datos simultáneamente. Es más trabajo para el programador, pero mejor para el usuario.
Los beneficios del multiprocesamiento pueden ser importantes, pero aún así tienden a ser bastante modestos. Un ordenador de mesa típico hoy en día podría tener entre 2 y 8 procesadores (aunque las máquinas especialmente potentes pueden tener más). Sin embargo, duplicar el número de procesadores no significa que el tiempo de cálculo se reducirá a la mitad, porque al software le resulta difícil mantener ocupados todos los procesadores. Las tareas tienden a depender unas de otras, por lo que es común que un procesador tenga que holgazanear mientras otro procesador completa su parte del trabajo. Nuestras aspiraciones de rendimiento también pueden verse frustradas por otros obstáculos, como la lectura o la escritura de imágenes.
Para ver una mejora dramática en el rendimiento del procesamiento de imágenes, normalmente debemos analizar las Unidades de procesamiento de gráficos (GPU), también conocidas como. tarjetas gráficas.
Una GPU no puede hacer todo lo que puede hacer un procesador de propósito general, pero es muy buena en lo que puede hacer, lo que incluye operaciones centrales como filtrado de imágenes o multiplicación de matrices.
La programación para GPU es bastante especializada, pero existen algunas herramientas que pueden ayudar. Robert Haase ha trabajado extensamente en el uso de GPU para análisis de bioimágenes multidimensionales. Recomiendo encarecidamente consultar CLIJ y [clEsperanto] (https://clesperanto.github.io) para más detalles.

