Filtros

Outline del capítulo

• El filtrado puede facilitar mucho la segmentación al mejorar las funciones y reducir el ruido

• Filtros lineales reemplazan cada píxel por una suma ponderada de los píxeles circundantes

• Filtros no lineales reemplazan cada píxel con el resultado de otro cálculo utilizando los píxeles circundantes

• Los filtros Gaussianos son filtros lineales con propiedades particularmente útiles, lo que los convierte en una buena opción para muchas aplicaciones.

Show code cell content Hide code cell content

%load_ext autoreload
%autoreload 2

# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage

Introducción

Los filtros son fenomenalmente útiles. Casi todos los análisis de imágenes interesantes implican filtrar de alguna manera en algún momento. De hecho, el análisis de una imagen difícil a veces puede volverse (casi) trivial una vez que se le ha aplicado un filtro adecuado. Por lo tanto, no sorprende que gran parte de la literatura sobre procesamiento de imágenes esté dedicada al tema del diseño y prueba de filtros.

La idea básica del filtrado aquí es que a cada píxel de una imagen se le asigna un nuevo valor dependiendo de los valores de otros píxeles dentro de una región definida (el vecindario del píxel). Los diferentes filtros funcionan aplicando diferentes cálculos a la vecindad para obtener su resultado. Aunque la gran cantidad de filtros disponibles puede resultar intimidante al principio, conocer sólo algunos de los filtros más útiles ya es una gran ventaja.

Este capítulo comienza presentando varios filtros lineales y no lineales extremadamente comunes para el procesamiento de imágenes. El capítulo termina considerando en detalle algunas técnicas basadas en un filtro lineal particularmente importante.

Filtros lineales

Los filtros lineales reemplazan cada píxel con una combinación lineal («suma de productos») de otros píxeles. Por lo tanto, la única base matemática que necesitan es la capacidad de sumar y multiplicar.

Un filtro lineal se define utilizando un núcleo (kernel) de filtro, que es como una imagen pequeña en la que los píxeles se denominan coeficientes de filtro. Para filtrar una imagen, centramos el núcleo sobre cada píxel de la imagen de input. Luego multiplicamos cada coeficiente de filtro por el píxel de la imagen de entrada que se superpone, sumando el resultado para obtener nuestro valor de píxel filtrado. Algunos ejemplos deberían aclarar esto.

Filtros medios

Podría decirse que el filtro lineal más simple es el filtro medio. Cada valor de píxel simplemente se reemplaza por el promedio (media) de sí mismo y de sus vecinos dentro de un área definida.

Un simple filtro de media 3×3 promedia cada píxel con sus 8 vecinos inmediatos (arriba, abajo, izquierda, derecha y diagonales). El núcleo del filtro contiene 9 valores, dispuestos como un cuadrado de 3×3. Cada coeficiente es 1/9, lo que significa que juntos todos los coeficientes suman 1.

El proceso de filtrado con un núcleo de filtro medio de 3×3 se demuestra a continuación:

Uno de los usos principales de un filtro medio de 3×3 es reducir algunos tipos comunes de ruido de imagen, incluyendo el ruido Gaussiano y el ruido de Poisson.

Discutiremos el tema del ruido con mucho más detalle en un capítulo posterior, Ruido, y demostraremos por qué un filtro medio funciona para reducirlo. En este punto, todo lo que necesitamos saber sobre el ruido es que actúa como un error aleatorio (positivo o negativo) agregado a cada valor de píxel, lo que oscurece los detalles, altera el histograma y hace que la imagen parezca granulada.

Figura 82 proporciona un ejemplo de la eficacia con la que el filtro 3×3 puede reducir el ruido Gaussiano en una imagen.

Show code cell content Hide code cell content

from scipy import ndimage
import matplotlib.pyplot as plt

im = load_image('happy_cell.tif').astype(np.float32)
im = im[::2, ::2]
rng = np.random.default_rng(100)
im = im + rng.normal(size=im.shape) * 10

# Identify central row & define how line should be displayed
row = im.shape[0] // 2
line_args = ([0, im.shape[1]-1], [row, row], 'w--')

# Create a 3x3 mean filter kernel
kernel = np.ones((3, 3))
kernel /= kernel.sum()

# Ensure aligned
# fig = create_figure(figsize=(8, 8))
fig, ax = plt.subplots(2, 3, sharex='col', sharey='row', figsize=(8, 5), dpi=200)

# Show images & plots
show_image(im, title="(A) Original image", pos=231)
plt.plot(*line_args)

im_mean = ndimage.convolve(im, kernel)
show_image(im_mean, title="(B) Mean filtered", pos=232)
plt.plot(*line_args)

im_diff = im - im_mean
s = im_diff.std() * 3
show_image(im_diff, title="(C) Subtraction (A) - (B)", vmin=-s, vmax=s, pos=233)
plt.plot(*line_args)

show_plot(im[row, :], ylabel='Value', xlabel='x', pos=234)
show_plot(im_mean[row, :], xlabel='x', pos=235)
show_plot(im_diff[row, :], xlabel='x', pos=236)

plt.tight_layout()
glue_fig('fig_filt_reduce_noise', fig)

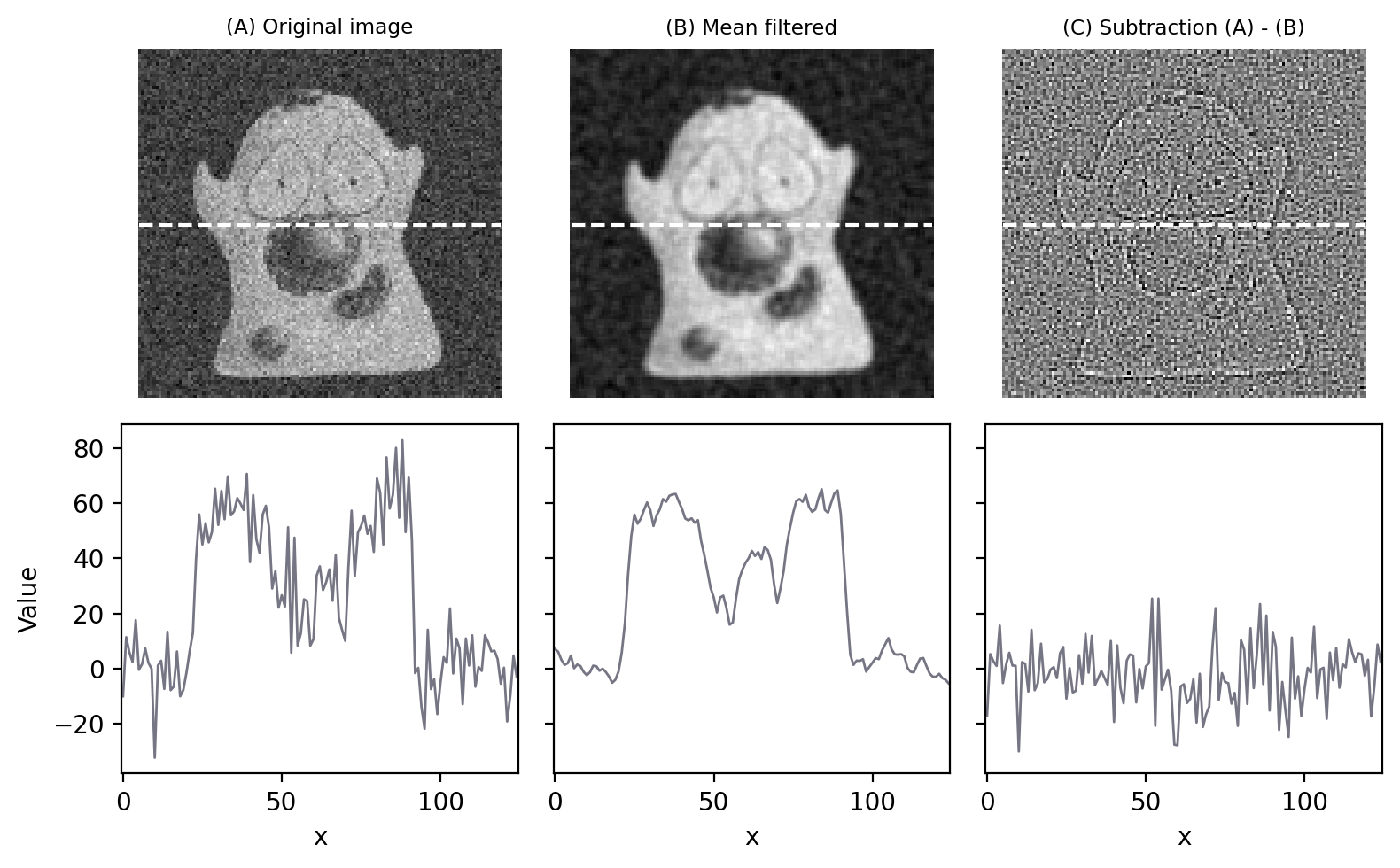
Figura 82 Se pueden utilizar filtros para reducir el ruido. La aplicación de un filtro medio de 3 × 3 hace que la imagen sea más suave, como es particularmente evidente en el gráfico de fluorescencia realizado a través del centro de la imagen. Calcular la diferencia entre imágenes muestra lo que eliminó el filtro, que fue principalmente ruido aleatorio (con un poco de detalle de la imagen también).

Nuestro sencillo filtro medio de 3×3 podría modificarse fácilmente de al menos dos maneras:

1. Se podría aumentar su tamaño. Por ejemplo, en lugar de utilizar sólo los píxeles inmediatamente adyacentes al que nos interesa, un filtro medio de 5×5 reemplaza cada píxel por el promedio de un cuadrado que contiene 25 píxeles, todavía centrado en el píxel principal de interés.

2. Se podría calcular el promedio de los píxeles en algun otro formato de región, no solo un cuadrado n×n.

Ambos ajustes se pueden lograr cambiando el tamaño del núcleo (kernel) del filtro y sus coeficientes.

Un cambio común es hacer un filtro promedio «circular». Podemos hacer esto definiendo el núcleo de tal manera que los coeficientes que queremos ignorar tengan el valor de 0 y los píxeles distintos de cero se aproximen a un círculo. Luego, el tamaño del filtro se define en términos de un valor de radio (Figura 83).

Show code cell content Hide code cell content

fig = create_figure(figsize=(8,4))

def make_disk(radius: float, width=5) -> np.ndarray:
    """
    Use a distance transform to create a circular disk filter
    """
    from scipy.ndimage import distance_transform_edt
    k = np.zeros((width, width), dtype=bool)
    k[width//2, width//2] = 1
    # Different implementations treat the radius value differently...
    # here, we try to match ImageJ's filters for the figure
    return distance_transform_edt(~k) <= radius + 0.5

kernels = [
    ('3x3 square', np.pad(np.ones((3,3)), 1), (0.2, 0.2, 0.7)),
    ('Circular, radius=1.5', make_disk(1.5), (0.2, 0.7, 0.2)),
    ('Circular, radius=2.5', make_disk(2), (0.7, 0.2, 0.2)),
    ('5x5 square', np.ones((5,5)), (0.6, 0.2, 0.6)),
]
colors = [(0.8, 0.2, 0.2)]
ii = 0
from matplotlib.colors import ListedColormap

# Show the kernels + grid (more code than you might expect...)
for name, kernel, c in kernels:
    ii += 1
    if ii == 1:
        show_image(kernel, vmin=0, vmax=1, cmap=ListedColormap([c+(0,), c+(0.4,)]), alpha = 1, title=name, pos=(1,len(kernels),ii))
    else:
        show_image(kernel, vmin=0, vmax=1, cmap=ListedColormap([c+(0.1,), c+(0.4,)]), alpha = 1, title=name, pos=(1,len(kernels),ii))
    s = int(kernel.sum())
    plt.xticks(ticks=np.arange(5)-0.5, labels=[])
    plt.yticks(ticks=np.arange(5)-0.5, labels=[])
    plt.xlim(-0.6, 4.6)
    plt.ylim(-0.6, 4.6)
    fd_main = {'size': 10}
    fd_zero = {'size': 8}
    for (i, j), z in np.ndenumerate(kernel):
        if z == 0:
            t = '0'
            fd = fd_zero
        else:
            t = r'$\frac{1}{'+str(s)+'}$'
            fd = fd_main
        plt.text(j, i, t, ha='center', va='center', fontdict=fd)
        plt.hlines(np.arange(6)-0.5, -0.5, 4.5, color=c+(0.25,), linewidth=0.25)
        plt.vlines(np.arange(6)-0.5, -0.5, 4.5, color=c+(0.25,), linewidth=0.25)
plt.show()

glue_fig('fig_filter_shapes', fig)

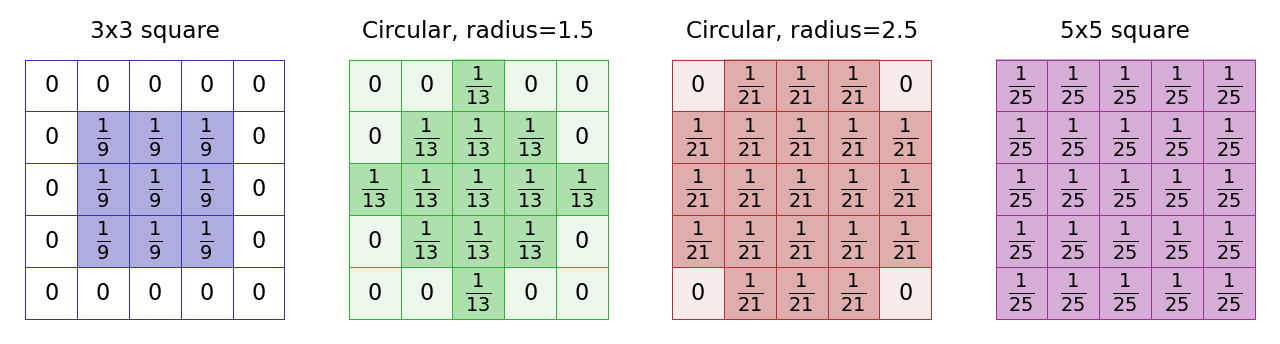
Figura 83 Los nucleos (kernels) se utilizan con varios filtros promedio. Ten en cuenta que no existe una forma claramente «correcta» de aproximar un círculo dentro de una cuadrícula de píxeles y, como resultado, diferentes programas pueden crear filtros circulares que son ligeramente diferentes. Aquí, (B) y (C) coinciden con los filtros “circulares” utilizados por el comando Process ‣ Filters ‣ Mean… de ImageJ.

Diferentes nombres para (casi) lo mismo

El mundo del filtrado está lleno de conceptos con múltiples nombres, y todos significan prácticamente lo mismo. Por ejemplo:

• El filtrado lineal puede denominarse convolución (muy común) o correlación[^fn_conv] (menos común)

• un núcleo (kernel) de filtro podría denominarse máscara de filtro

• Los filtros de media a veces se denominan filtros de media aritmética, filtros de promedio o filtros de furgón

Elige tu opción. Vale la pena conocer la equivalencia para evitar confundirse con la literatura. En particular, “convolve” se utiliza con tanta frecuencia como sinónimo de “filtro” (con un filtro lineal) que es importante recordar.

Aumentar el tamaño de un filtro medio aumenta su impacto. Esto no es solo en términos de reducir el ruido, sino también en términos de reducir los detalles, es decir, hacer que la imagen sea más borrosa (Figura 84). Si el objetivo principal es la reducción de ruido, es mejor evitar la borrosidad innecesaria utilizando el filtro más pequeño que proporcione resultados aceptables.

Show code cell content Hide code cell content

# Create a circular mean filter
def create_mean_kernel(radius: int):
    r = radius
    x = np.arange(-r, r+1)
    y = np.arange(-r, r+1)
    y, x = np.meshgrid(x, x)
    mask = x*x + y*y <= r*r
    kernel = mask.astype(np.float64)
    return kernel / kernel.sum()


from scipy import ndimage
import matplotlib.pyplot as plt

im = load_image('happy_cell.tif').astype(np.float32)
im = im[::2, ::2]
rng = np.random.default_rng(100)
im = im + rng.normal(size=im.shape) * 10

kernels = {
    'Original image': None,
    'Filtered, radius=1': create_mean_kernel(1),
    'Filtered, radius=5': create_mean_kernel(5),
    'Filtered, radius=10': create_mean_kernel(10)
}

# Identify central row & define how line should be displayed
row = im.shape[0] // 2
line_args = ([0, im.shape[1]-1], [row, row], 'w--')

# Ensure aligned
# fig = create_figure(figsize=(8, 8))
fig, ax = plt.subplots(2, len(kernels), sharex='col', figsize=(8, 4), dpi=200)

count = 0
n = len(kernels)
for title, kernel in kernels.items():
    count += 1
    if kernel is None:
        im_filtered = im
    else:
        im_filtered = ndimage.convolve(im, kernel)

    # Show images & plots
    show_image(im_filtered, title=title, pos=(2, n, count))
    plt.plot(*line_args)

    show_plot(im_filtered[row, :], xlabel='x', pos=(2, n, n+count))
    plt.ylim([-20, 80])
    if count > 1:
        plt.yticks([])
    else:
        plt.ylabel('Value')

plt.tight_layout()
glue_fig('fig_mean_filter_sizes', fig)

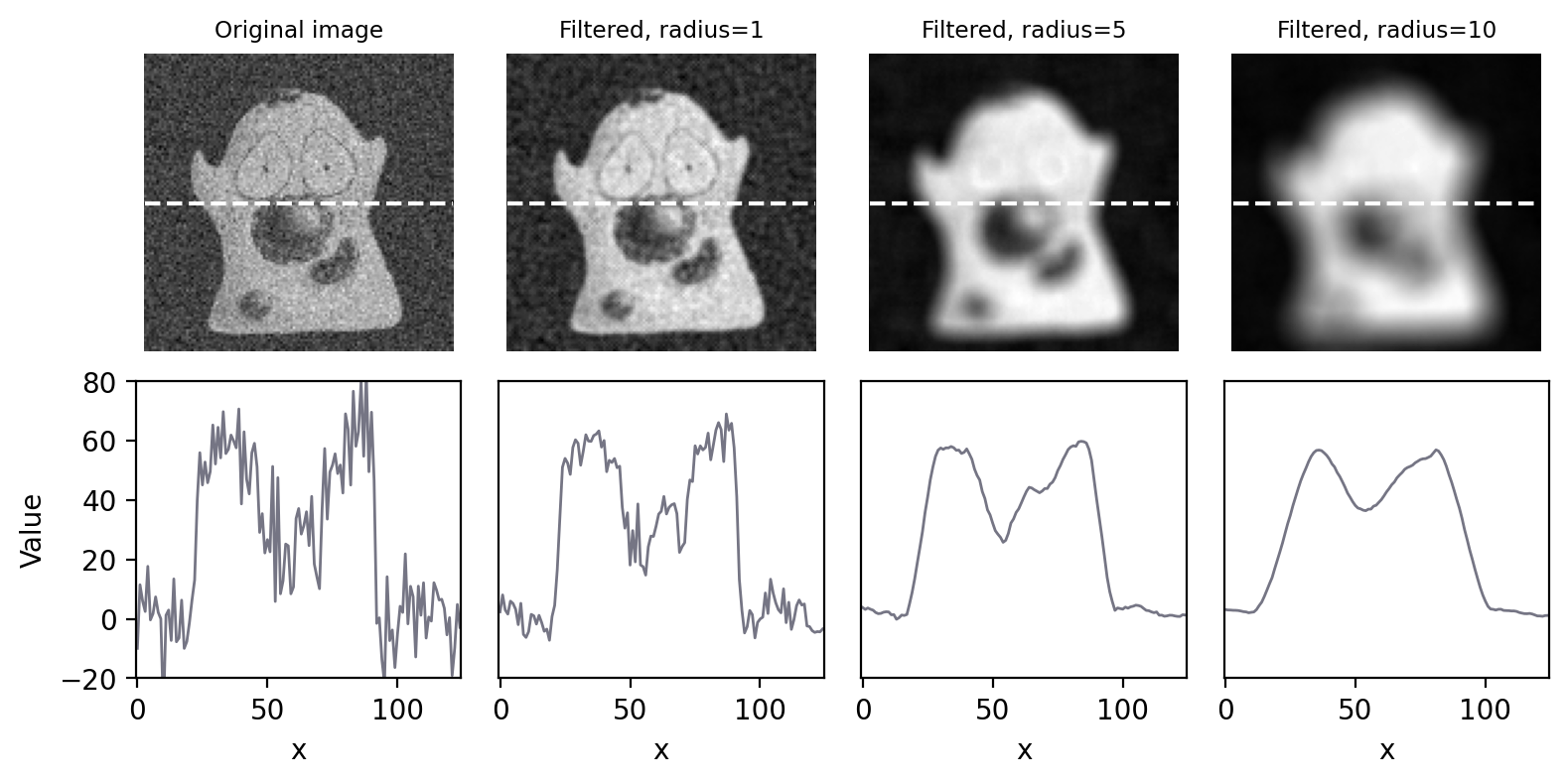
Figura 84 Suavizar una imagen usando filtros medios circulares con diferentes radios.

Pregunta

En ImageJ, crear un filtro medio con Radio = 6 da como resultado un filtro circular que reemplaza cada píxel con la media de 121 píxeles. El uso de un filtro cuadrado de 11 × 11 también reemplazaría cada píxel con la media de 121 píxeles.

¿Se te ocurre alguna ventaja al utilizar el filtro circular en lugar del filtro cuadrado?

Respuesta

Los círculos son más «compactos». Cada punto del perímetro de un círculo está a la misma distancia del centro. Por lo tanto, usar un filtro circular implica calcular la media de todos los píxeles a una distancia de \(\leq\) Radius píxeles del centro.

Para un filtro cuadrado, los píxeles que están más alejados en direcciones diagonales que en direcciones horizontales o verticales pueden influir en los resultados. Si un píxel está más lejos, es más probable que tenga un valor muy diferente porque forma parte de alguna otra estructura. Promediar las estructuras puede difuminarlas entre sí, por lo que es mejor evitarlo.

Filtros de gradiente

Los filtros lineales pueden hacer mucho más que simplemente calcular promedios locales. Solo necesitamos definir un nuevo núcleo de filtro con diferentes coeficientes.

A menudo queremos detectar estructuras en una imagen que se distinguen del fondo por sus bordes. Por lo tanto, poder detectar los bordes podría resultar útil. Debido a que un borde generalmente se caracteriza por una transición relativamente nítida en los valores de píxeles, es decir, por un aumento o disminución pronunciados en el perfil en la imagen, se pueden utilizar filtros de gradiente para ayudar.

Un filtro de gradiente muy simple tiene los coeficientes -1, 0, 1. Aplicado a una imagen, esto reemplaza cada píxel con la diferencia entre el píxel de la derecha y el píxel de la izquierda. El output es positivo siempre que los valores de los píxeles aumentan horizontalmente, negativo cuando los valores de los píxeles disminuyen y cero si los valores son constantes, sin importar cuál era el valor constante original, de modo que las áreas planas son cero en la imagen de gradiente independientemente de su brillo original. También podemos rotar el filtro 90 grados y obtener una imagen con gradiente vertical (Figura 85).

Show code cell content Hide code cell content

fig = create_figure(figsize=(8, 4))

im = load_image('happy_cell.tif')

kernel_horizontal = np.asarray([-1, 0, 1]).reshape((1, 3))
kernel_vertical = np.asarray([-1, 0, 1]).reshape((3, 1))

im_horizontal = ndimage.convolve(im, kernel_horizontal)
show_image(im_horizontal, title="(A) Horizontal gradient", pos=131)

im_vertical = ndimage.convolve(im, kernel_vertical)
show_image(im_vertical, title="(B) Vertical gradient", pos=132)

im_grad_mag = np.sqrt(im_horizontal*im_horizontal + im_vertical*im_vertical)
show_image(im_grad_mag, title="(C) Gradient magnitude", pos=133)

glue_fig('fig_processing_filters_gradient', fig)

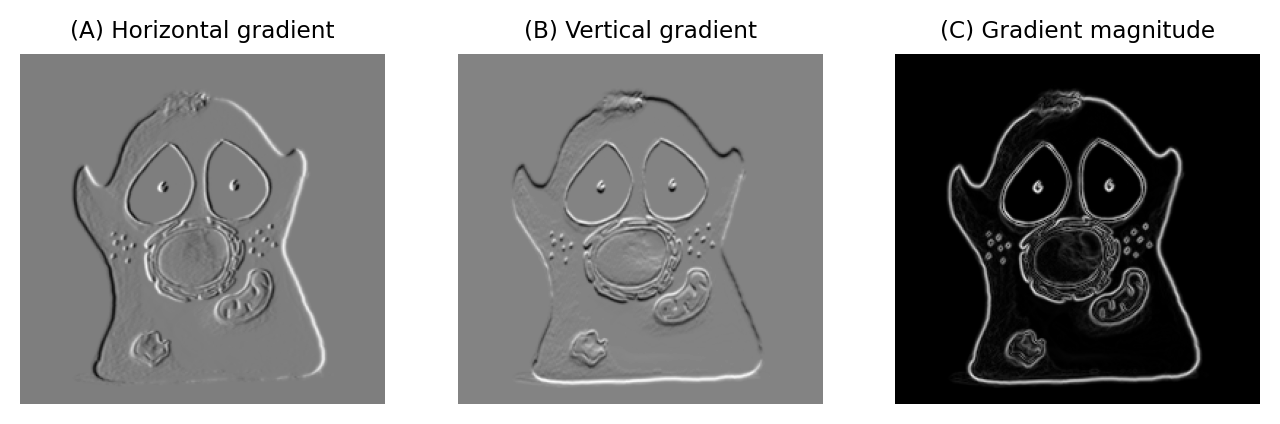
Figura 85 Uso de filtros de gradiente y la magnitud del gradiente para mejorar los bordes.

Puede resultar algo difícil trabajar con dos imágenes con gradientes, con valores positivos y negativos. Podemos combinar el filtrado con [operaciones puntuales] (chap_point_operations) para generar una única imagen que represente la magnitud del gradiente [^fn_3]. La magnitud del gradiente tiene valores altos alrededor de los bordes (independientemente de su orientación) y valores bajos en el resto.

El proceso de calcular la magnitud del gradiente es:

• Aplica filtros lineales para producir imágenes de gradiente horizontal y vertical.

• Eleva al cuadrado todos los valores de píxeles en ambas imágenes de gradiente

• Suma las imágenes cuadradas juntas

• Saca la raíz cuadrada del resultado.

Pregunta

Supongamos que el valor medio de píxeles de una imagen es 100. ¿Cuál será el valor medio después de aplicar un filtro de gradiente horizontal?

Solución

Después de aplicar un filtro de gradiente, la media de la imagen será 0: cada píxel se suma una vez y se resta una vez al calcular el resultado.

(Ten en cuenta que el valor medio de una imagen de magnitud de gradiente será ≥ 0, porque todos los píxeles tienen valores positivos o son iguales a cero).

Filtrado en los límites de la imagen

Si un filtro consta de más de un coeficiente, la vecindad se extenderá más allá de los límites de la imagen al filtrar algunos píxeles cercanos. Necesitamos manejar esto de alguna manera. Hay varias formas de hacerlo.

Los píxeles de los límites podrían simplemente ignorarse y dejarse con sus valores originales, pero en vecindarios grandes esto daría como resultado que gran parte de la imagen no estuviera filtrada. Las opciones alternativas incluyen tratar cada píxel más allá del límite como cero, replicar el píxel válido más cercano, tratar la imagen como si fuera parte de un mosaico periódico o reflejar los valores internos ({numref} fig-filter_boundaries).

Show code cell content Hide code cell content

"""
Illustrate different boundary padding methods that may be used with convolution.
"""

fig = create_figure(figsize=(8, 4))

im = load_image('/images/boundary_demo.png')
pad_size = 100

im_padded = np.pad(im, pad_size, mode='constant', constant_values=im.max())
show_image(im_padded, title="(A) Original image", pos=231)

im_zeros = np.pad(im, pad_size, mode='constant')
show_image(im_zeros, title="(B) Zeros", pos=232)

im_replicate = np.pad(im, pad_size, mode='edge')
show_image(im_replicate, title="(C) Edge replication", pos=233)

im_circular = np.pad(im, pad_size, mode='wrap')
show_image(im_circular, title="(D) Wrapped/circular", pos=234)

im_symmetric = np.pad(im, pad_size, mode='symmetric')
show_image(im_symmetric, title="(E) Symmetric", pos=235)

im_extra = np.pad(im, pad_size, mode='linear_ramp')
show_image(im_extra, title="(E) Linear ramp", pos=236)

glue_fig('fig_filter_boundaries', fig)

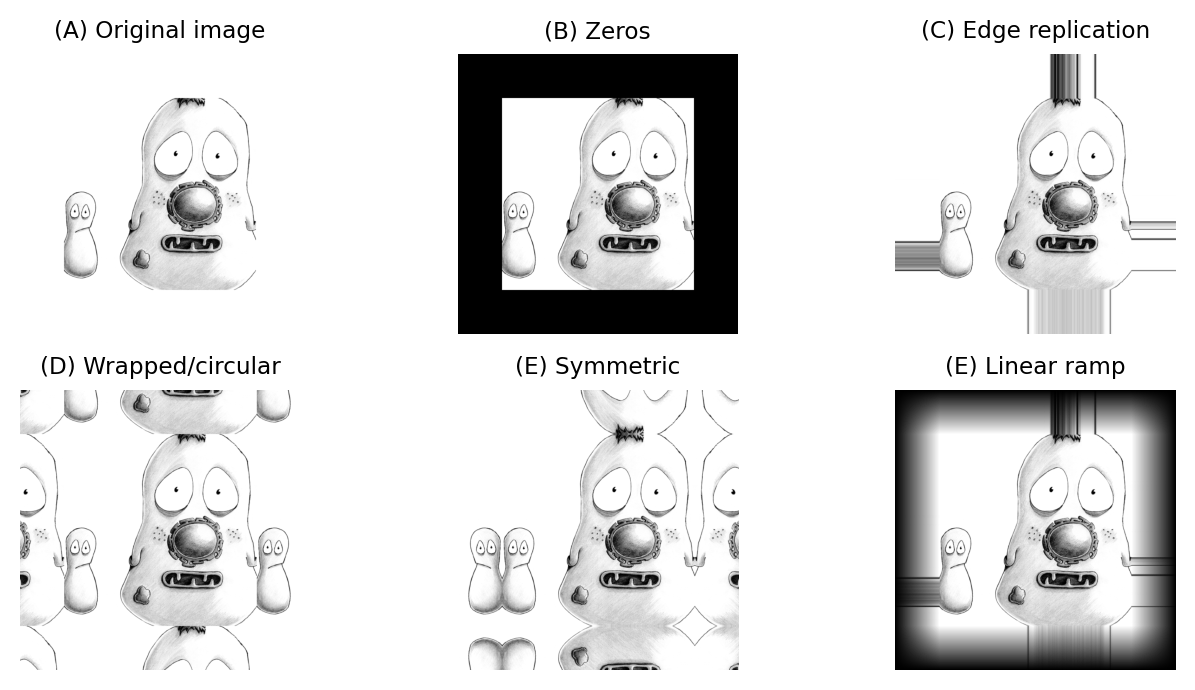
Figura 86 Métodos para determinar valores adecuados para píxeles más allá de los límites de la imagen al filtrar.

Cada software puede manejar los límites de diferentes maneras. A menudo, si utiliza una biblioteca de procesamiento de imágenes para codificar su propia operación de filtrado, podrá especificar la operación de límite.

Filtros no lineales

Los filtros lineales implican tomar vecindades de píxeles, escalarlos según los coeficientes del filtro y sumar los resultados para obtener nuevos valores de píxeles. Los filtros no lineales también utilizan vecindades de píxeles, pero pueden utilizar cualquier otro tipo de cálculo para obtener el resultado. Aquí consideraremos una familia especialmente importante de filtros no lineales.

Filtros de clasificación

Clasificar filtros clasifica efectivamente los valores de todos los píxeles vecinos en orden ascendente y luego elige el output según esta lista ordenada.

Quizás el ejemplo más común sea el filtro mediano, en el que el valor de píxel en el centro de la lista se utiliza para el output filtrado.

Figura 87 Resultados de diferentes filtros de rango 3×3 al procesar un solo vecindario en una imagen. La salida de un filtro medio de 3×3 en este caso también sería 15.

El resultado de aplicar un filtro de mediana suele ser similar al de aplicar un filtro de media, pero tiene la principal ventaja de eliminar por completo los valores extremos aislados, sin permitir que tengan un impacto en los píxeles circundantes. Esto contrasta con un filtro medio o promedio, que no puede ignorar los píxeles extremos, sino que los suaviza para ocupar regiones más grandes (Figura 88).

Sin embargo, una desventaja de un filtro mediano es que puede parecer que introduce patrones o texturas que no estaban presentes en la imagen original, al menos cada vez que aumenta el tamaño del filtro (ver Figura 92D a continuación). Otra desventaja es que los filtros medianos grandes tienden a ser lentos.

Show code cell content Hide code cell content

"""
Illustrate how median filters remove salt-and-pepper noise more cleanly than mean filters.
(Note: most noise isn't like this, and median filters aren't always preferable)
"""

fig = create_figure(figsize=(8, 4))

from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes

def add_inset(ax, im, loc=[50, 50, 160, 160], edge_color='black', **kwargs):
    axins = zoomed_inset_axes(ax, zoom=4, loc='upper left')
    x = 340
    y = 210
    s = 40
    axins.imshow(im, cmap='gray', interpolation='nearest', **kwargs)
    axins.set_xlim(x, x+s)
    axins.set_ylim(y+s, y)
    axins.set_xticks([])
    axins.set_yticks([])
    ax.indicate_inset_zoom(axins, edgecolor=edge_color)


im = load_image('fixed_cells.png')

# Add salt-and-pepper noise by creating uniformly distributed noise,
# then thresholding to choose which pixels should become black and white
threshold = 0.05
rng = np.random.default_rng(100)
im_random = rng.random(size=im.shape)
im[im_random < threshold] = 0
im[im_random > 1-threshold] = 255
show_image(im, title="(A) Salt & pepper noise", pos=131, origin="upper")
add_inset(plt.gca(), im)

# 3x3 mean filter
kernel = np.ones((3, 3))
kernel = kernel / kernel.sum()
im_mean = ndimage.convolve(im, kernel)
show_image(im_mean, title="(B) Mean filter", pos=132)
add_inset(plt.gca(), im_mean)

# 3x3 median filter
im_median = ndimage.median_filter(im, size=3)
show_image(im_median, title="(C) Median filter", pos=133)
add_inset(plt.gca(), im_median)

glue_fig('fig_processing_filters_speckled', fig)

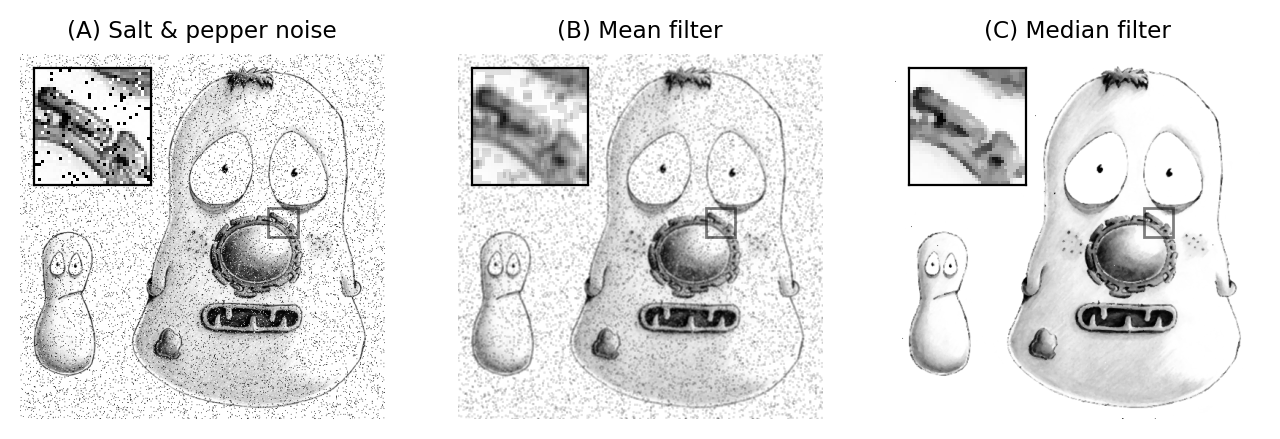
Figura 88 Aplicar filtros de media y mediana de 3 × 3 a una imagen que contiene valores extremos aislados (conocido como ruido de sal y pimienta). Un filtro medio reduce la intensidad de los valores extremos pero extiende su influencia. Un pequeño filtro mediano es capaz de eliminar los valores atípicos por completo, con un efecto mínimo sobre el resto de la imagen.

Otros filtros de clasificación incluyen los filtros mínimo y máximo, que reemplazan cada valor de píxel con el valor mínimo o máximo en el vecindario circundante respectivamente (Figura 89). Se volverán más importantes cuando analicemos [operaciones morfológicas] (chap_morph).

Show code cell content Hide code cell content

"""
Compare median, maximum and minimum filters.
"""

fig = create_figure(figsize=(8, 4))

im = load_image('fixed_cells.png')

filt_size = 3
im_median = ndimage.median_filter(im, size=filt_size)
im_max = ndimage.maximum_filter(im, size=filt_size)
im_min = ndimage.minimum_filter(im, size=filt_size)

show_image(im_median, title="(A) Median filter", pos=131)
add_inset(plt.gca(), im_median)
show_image(im_max, title="(B) Maximum filter", pos=132)
add_inset(plt.gca(), im_max)
show_image(im_min, title="(C) Minimum filter", pos=133)
add_inset(plt.gca(), im_min)
glue_fig('fig_processing_filters_rank', fig)

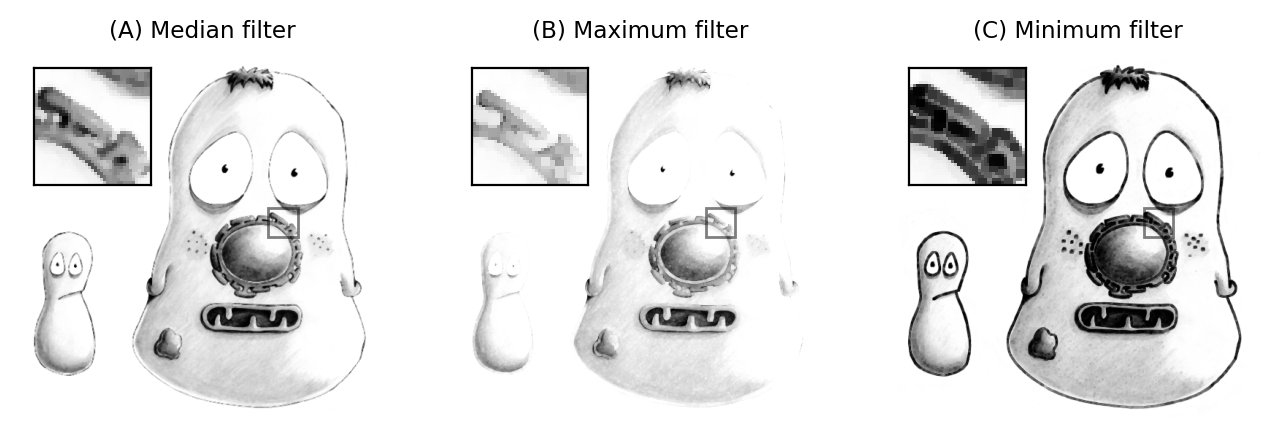
Figura 89 El resultado de aplicar filtros de rango 3×3. La imagen original sin ruido se muestra a continuación en Figura 92A.

Show code cell content Hide code cell content

"""
Compute maximum minus minimum to show it enhances edges.
"""

fig = create_figure(figsize=(2, 2))

im = load_image('fixed_cells.png')

filt_size = 3
im_max = ndimage.maximum_filter(im, size=filt_size)
im_min = ndimage.minimum_filter(im, size=filt_size)

show_image(im_max - im_min)
glue_fig('fig_filters_max_minus_min', fig)

Pregunta

¿Qué pasaría si restas una imagen filtrada mínima (por ejemplo, Figura 89C) de una imagen filtrada máxima (Figura Figura 89B)?

Respuesta

Restar un mínimo de una imagen filtrada máxima sería otra forma de acentuar los bordes:

Filtros Gaussianos

Filtros de funciones Gaussianas

Concluimos este capítulo con un filtro lineal increíblemente importante y algunas variantes basadas en él.

Un filtro Gaussiano es un filtro lineal que también suaviza una imagen y reduce el ruido. Sin embargo, a diferencia de un filtro medio, en el que incluso los píxeles más alejados de la vecindad influyen en el resultado en la misma medida que los píxeles más cercanos, el suavizado de un filtro Gaussiano se pondera de modo que la influencia de un píxel disminuye con su distancia. del centro de filtrado. Esto tiende a dar un mejor resultado en muchos casos (Figura 90).

Show code cell content Hide code cell content

"""
Illustrate difference in mean & Gaussian filter.
Note that filter sizes here are a matter of taste -- there's nothing special about the values.
"""

fig = create_figure(figsize=(8, 4))

# Create a simple image with some points
n = 10
im = np.zeros((n, n))
im[0, 6] = 3
im[5, 0] = 2
im[9, 9] = 1
im = np.pad(im, 10)

show_image(im, pos=131)

# Create Mean filter
kernel = create_mean_kernel(6)
im_mean = ndimage.convolve(im, kernel)
show_image(im_mean, pos=132)

# Create a Gaussian filter
im_gauss = ndimage.gaussian_filter(im, 4)
show_image(im_gauss, pos=133)

glue_fig('fig_filt_smoothing', fig)

Figura 90 Comparación de un filtro medio y gaussiano. El filtro medio (promedio) puede introducir patrones y máximos donde antes no los había. Por ejemplo, la región más brillante en (B) es uno de esos máximos – ¡pero los valores de todos los píxeles en la misma región en (A) eran cero! Por el contrario, el filtro Gaussiano produce un resultado más suave y visualmente más agradable, algo menos propenso a este efecto (C).

Los coeficientes de un filtro Gaussiano se determinan a partir de una función Gaussiana (Figura 91)

\[ g(x, y) = Ae^{-(\frac{x^2 + y^2}{2\sigma^2})} \]

El factor de escala \(A\) se utiliza para hacer que todo el volumen debajo de la superficie sea igual a 1. En términos de filtrado, esto significa que los coeficientes suman 1 y la imagen no se escalará inesperadamente. El tamaño de la función está controlado por \(\sigma\), en lugar de un radio de filtro. \(\sigma\) es equivalente a la desviación estándar de una distribución normal (es decir, Gaussiana).

Show code cell content Hide code cell content

"""
Create a surface plot of a 2D Gaussian function.
"""

from matplotlib import colormaps
from matplotlib.colors import LightSource

n = 50
x = np.arange(-n, n+1, 1)
y = np.arange(-n, n+1, 1)
x, y = np.meshgrid(x, y)

sigma = 10
z = np.exp(-(x*x + y*y)/(2*sigma*sigma))

ls = LightSource()
z = z / z.max()
rgb = ls.shade(z, cmap=colormaps['plasma'], blend_mode='soft')

# Create surface plots
surf_args = dict(
    facecolors = rgb,
    antialiased = False,
    linewidth = 0,
    shade = False,
    rstride = 1,
    cstride = 1
)
fig, ax = plt.subplots(1, 1, subplot_kw=dict(projection='3d', elev=30), dpi=200, figsize=(4, 3))
fig.patch.set_alpha(0.0)
ax.patch.set_alpha(0.0)
ax.plot_surface(x, y, z, **surf_args)
ax.axis(False)

glue_fig('fig_filters_math_gaussian_2d', fig)

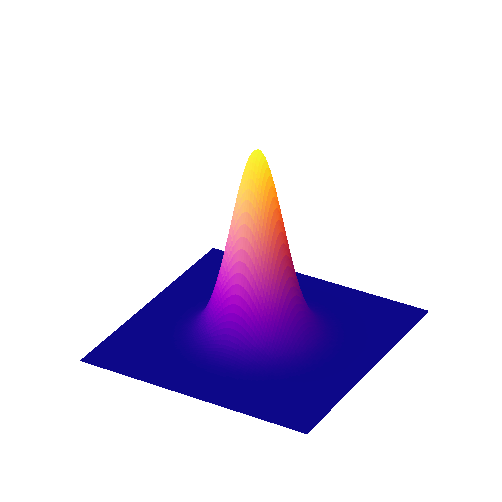
Figura 91 Gráfico de superficie de una función Gaussiana 2D.

Se muestra una comparación de varios filtros en Figura 92.

Show code cell content Hide code cell content

fig = create_figure(figsize=(8, 12))

im = load_image('fixed_cells.png').astype(np.float32) / 255
rng = np.random.default_rng(100)
im_noisy = im + rng.normal(size=im.shape) / 8

show_args = dict(
    vmin = np.percentile(im_noisy, 1),
    vmax = np.percentile(im_noisy, 99)
)

show_image(im, title="(A) Original, noise-free image", pos=321)
add_inset(plt.gca(), im)

show_image(im_noisy, title="(B) Noisy image", **show_args, pos=322)
add_inset(plt.gca(), im_noisy, **show_args)

kernel = create_mean_kernel(3)
im_mean = ndimage.convolve(im_noisy, kernel)
show_image(im_mean, title="(C) Mean filtered, radius = 3", **show_args, pos=323)
add_inset(plt.gca(), im_mean, **show_args)

im_median = ndimage.median_filter(im_noisy, footprint=kernel > 0)
show_image(im_median, title="(D) Median filtered, radius = 3", **show_args, pos=324)
add_inset(plt.gca(), im_median, **show_args)

im_gauss_1 = ndimage.gaussian_filter(im_noisy, 1)
show_image(im_gauss_1, title="(E) Gaussian filtered, $\sigma = 1$", **show_args, pos=325)
add_inset(plt.gca(), im_gauss_1, **show_args)

im_gauss_4 = ndimage.gaussian_filter(im_noisy, 3)
show_image(im_gauss_4, title="(F) Gaussian filtered, $\sigma = 3$", **show_args, pos=326)
add_inset(plt.gca(), im_gauss_4, **show_args)

glue_fig('fig_processing_filters', fig)

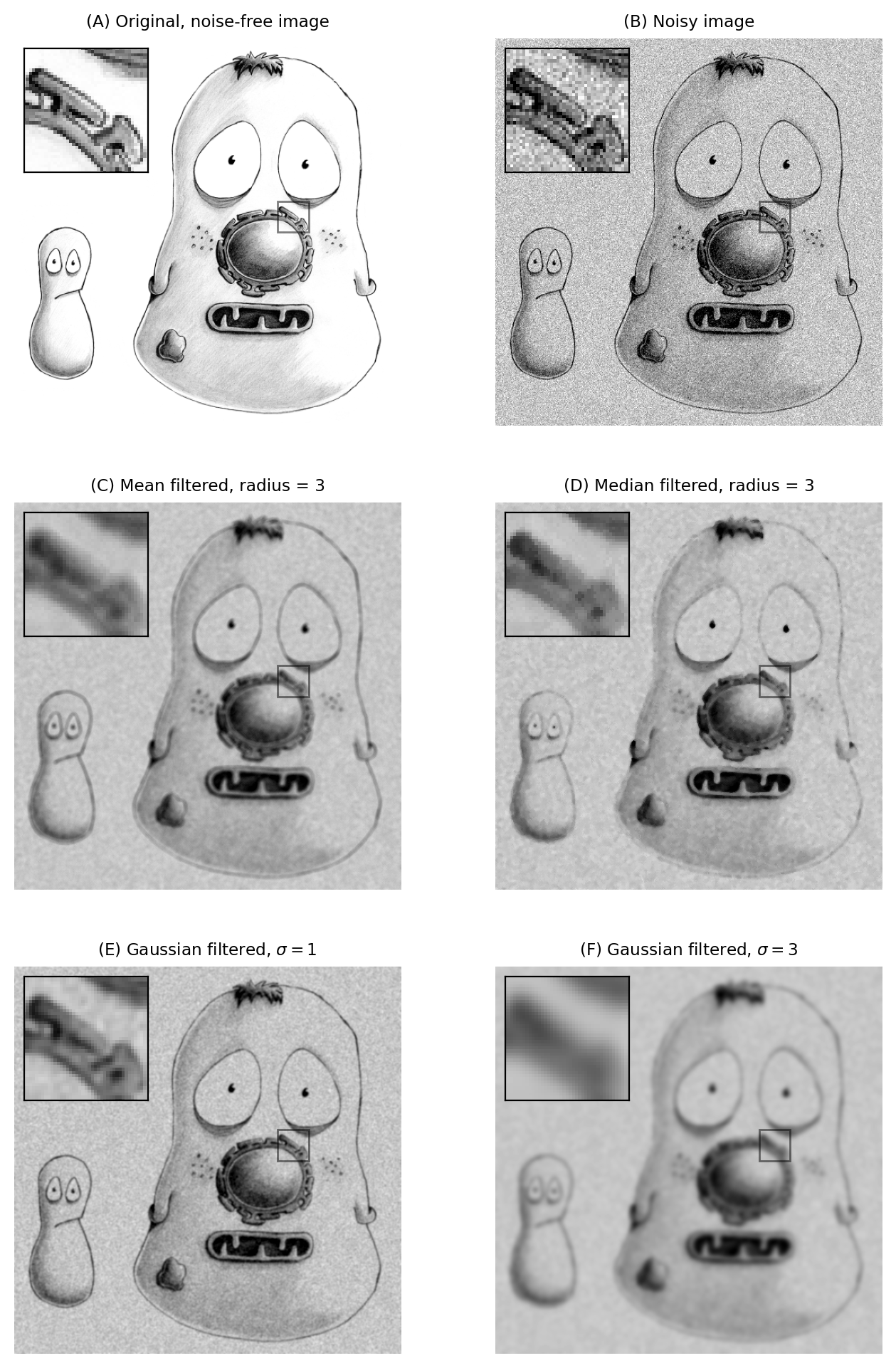
Figura 92 Los efectos de varios filtros sobre una imagen ruidosa de una célula fija.

Filtros de diferentes tamaños.

Los filtros Gaussianos tienen propiedades útiles que los hacen generalmente preferibles a los filtros medios, algunos de los cuales se mencionarán en Desenfoque y Función de dispersión de punto (Point Spread Function o PSF por sus siglas en inglés) (otros requieren un viaje al espacio de Fourier, más allá del alcance de este libro). Por lo tanto, si no estás seguro de qué filtro usar para suavizar, es probable que el Gaussiano sea una opción más segura que la media, especialmente si el filtro es grande. Sin embargo, tus decisiones no han terminado, ya que aún es necesario elegir el tamaño preciso del filtro.

Un filtro pequeño suprimirá principalmente el ruido, porque el ruido se disfraza como pequeñas fluctuaciones aleatorias en píxeles individuales. A medida que aumenta el tamaño del filtro, el filtrado gaussiano comienza a suprimir estructuras más grandes que ocupan múltiples píxeles, reduciendo sus intensidades y aumentando sus tamaños, hasta que finalmente se suavizan en las regiones circundantes ( fig-gaussian_effects). Al variar el tamaño del filtro, podemos decidir la escala en la que debe realizarse el procesamiento y el análisis.

Show code cell content Hide code cell content

# Read image, extract first channel & crop a bit
x = 40
y = 168
w = 100
im = load_image('hela-cells.zip')[y:y+w, x:x+w, 0]

from scipy import ndimage
import matplotlib.pyplot as plt

sigmas = [0, 1, 2, 4]

# Identify central row & define how line should be displayed
row = im.shape[0] // 2
line_args = ([0, im.shape[1]-1], [row, row], 'w--')

# Ensure aligned
# fig = create_figure(figsize=(8, 8))
fig, ax = plt.subplots(2, len(sigmas), sharex='col', figsize=(8, 4), dpi=200)

n = len(sigmas)
for count, sigma in enumerate(sigmas):
    if sigma:
        im_filtered = ndimage.gaussian_filter(im, sigma)
        title = f'Gaussian filtered $\sigma={sigma}$'
    else:
        im_filtered = im
        title = 'Original image'

    # Show images & plots
    show_image(im_filtered, title=title, pos=(2, n, count+1))
    plt.plot(*line_args)

    show_plot(im_filtered[row, :], xlabel='x', pos=(2, n, n+count+1))
    plt.ylim([0, 2200])
    plt.grid(True, axis='y', alpha=0.5)
    if count > 0:
        plt.yticks(ticks=np.arange(500, 2001, 500), labels=[])
    else:
        plt.yticks(ticks=np.arange(500, 2001, 500))
        plt.ylabel('Value')

plt.tight_layout()
glue_fig('fig_gaussian_effects', fig)



# fig = create_figure(figsize=(8, 4))
# show_image('images/gaussian_effects_sigma_0.png', title="(A) Original image", pos=231)
# show_image('images/gaussian_effects_sigma_2.png', title="(B) Gaussian $\sigma = 2$", pos=232)
# show_image('images/gaussian_effects_sigma_5.png', title="(C) Gaussian $\sigma = 5$", pos=233)

# show_image('images/gaussian_effects_plot.png', title="(D) Profile plots of the intensity in the red channel of the image", pos=234)
# glue_fig('fig_gaussian_effects', fig)

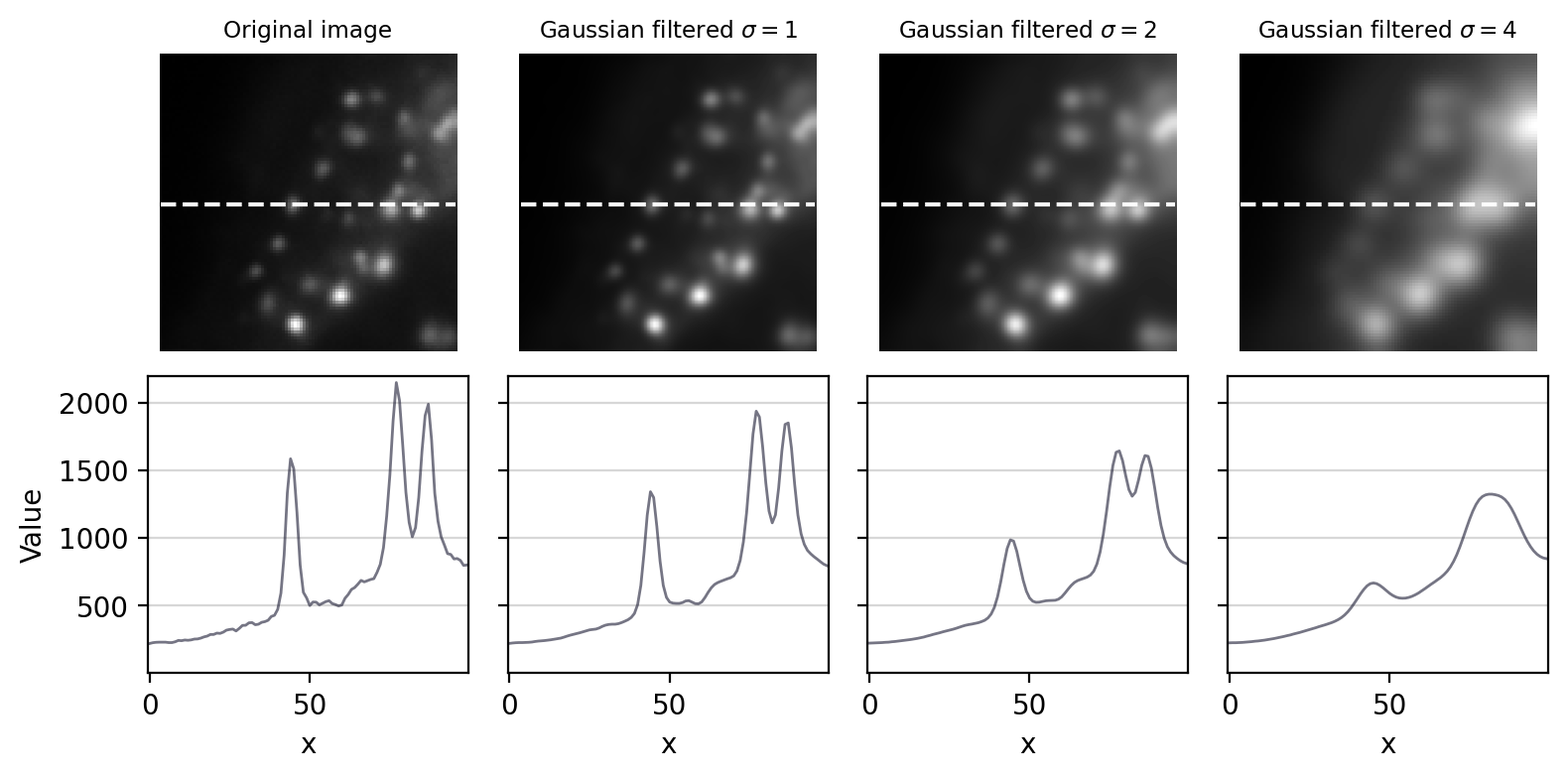
Figura 93 El efecto del filtrado Gaussiano sobre el tamaño y la intensidad de las estructuras.

Figura 94 muestra un ejemplo de cuándo esto es útil. Aquí, se calculan imágenes de magnitud de gradiente, similar a lo que se mostró en Figura 85, pero debido a que la imagen original ahora tiene ruido, el resultado inicial no es muy útil. incluso los bordes más fuertes quedan enterrados en medio del ruido (B). La aplicación de un pequeño filtro Gaussiano antes de calcular la magnitud del gradiente da resultados mucho mejores (C). Si solo queremos los bordes más fuertes, sería mejor aplicar un filtro más grande (D).

Show code cell content Hide code cell content

fig = create_figure(figsize=(8, 4))

def grad_mag(im):
    """
    Calculate a gradient magnitude image
    """
    kernel_h = np.asarray([-1, 0, 1]).reshape((1, 3))
    kernel_v = np.asarray([-1, 0, 1]).reshape((3, 1))
    im_h = ndimage.convolve(im, kernel_h)
    im_v = ndimage.convolve(im, kernel_v)
    return np.sqrt(im_h*im_h + im_v*im_v)

# Get a noisy image
im = load_image('happy_cell.tif')
rng = np.random.default_rng(100)
im = im + rng.normal(size=im.shape) * 10

# Compute gradient magnitude with / without smoothing
im_sigma_0 = grad_mag(im)
im_sigma_2 = grad_mag(ndimage.gaussian_filter(im, 2))
im_sigma_5 = grad_mag(ndimage.gaussian_filter(im, 5))


show_image(im, title="(A) Original image", pos=141)
show_image(im_sigma_0, title="(B) No smoothing", clip_percentile=1, pos=142)
show_image(im_sigma_2, title="(C) Gaussian $\sigma=2$", pos=143)
show_image(im_sigma_5, title="(D) Gaussian $\sigma=5$", pos=144)
glue_fig('fig_edge_sigma', fig)

Figura 94 La aplicación de filtros gaussianos antes de calcular la magnitud del gradiente cambia la escala en la que se mejoran los bordes.

Diferencia de filtrado Gaussiano

Por tanto, se pueden elegir filtros Gaussianos para suprimir estructuras pequeñas. Pero ¿qué pasa si también deseamos suprimir estructuras grandes, para poder concentrarnos en detectar o medir estructuras con tamaños dentro de un rango particular?

Ya tenemos las piezas necesarias para construir una solución.

Supongamos que aplicamos un filtro Gaussiano para reducir estructuras pequeñas. Luego aplicamos un segundo filtro Gaussiano, más grande que el primero, a un duplicado de la imagen original. Esto eliminará aún más estructuras y, al mismo tiempo, conservará las características más grandes de la imagen.

El truco es que, si restamos esta segunda imagen filtrada de la primera, nos queda una imagen que contiene la información que «se encuentra entre» las dos escalas de suavizado que utilizamos.

Este proceso se llama filtrado por diferencia de Gaussianos (DoG) y es una técnica que uso todo el tiempo. Es especialmente útil para detectar estructuras pequeñas o como alternativa a la magnitud del gradiente para mejorar bordes (Figura 95).

Show code cell content Hide code cell content

fig = create_figure(figsize=(6, 6))

def dog_filter(im, sigma1, sigma2):
    """
    Apply a difference of Gaussians filter
    """
    im1 = ndimage.gaussian_filter(im.astype(np.float32), sigma1)
    im2 = ndimage.gaussian_filter(im.astype(np.float32), sigma2)
    return im1 - im2

# Read image, extract first channel & crop a bit
x = 40
y = 40
im = load_image('hela-cells.zip')[y:y+446, x:x+446, 0]

show_image(im, title="(A) Original image", clip_percentile=0.5, pos=221)
show_image(dog_filter(im, 1, 2), title="(B) DoG, $\sigma = $1, 2", clip_percentile=0.5, pos=222)
show_image(dog_filter(im, 2, 4), title="(B) DoG, $\sigma = $2, 4", clip_percentile=0.5, pos=223)
show_image(dog_filter(im, 4, 8), title="(B) DoG, $\sigma = $4, 8", clip_percentile=0.5, pos=224)
glue_fig('fig_dog_red_hela', fig)

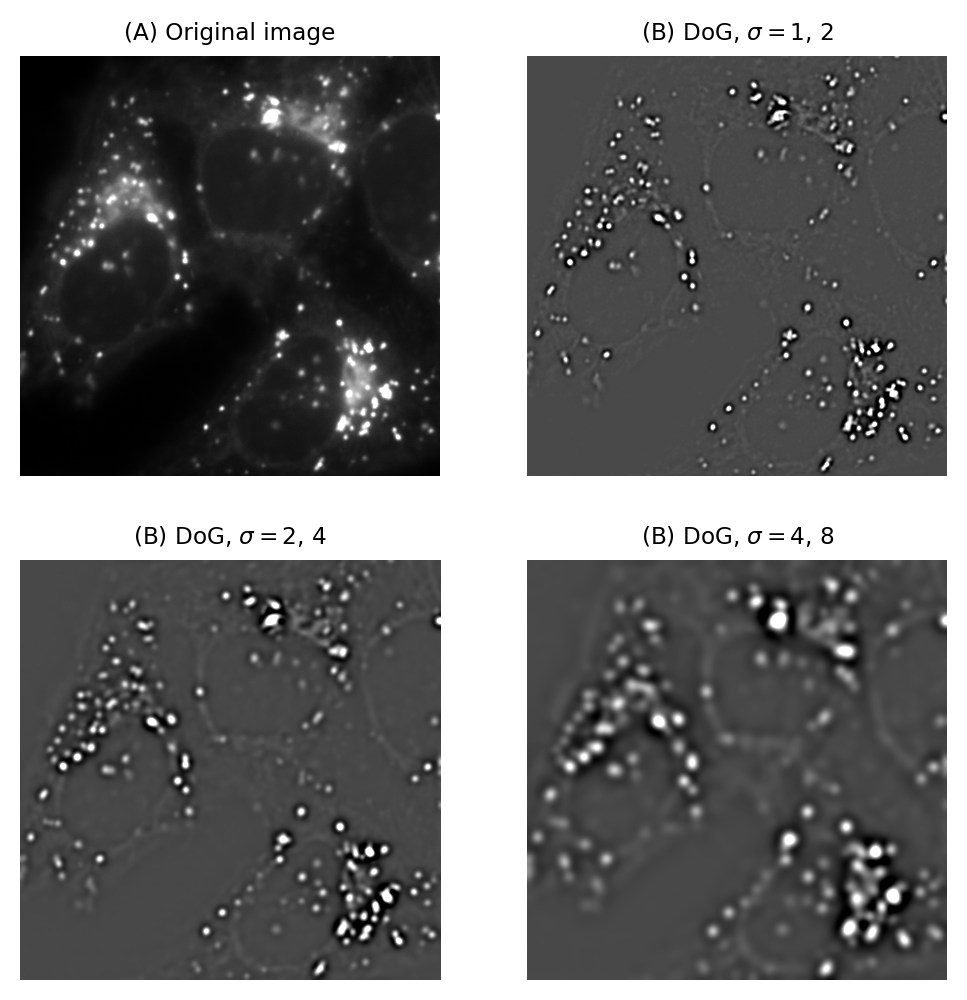
Figura 95 Diferencia del filtrado Gaussiano de la misma imagen en varias escalas.

Show code cell content Hide code cell content

def gaussian_kernel(shape, sigma: float):
    """
    Create an image with a single 1 in the middle,
    the apply a Gaussian filter to get the coefficients.
    """
    filt = np.zeros(shape)
    filt[shape[0]//2, shape[1]//2] = 1.0
    return ndimage.gaussian_filter(filt, sigma)


from matplotlib import colormaps

n = 25
x = np.arange(-n, n+1, 1)
y = np.arange(-n, n+1, 1)
x, y = np.meshgrid(x, y)

# Define filter sigmas
sigma_small = 5
sigma_large = sigma_small * 1.6

# To view the filter coefficients, apply the filter to an image with a single 1
gauss_small = gaussian_kernel(x.shape, sigma_small)
gauss_large = gaussian_kernel(x.shape, sigma_large)
gauss_diff = gauss_small - gauss_large

# Create surface plots
surf_args = dict(
    cmap = colormaps['plasma'],
    antialiased = False,
)
fig, ax = plt.subplots(1, 3, dpi=200, subplot_kw=dict(projection='3d', elev=25), figsize=(15, 5))
ax[0].plot_surface(x, y, gauss_small, **surf_args)
ax[1].plot_surface(x, y, gauss_large, **surf_args)
ax[2].plot_surface(x, y, gauss_diff, **surf_args)

ax[0].set_title('(A) Smaller Gaussian filter')
ax[1].set_title('(B) Larger Gaussian filter')
ax[2].set_title('(C) Difference of Gaussians filter')

# Set z-limits to match
max_val = gauss_small.max()
min_val = gauss_diff.min()
for a in ax:
    a.set_zlim(min_val, max_val)
    a.set_xticklabels([])
    a.set_yticklabels([])
    a.set_zticklabels([])

glue_fig('fig_dog_plots', fig)

Filtrado por Diferencia de Gaussianos (DoG)

De hecho, para obtener el resultado del filtrado DoG no es necesario filtrar la imagen dos veces y restar los resultados. También podríamos restar primero los coeficientes del filtro más grande del más pequeño (después de asegurarnos de que ambos filtros tengan el mismo tamaño agregando ceros a los bordes según sea necesario), luego aplicamos el filtro resultante a la imagen solo una vez (Figura 96).

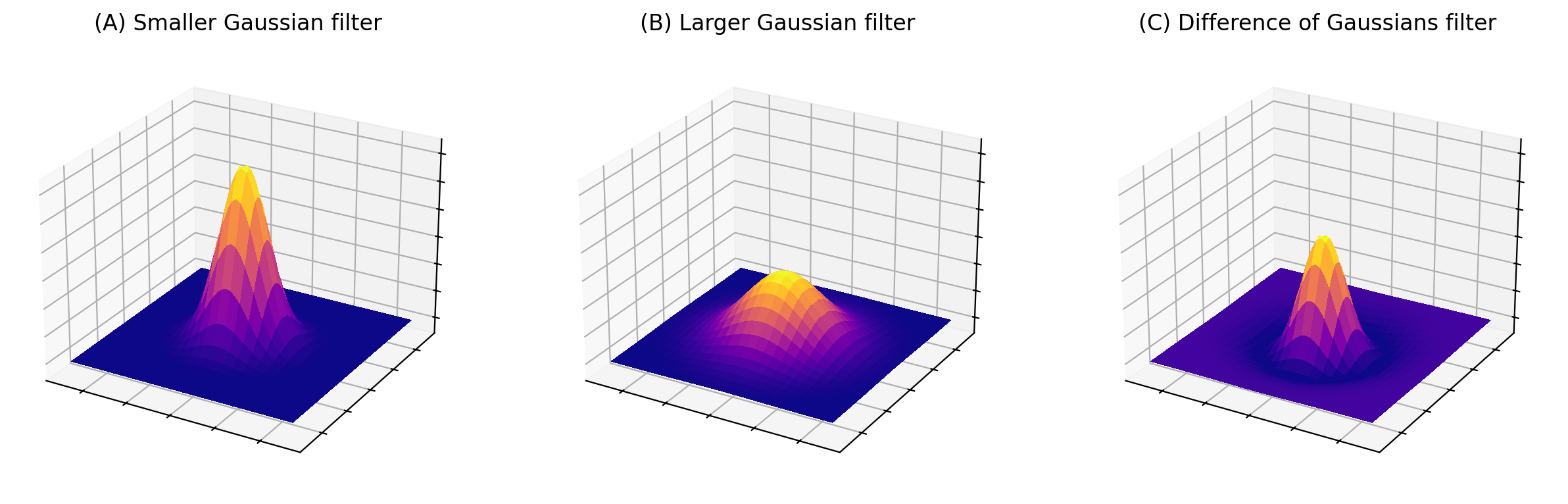
Figura 96 Gráficos de superficie de dos filtros Gaussianos con \(\sigma\) pequeño y grande, y el resultado de restar el último del primero. La suma de los coeficientes de (A) y (B) es uno en cada caso, mientras que los coeficientes de (C) suman cero.

Laplaciano de filtrado Gaussiano

Una complicación menor con el filtrado DoG es la necesidad de seleccionar dos valores diferentes de \(\sigma\). Una operación similar, que requiere solo un único \(\sigma\) y un solo filtro, es el filtrado Laplaciano de Gaussiano (LoG).

La apariencia de un filtro LoG es como un filtro DoG al revés (Figura 97), pero si la imagen resultante está invertida, entonces los resultados son comparables [^fn_4].

Show code cell content Hide code cell content

fig = create_figure(figsize=(8, 4))

def log_kernel(shape, sigma: float):
    """
    Create an image with a single 1 in the middle,
    the apply a Gaussian filter to get the coefficients.
    """
    filt = np.zeros(shape)
    filt[shape[0]//2, shape[1]//2] = 1.0
    return ndimage.gaussian_laplace(filt, sigma)

n = 25
x = np.arange(-n, n+1, 1)
y = np.arange(-n, n+1, 1)
x, y = np.meshgrid(x, y)
sigma = 6

#
z_log = ((x*x + y*y - 2 * sigma*sigma)/(np.power(sigma, 4))) * np.exp(-(x*x + y*y)/(2 * sigma * sigma))

fig, ax = plt.subplots(1, 2, subplot_kw=dict(projection='3d', elev=25), figsize=(10, 5))
ax[0].plot_surface(x, y, z_log, **surf_args)
ax[1].plot_surface(x, y, -z_log, **surf_args)
for a in ax:
    a.set_xticklabels([])
    a.set_yticklabels([])
    a.set_zticklabels([])

ax[0].set_title('LoG filter')
ax[1].set_title('Inverted LoG filter')

glue_fig('fig_log_plots', fig)

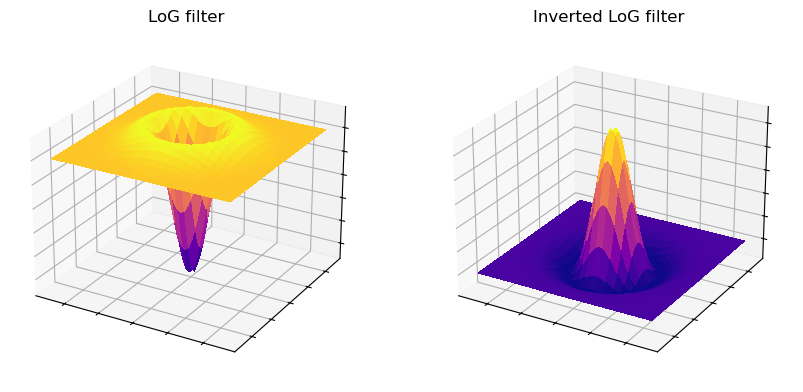
Figura 97 Gráfico de superficie de un filtro LoG. Esto se parece mucho a Figura 96, pero invertido para que los valores negativos se encuentren en el centro del filtro.

Show code cell content Hide code cell content

fig = create_figure(figsize=(8, 4))

im = load_image('images/dog_on_log_orig.png').astype(np.float32)

show_image(im, title="(A) Dog on a log", pos=131)

sigma_dog = 2
im_dog = ndimage.gaussian_filter(im, sigma_dog) - ndimage.gaussian_filter(im, sigma_dog * 1.6)
show_image(im_dog, title="(B) DoG filtered dog", clip_percentile=0.25, pos=132)

sigma_log = 2
im_log = ndimage.gaussian_laplace(im, sigma_log)
show_image(im_log, title="(C) LoG filtered dog", clip_percentile=0.25, pos=133)

glue_fig('fig_dog_on_log', fig)

Figura 98 Aplicación de filtrado DoG y LoG a una imagen. Ambos métodos mejoran la apariencia de estructuras tipo manchas y (en menor medida) de los bordes, y dan como resultado una imagen que contiene valores positivos y negativos con una media general de cero. En el caso del filtrado LoG, se produce una inversión: los puntos más oscuros se vuelven brillantes después del filtrado.

Enmascaramiento de desenfoque

Finalmente, una técnica relacionada ampliamente utilizada para mejorar la visibilidad de los detalles en las imágenes (aunque ciertamente no aconsejable para el análisis cuantitativo) es el enmascaramiento de desenfoque.

Esto utiliza un filtro Gaussiano primero para difuminar los bordes de una imagen y luego los resta del original. Pero en lugar de detenerse allí, la imagen restada se multiplica por algún factor de ponderación y se vuelve a agregar al original. Esto da una imagen que se parece mucho a la original, pero con bordes afilados en una cantidad que depende del peso elegido.

Show code cell content Hide code cell content

fig = create_figure(figsize=(8, 4))

im = load_image('images/unsharp_masking_orig.png').astype(np.float32) / 255
if im.ndim > 2:
    im = im[:, :, 0]

show_image(im, title="(A) Original image", pos=131)

sigma = 8
im_gauss = ndimage.gaussian_filter(im, sigma)
im_diff = im - im_gauss
show_image(im_diff, title="(B) Gaussian subtracted", clip_percentile=0.25, pos=132)

im_unsharp = im + im_diff * 2
im_unsharp = np.clip(im_unsharp, 0, 1)
show_image(im_unsharp, title="(C) Unsharp masked", pos=133)

glue_fig('fig_unsharp_masking', fig)

Figura 99 La aplicación de máscara de desenfoque a una imagen borrosa. Primero, se resta una versión suavizada Gaussiana de la imagen (\(\sigma = 1\)) del original, se escala (\(peso = 0,7\)) y se vuelve a agregar al original.

El enmascaramiento de desenfoque puede mejorar la apariencia visual de una imagen, pero es importante recordar que modifica el contenido de la imagen de una manera que bien podría considerarse sospechosa en los círculos científicos. Por lo tanto, si aplicas una máscara de desenfoque a cualquier imagen que desees compartir con el mundo, debes tener una buena justificación y ciertamente admitir lo que has hecho. La técnica se incluye aquí no como una recomendación para su uso, sino más bien para mostrar cómo se pueden combinar los filtros Gaussianos con operaciones puntuales de manera creativa.

Si deseas un método más justificado teóricamente para mejorar la nitidez de la imagen en microscopía, puede que valga la pena investigar los algoritmos de “(máxima probabilidad) deconvolución”.

---

[1]

Me siento obligado a admitir que hay una sutil diferencia entre convolución y correlación: el núcleo (kernel) se gira 180° para la convolución. Esto es algo de lo que casi nunca debemos preocuparnos por dos razones:

1. La convolución y la correlación terminan igual si el filtro es simétrico, y la mayoría de los filtros que nos interesan son simétricos.

2. De todos modos, la distinción a menudo se ignora en la práctica. Por ejemplo, ImageJ tiene un comando Process ‣ Filters ‣ Convolve… que (la última vez que verifiqué) en realidad implementa la correlación.

[2]

La ecuación entonces se parece al teorema de Pitágoras: \(G_{mag} = \sqrt{G_x^2 + G_y^2}\)

[3]

Un filtro LoG también suele denominarse filtro de sombrero mexicano, aunque claramente el filtro (o el usuario del sombrero) debe invertirse para que el nombre tenga más sentido.