Desenfoque y Función de dispersión de punto (Point Spread Function o PSF por sus siglas en inglés)#
Outline del capítulo
Las mediciones en microscopía de fluorescencia se ven afectadas por el desenfoque.
El desenfoque actúa como una convolución con la Función de dispersión de punto (PSF) del microscopio.
El tamaño de la PSF depende del tipo de microscopio, de la longitud de onda de la luz y de la apertura numérica (NA) del objetivo, y es del orden de cientos de nm.
En el plano focal, la PSF es un patrón de aire.
La resolución espacial es una medida de lo cerca que pueden distinguirse las estructuras. Es mejor en xy que a lo largo de la dimensión z.
Show code cell content
%load_ext autoreload
%autoreload 2
# Default imports
import sys
sys.path.append('../../../')
from helpers import *
from matplotlib import pyplot as plt
from myst_nb import glue
import numpy as np
from scipy import ndimage
Introducción#
Las imágenes de microscopía suelen verse borrosas porque la luz que se origina en un punto de la muestra no se detecta toda en un único píxel: normalmente se detecta en varios píxeles y cortes z. Esto no se debe simplemente a que no podamos utilizar lentes perfectas, sino a un límite fundamental impuesto por la naturaleza de la luz. El resultado final es como si la luz que detectamos se redistribuyera ligeramente a través de nuestros datos (Figura 133).
Show code cell content
fig = create_figure(figsize=(8, 4))
show_image('images/castle_sharp.jpg', title='(A) Sharp', pos=121)
show_image('images/castle_convolved.jpg', title='(B) Blurred', pos=122)
glue_fig('fig_blur_castles', fig)

Figura 133 Diagrama esquemático que muestra los efectos del desenfoque. Piense en la arena como fotones, y en la altura del castillo de arena como los valores de intensidad de los píxeles (una mayor altura indica más fotones y, por tanto, un píxel más brillante). Los datos ideales serían nítidos y podrían contener detalles finos (A), pero tras el desenfoque no sólo es más difícil discriminar los detalles, sino que las intensidades en las regiones más brillantes se han reducido y los tamaños han aumentado (B). Si luego queremos determinar el tamaño o la altura de una de las torres del castillo de arena, por ejemplo, debemos recordar que los resultados que obtengamos midiendo (B) diferirán de los que habríamos obtenido si hubiéramos podido medir la propia (A). Sin embargo, hay que tener en cuenta que en ambos casos hay aproximadamente la misma cantidad de señal (arena o fotones), sólo ha cambiado la distribución.#
Esto es importante por tres razones:
El desenfoque afecta al tamaño aparente de las estructuras
El desenfoque afecta a la intensidad aparente (es decir, al brillo) de las estructuras
El desenfoque (a veces) afecta al número aparente de estructuras
Por lo tanto, casi todas las mediciones que queramos hacer pueden verse afectadas por el desenfoque hasta cierto punto.
Ésa es la mala noticia sobre el desenfoque. La buena noticia es que se entiende bastante bien, y podemos tranquilizarnos sabiendo que no es aleatorio. De hecho, las ideas principales ya se han descrito en Filtros, porque el desenfoque en microscopía de fluorescencia se describe matemáticamente mediante una convolución en la que interviene la Función de dispersión puntual (PSF) del microscopio. En otras palabras, la PSF actúa como un filtro lineal aplicado a los datos perfectos y nítidos que desearíamos, pero que nunca podemos adquirir directamente.
Anteriormente, vimos cómo los filtros de suavizado (por ejemplo, medio o gaussiano) podían ayudar a reducir el ruido, pero a medida que aumentaba el tamaño del filtro perdíamos cada vez más detalle. En ese punto, podíamos elegir nosotros mismos el tamaño y la forma de los filtros, cambiándolos arbitrariamente al modificar los coeficientes para conseguir el equilibrio entre reducción de ruido y pérdida de detalle que más nos gustara. Pero el desenfoque del microscopio difiere en al menos dos aspectos importantes. En primer lugar, se aplica a nuestros datos antes de que intervenga el ruido, por lo que no ofrece ventajas en cuanto a la reducción del ruido. En segundo lugar, como se produce antes de que pongamos los ojos en nuestras imágenes, el tamaño y la forma del filtro utilizado (es decir, la PSF) sólo están indirectamente (y de forma muy limitada) bajo nuestro control. Por lo tanto, sería mucho mejor prescindir por completo del desenfoque, ya que no ofrece ninguna ayuda real, pero por desgracia la luz conspira para que esto no sea una opción: simplemente tenemos que lidiar con ello.
El propósito de este capítulo es ofrecer una introducción práctica a por qué se produce el desenfoque, qué aspecto tiene la PSF de un microscopio de campo amplio y por qué todo esto es importante. No se incluyen ópticas detalladas ni integrales amenazadoras, aunque aparecen varias ecuaciones. Afortunadamente para los poco entusiastas de las matemáticas, éstas son breves y útiles.
Desenfoque y convolución#
Como ya se ha dicho, la causa fundamental del desenfoque es que la luz que se origina desde un punto infinitesimalmente pequeño no puede detectarse en un punto similar, por muy grandes que sean nuestras lentes o detectores. En lugar de ello, acaba siendo enfocada hacia un volumen mayor, conocido como PSF, que tiene un tamaño mínimo que depende tanto de la longitud de onda de la luz como de la lente utilizada.
Show code cell content
fig = create_figure(figsize=(8, 4))
show_image('images/psf_sizes_orig.png', title='(A) Entire image', pos=141)
show_image('images/psf_sizes_detail.png', title='(B) Detail of (A)', pos=142)
show_image('images/psf_sizes_small.png', title='(C) Some blur', pos=143)
show_image('images/psf_sizes_large.png', title='(D) A lot of blur', pos=144)
glue_fig('fig_blur_psf_sizes', fig)

Figura 134 Aunque no resulte obvio a bajo aumento (A), una imagen puede verse como compuesta de pequeños puntos (B). Esto nos proporciona una forma útil de entender lo que ha sucedido en una imagen borrosa: cada punto ha sido simplemente sustituido por una mancha más difusa, la PSF. Las imágenes aparecen más o menos borrosas en función del tamaño de las manchas PSF (C) y (D). Esto equivale a aplicar la PSF a una imagen como un filtro lineal.#
Esto adquiere mayor relevancia práctica si tenemos en cuenta que cualquier muestra fluorescente puede verse como compuesta de muchos puntos emisores de luz similares y extremadamente pequeños (se puede pensar que cada punto es un fluoróforo). Lo ideal sería que nuestra imagen incluyera también puntos individuales, digitalizados en píxeles con valores proporcionales a la luz emitida. Pero lo que obtenemos en su lugar es una imagen en la que cada punto ha sido sustituido por su PSF, escalada según el brillo del punto. Cuando estas PSF se superponen, las intensidades de luz detectadas simplemente se suman. La borrosidad de la imagen depende del tamaño de la PSF (Figura 134).
Este proceso de desenfoque es equivalente a convolucionar la (imposible) imagen ideal de puntos, con la PSF: es decir, aplicar un filtro lineal, como se describe en Filtros. Dado que todos los puntos se desenfocan de la misma manera (al menos en el caso ideal; las aberraciones adicionales pueden causar algunas variaciones), esto significa que si conocemos la PSF podemos caracterizar el desenfoque en toda la imagen y, por tanto, hacer inferencias sobre el grado en que el desenfoque afectará cualquier cosa que midamos.
La forma de la PSF#
Podemos obtener una primera impresión de la PSF de un microscopio registrando una serie de planos z (z-stack) de una pequeña perla fluorescente, que representa un punto ideal de emisión de luz. Figura 135 muestra que, para un microscopio de campo amplio, la perla aparece como una mancha brillante cuando está enfocada. Y lo que es más curioso, cuando se mira desde un lado (xz o yz), tiene un aspecto similar al de un reloj de arena, aunque con algunos patrones adicionales. Esta forma exacta se conoce lo suficientemente bien como para que las PSF también puedan generarse teóricamente basándose en el tipo de microscopio y lentes objetivo utilizados (C).
Show code cell content
fig = create_figure(figsize=(8, 4))
show_image('images/bead_linear.png', title='(A) Bead (linear)', pos=131)
show_image('images/bead_gamma.png', title='(B) Bead (gamma))', pos=132)
show_image('images/bead_theoretical.png', title='(C) Theoretical PSF (linear)', pos=133)
glue_fig('fig_blur_psf_bead', fig)
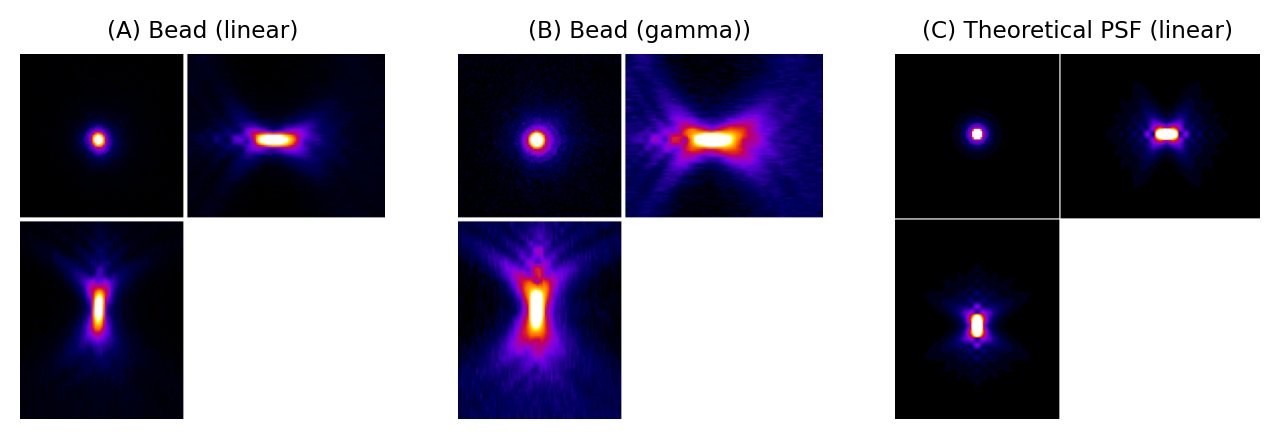
Figura 135 La PSF de un microscopio de campo amplio. (A) y (B) son series de plano z (z-stacks) adquiridas de una pequeña perla fluorescente, mostradas usando contraste lineal y tras aplicar una transformación gamma para hacer que los detalles más débiles sean más fáciles de discernir (ver Operaciones puntuales para más información). (C) muestra una PSF teórica para un microscopio similar. Su aspecto difiere en parte porque la perla no es realmente un punto infinitamente pequeño, y en parte porque la lente objetivo del microscopio real no es perfecta. No obstante, las formas generales son similares.#
Generación de PSF
Los plugins de ImageJ para crear PSF teóricas están disponibles en
Enfoque y desenfoque#
Figura 136 intenta mostrar que el aspecto de reloj de arena de la PSF es en realidad perfectamente intuitivo. Al grabar una serie de plano z (z-stacks) de un punto emisor de luz, preferiríamos que la luz acabara en un único píxel de un único corte. Pero la propia luz es ajena a nuestros deseos, y fácilmente se detectará si golpea un detector, sin importar dónde se encuentre. Por lo tanto, lo que debemos esperar es que la luz se detectará en una pequeña región sólo si la imagen está enfocada; de lo contrario, se dispersará en una medida que dependerá de la distancia a la que se detecte del punto focal. Desde el lado (xz o yz), esto da lugar a una forma de reloj de arena.

Figura 136 Diagrama simplificado para ayudar a visualizar cómo se obtendría una imagen de un punto emisor de luz utilizando un microscopio de campo amplio. Parte de la luz procedente del punto es captada por una lente. Si se imagina que la luz se dirige hacia un punto focal, se obtiene la forma de un reloj de arena. Si se coloca un detector cerca del punto focal, la imagen en forma de punto formada por la luz que incide en el detector sería pequeña y brillante. Sin embargo, si el detector se situara por encima o por debajo de este plano focal, la intensidad del punto disminuiría y su tamaño aumentaría.#
Enfocado, un punto emisor de luz parece una pequeña mancha brillante. Desenfocado, es mucho menos brillante y se extiende por una zona más amplia.
Sin embargo, ¿cómo esperaría que la cantidad total de luz difiriera en una imagen de campo amplio dependiendo de si un plano está enfocado o no? En otras palabras, ¿esperaría más o menos luz en el plano focal que en otros planos situados por encima o por debajo de él?
En una imagen de campo amplio, cada plano que podemos registrar contiene luz enfocada junto con toda la luz detectable de todos los demás planos sumados. Por tanto, deberíamos esperar aproximadamente la misma cantidad total de luz dentro de cada plano de una serie de plano z (z-stack), sólo que distribuida de forma diferente. Eso potencialmente es mucha luz en el lugar «equivocado», especialmente si se observa una muestra gruesa.
Al menos, esto sería así para un detector infinitamente grande, o una muestra pequeña y centrada. En la práctica, si la luz se origina en un lugar tan desenfocado que su luz se derrama por el lado del detector, entonces este plano contendría menos luz.
La aparición de interferencias#
Figura 136 es bastante limitado en lo que muestra: no empieza a explicar los patrones adicionales de la PSF, que aparecen en cada plano 2D como anillos concéntricos (véase Figura 137) ni por qué la PSF no se reduce a un único punto en el plano focal. Estos factores están relacionados con la interferencia de las ondas luminosas. Aunque es importante saber que existen anillos, aunque sólo sea para evitar malinterpretarlos como estructuras anulares adicionales realmente presentes en una muestra, su influencia en cualquier análisis es limitada, ya que la región central de la PSF es abrumadoramente más brillante. Por lo tanto, para nuestros propósitos, pueden ignorarse en su mayor parte.
Show code cell content
fig = create_figure(figsize=(8, 6))
for ii in range(10):
show_image(f'images/bead_slices_{ii}.png', pos=(2, 5, ii+1))
glue_fig('fig_blur_bead_slices', fig)
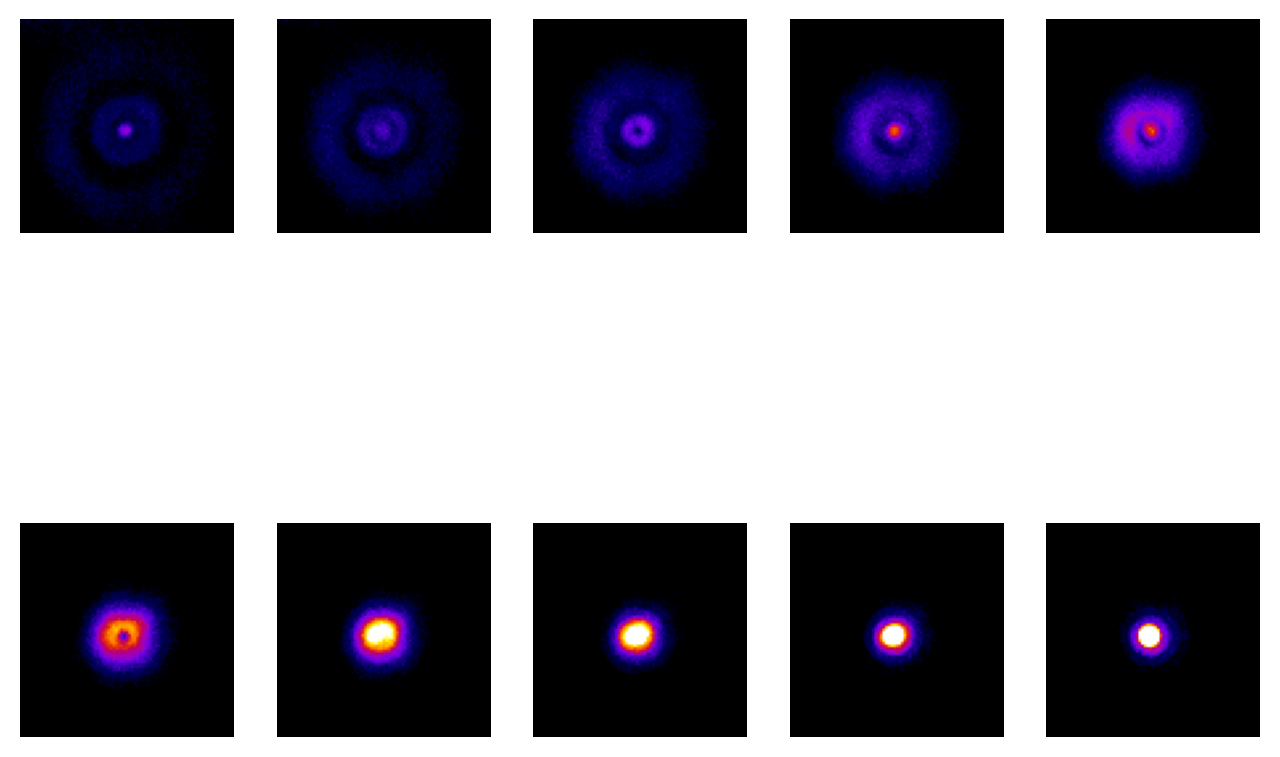
Figura 137 Diez cortes de una serie de plano z (z-stack) adquirida de una perla fluorescente, empezando desde arriba y bajando hasta el plano focal. Se han aplicado los mismos ajustes de contraste lineal a cada corte para facilitar la comparación, aunque esto hace que la perla enfocada aparezca saturada, ya que de lo contrario los anillos no serían visibles en absoluto. Dado que la imagen es (aproximadamente) simétrica a lo largo del eje z, los cortes adicionales que se desplacen por debajo del plano focal tendrían un aspecto similar.#
El disco Airy#
Por último, para esta sección, la PSF en el plano focal es lo suficientemente importante como para merecer algo de atención, ya que tendemos a querer medir las cosas donde están más enfocadas. Todo este plano xy, incluidas sus ondulaciones interferentes, se denomina patrón de Airy, mientras que la parte central brillante por sí sola es el disco de Airy (Figura 138). En el mejor de los casos, cuando toda la luz de una imagen 2D procede de estructuras enfocadas, lo que podemos ver ya se habría hecho borroso por un filtro con este aspecto.
Show code cell content
def demo_airy_disk(radius=10, size=128):
"""
Create an Airy disk image for illustration.
Parameters:
radius: radius of the Airy disk, in pixels
size: width and height of the image, in pixels
"""
from scipy.special import j1
s = 3.83 / radius
x = np.arange(size, dtype=np.float64) * s
x -= x.mean()
y, x = np.meshgrid(x, x)
r = np.sqrt(x*x + y*y)
result = np.ones(r.shape)
result[r != 0] = (2 * j1(r[r != 0]) / r[r != 0])**2
return result, y, x
from matplotlib import colormaps
cmap = colormaps['inferno']
im_airy, y, x = demo_airy_disk(radius = 10, size = 65)
fig = create_figure(figsize=(8, 2.5))
# ax_cartoon = fig.add_subplot(1, 3, 1)
# ax_disk = fig.add_subplot(1, 3, 2)
# ax_3d = fig.add_subplot(1, 3, 3, projection='3d', elev=20)
show_image('images/Airy.jpg', title='(A) George Biddell Airy (1801–1892)', pos=131)
show_image(im_airy, title='(B) Airy pattern', vmin=-0.05, vmax=0.8, cmap=cmap, pos=132)
show_image(im_airy, title='(C) Airy pattern (contrast enhanced)', vmin=-0.05, vmax=0.1, cmap=cmap, pos=133)
plt.tight_layout()
glue_fig('fig_blur_airy', fig)
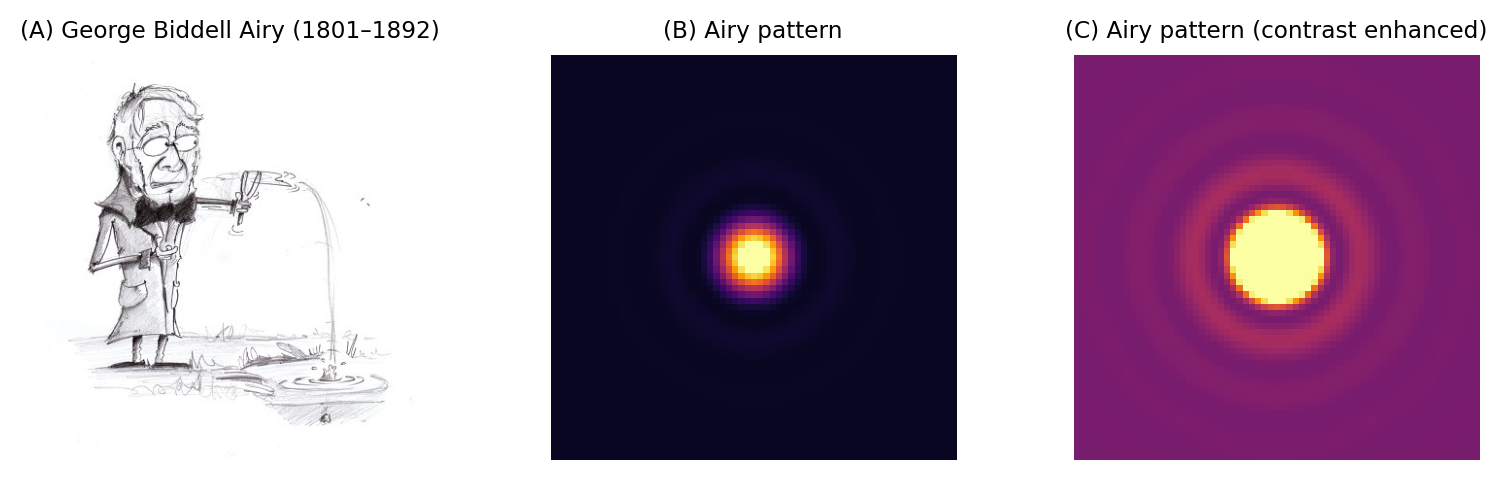
Figura 138 George Biddell Airy y el patrón de Airy. (A) En sus tiempos de estudiante, Airy era conocido por su destreza «en la construcción de tiradores de guisantes y otros artefactos similares» (véase https://mathshistory.st-andrews.ac.uk/Biographies/Airy/). Los anillos que rodean el disco de Airy se han comparado con las ondas de un estanque. Aunque el fenómeno de los anillos ya era conocido, Airy escribió el primer tratamiento teórico del mismo en 1835 (https://en.wikipedia.org/wiki/Airy_disk). (B) Un patrón de Airy se parece mucho a una función gaussiana 2D, aunque cuando se aumenta el contraste (C) pueden verse pequeños anillos exteriores rodeando el disco de Airy.#
El disco de Airy debería resultarnos familiar. Si ignoramos las pequeñas ondulaciones que interfieren en sus bordes, nos podemos aproximar muy bien mediante una función gaussiana (Figura 139). Por tanto, el desenfoque de un microscopio en 2D es similar a aplicar un filtro gaussiano, al menos en el plano focal.
Show code cell content
"""
Show 3D plots to compare an Airy disk with a 2D Gaussian function.
"""
# Create an Airy disk image
radius = 10
im_airy, y, x = demo_airy_disk(radius=radius, size = 65)
# Compute FWHM from the Airy disk radius,
# convert to a Gaussian sigma & then create 2D Gaussian
fwhm = radius / 3.232
sigma = fwhm / (2 * np.sqrt(2 * np.log(2)))
im_gaussian = np.exp(-(x*x + y*y)/(2 * sigma * sigma))
# Show plots
color_airy = '#1f77b4'
color_gaussian = '#ff7f0e'
fig = create_figure(figsize=(8, 2.5))
ax_disk = fig.add_subplot(1, 3, 1, projection='3d', elev=20)
ax_gaussian = fig.add_subplot(1, 3, 2, projection='3d', elev=20)
ax_fit = fig.add_subplot(1, 3, 3)
ax_disk.plot_wireframe(x, y, im_airy, color=color_airy, linewidth=0.5)
ax_gaussian.plot_wireframe(x, y, im_gaussian, color=color_gaussian, linewidth=0.5)
row = im_airy.shape[0]//2
show_plot(y[row, :], im_airy[row, :], color=color_airy, axes=ax_fit)
show_plot(y[row, :], im_gaussian[row, :], color=color_gaussian, axes=ax_fit)
titles = ['(A) Airy disk',
'(B) Gaussian function',
'(C) Gaussian fit to Airy disk']
for ax, title in zip([ax_disk, ax_gaussian, ax_fit], titles):
ax.set_title(title, fontdict={'fontsize':'small'})
ax.set_xticklabels([])
ax.set_yticklabels([])
try:
ax.set_zticklabels([])
except:
pass
glue_fig('fig_blur_psf_surface', fig)
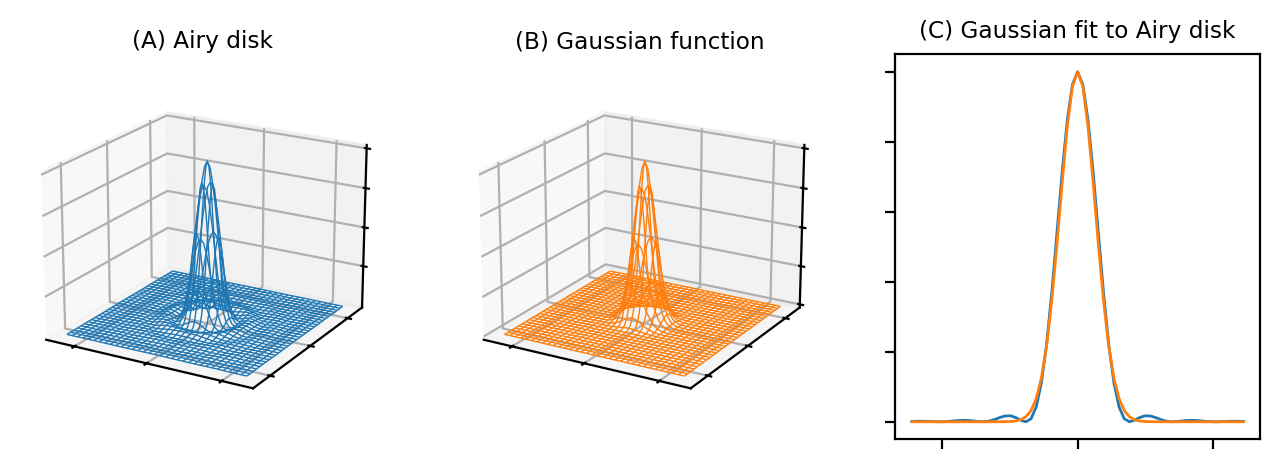
Figura 139 Comparación de un disco de Airy y una gaussiana de tamaño similar, utilizando dos gráficos de alambre y la sección transversal 1D correspondiente. La gaussiana es muy parecida al disco de Airy, aparte de las débiles ondulaciones laterales, por lo que a menudo podemos aproximar el desenfoque de una PSF utilizando un filtro gaussiano.#
El tamaño de la PSF#
Menos mal que las apariencias no nos engañan. Para juzgar cómo afectará el desenfoque a lo que podemos ver y medir, necesitamos saber el tamaño de la PSF. Como usualmente no queremos que nuestras imágenes salgan borrosas, es preferible que sean más pequeñas.
El tamaño requiere cierta definición: en realidad, la PSF continúa indefinidamente, pero tiene valores de intensidad extremadamente bajos cuando se aleja de su centro. Un método para caracterizar el tamaño del disco de Airy es considerar su radio \(r_{airy}\) como la distancia desde el centro hasta el primer mínimo: el punto más bajo antes de que comience la primera de las ondulaciones exteriores. Esto viene dado por:
donde \(\lambda\) es la longitud de onda de la luz y NA es la apertura numérica de la lente objetivo [^fn_1].
Una medida comparable a \(r_{airy}\) entre el centro y el primer mínimo a lo largo del eje z es:
donde \(\eta\) es el índice de refracción del medio de inmersión de la lente objetivo (que es un valor relacionado con la velocidad de la luz a través de ese medio).
La importancia práctica de estas ecuaciones es que revelan los factores clave que influyen en el grado de desenfoque de una imagen. De este modo, es posible reducir el desenfoque durante la etapa de adquisición de imagen.
Según la ecuación (1), la ecuación para el tamaño del disco de Airy, ¿cuáles son las dos variables que podríamos controlar y que influyen en la cantidad de desenfoque de nuestras imágenes? ¿Y cómo hay que cambiarlas (aumentarlas o disminuirlas) para que las imágenes tengan menos desenfoque?
Si la longitud de onda \(\lambda\) es más baja o el objetivo NA es más alto, \(r_{airy}\) disminuye y tenemos menos desenfoque.
¿Influye más la NA en el desenfoque en el plano xy, o a lo largo del eje z?
Debido a la elevación al cuadrado, la NA tiene una influencia mucho mayor en el desenfoque a lo largo del eje z que en xy. Esto puede verse claramente en Figura 140.
Show code cell content
fig = create_figure(figsize=(8, 4))
show_image('images/psf_na_names.png', pos=141)
show_image('images/psf_na_08.png', title='NA = 0.8', pos=142)
show_image('images/psf_na_1.png', title='NA = 1.0', pos=143)
show_image('images/psf_na_12.png', title='NA = 1.2', pos=144)
glue_fig('fig_blur_psf_na', fig)
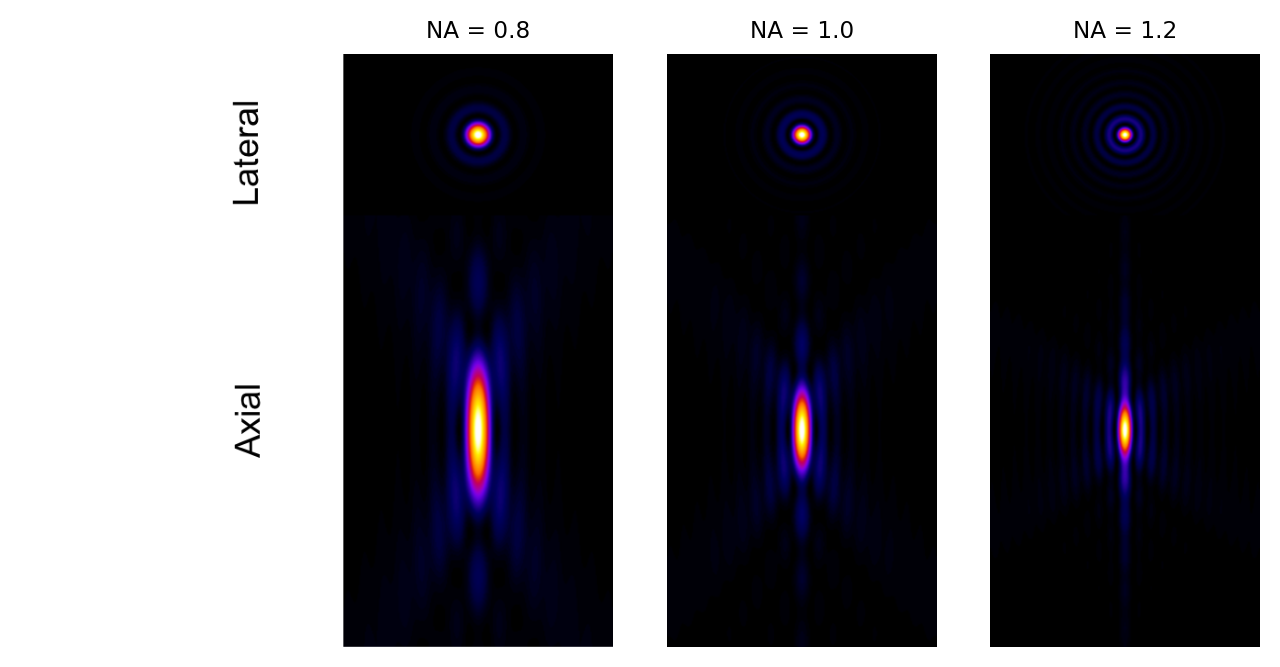
Figura 140 Ejemplos de PSF teóricas generadas con diferentes aperturas numéricas.#
Apertura numérica (NA por sus siglas en inglés)
Las ecuaciones para el tamaño del PSF muestran que si se puede utilizar una lente objetivo con una NA más alta, se puede reducir potencialmente el desenfoque en una imagen – especialmente a lo largo del eje z (Figura 140). Por desgracia, pronto se llega a otro límite en cuanto a lo que se puede conseguir aumentando la NA. Esto se puede ver en la ecuación utilizada para definirlo:
donde \(\eta\) es de nuevo el índice de refracción del medio de inmersión y \(\theta\) es el semiángulo del cono de luz aceptado por el objetivo. Dado que \(\sin{\theta}\) nunca puede superar 1, el NA nunca puede superar \(\eta\), que a su vez tiene valores fijos (por ejemplo, alrededor de 1,0 para el aire, 1,34 para el agua o 1,5 para el aceite). Por lo tanto, los objetivos con una NA elevada sólo pueden reducir el desenfoque de forma limitada.
Una consideración adicional importante es que las mayores NA son posibles cuando el índice de refracción de la inmersión es alto, pero si éste no coincide con el índice de refracción del medio que rodea la muestra, obtenemos una aberración esférica. Esto se trata de un fenómeno por el cual la PSF se vuelve asimétrica conforme aumenta la profundidad y el desenfoque se vuelve más extraño. Por lo tanto, a menudo es preferible que los índices de refracción de los medios de inmersión e incrustación coincidan, a que se utilice el objetivo de mayor NA disponible: normalmente es mejor tener una PSF más grande que una muy irregular.
Para ver un tutorial interactivo sobre el efecto del uso de diferentes NA, consulte https://www.microscopyu.com/tutorials/imageformation-airyna.
Convénzase por si mismo de que \(z_{min}\) será considerablemente mayor que \(r_{airy}\) utilizando uno de los siguientes métodos:
Ponga un índice de refracción de ejemplo (por ejemplo, \(\eta = 1,34\) para el agua), y algunos valores razonables de \(\lambda\) y la NA en las ecuaciones para la resolución lateral (1) y axial (2), y compare los resultados
Calcule la relación \(z_{min} / r_{airy}\) y sustitúyala en la ecuación de la NA. Esto debería revelar que la relación es mayor que 1, es decir, que \(z_{min}\) es mayor.
¿Cuál es la principal implicación de esta observación, en términos de cuán separadas deben estar las estructuras a lo largo de diferentes dimensiones para que sigan siendo distinguibles?
La relación es
Por lo tanto, incluso cuando \(\sin\theta\) se acerca a 1 (es decir, se utiliza un objetivo de NA muy alto), el valor de \(z_{min}\) sigue siendo más de 3 veces mayor que \(r_{airy}\) – la resolución z es mucho peor. Cuando la NA es menor, la diferencia es aún mayor.
La principal implicación práctica es que es más probable que pueda distinguir estructuras separadas entre sí por una corta distancia en xy que separadas de forma similar en z. Si realmente necesita información en la dimensión z más que en cualquier otra parte, ¿quizá la rotación de la muestra pueda ayudarle?
Resolución espacial#
La resolución espacial se refiere a la distancia que puede haber entre dos estructuras sin que dejen de distinguirse. Se trata de una idea un tanto subjetiva y difusa, pero una forma de definirla es mediante el Criterio Rayleigh, según el cual se dice que dos manchas igualmente brillantes están resueltas (es decir, son distinguibles) si están separadas por las distancias calculadas en las ecuaciones anteriores (1) y (2). Si las manchas están más cerca, es probable que se vean como una sola. En el plano de enfoque, esto se ilustra en Figura 141.
Show code cell content
def shift_horizontal(im, n: int):
"""
Shift an image horizonally left or right, padding with zeros.
"""
if n == 0:
return im
if n > 0:
return np.pad(im[:, :-n], pad_width=((0, 0), (n, 0)))
else:
return np.pad(im[:, -n:], pad_width=((0, 0), (0, -n)))
# Create an Airy disk in a (reasonably) big image
radius = 40
pad = 2
im_airy, x, y = demo_airy_disk(radius=radius, size=radius*pad*2+1)
x = np.arange(-radius*pad, radius*pad+1) / radius
row = im_airy.shape[0]//2
im_airy_2 = shift_horizontal(im_airy, -radius) + shift_horizontal(im_airy, radius)
im_airy_1 = shift_horizontal(im_airy, -radius//2) + shift_horizontal(im_airy, radius//2)
im_airy_0_8 = shift_horizontal(im_airy, -int(radius*0.4)) + shift_horizontal(im_airy, int(radius*0.4))
im_airy_0_5 = shift_horizontal(im_airy, -int(radius*0.25)) + shift_horizontal(im_airy, int(radius*0.25))
# Show plots
fig = create_figure(figsize=(8, 4))
img_args = dict(
cmap=colormaps['magma'],
vmin=0,
vmax=1
)
show_image(im_airy_2, title='(A) 2 radii separation', **img_args, pos=241)
show_image(im_airy_1, title='(B) 1 radius separation', **img_args, pos=242)
show_image(im_airy_0_8, title='(C) 0.8 disk separation', **img_args, pos=243)
show_image(im_airy_0_5, title='(D) 0.5 disk separation', **img_args, pos=244)
plot_args = dict(
ylim=[-0.1, 1.8],
xlabel='Disk radii'
)
show_plot(x, im_airy_2[row, :], **plot_args, pos=245)
show_plot(x, im_airy_1[row, :], **plot_args, pos=246)
plt.yticks([])
show_plot(x, im_airy_0_8[row, :], **plot_args, pos=247)
plt.yticks([])
show_plot(x, im_airy_0_5[row, :], **plot_args, pos=248)
plt.yticks([])
glue_fig('fig_blur_rayleigh', fig)
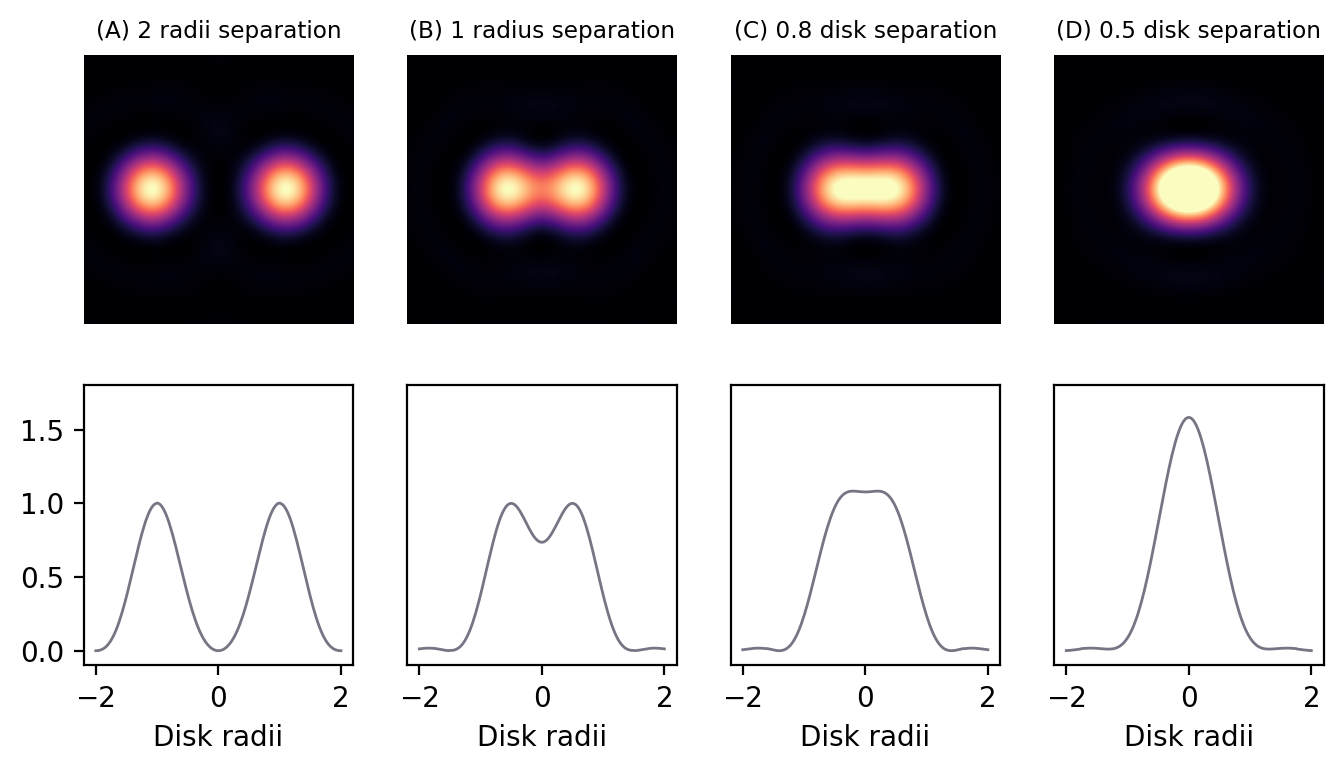
Figura 141 Patrones de Airy separados por diferentes distancias, definidas en términos de radios de disco de Airy. La fila superior contiene los patrones mismos, mientras que la fila inferior muestra los perfiles de intensidad calculados a través de los centros de los patrones. Se aprecian claramente dos manchas que son claramente visibles siempre que estén separadas por al menos un radio de disco, y que el perfil muestre una caída. Sin embargo, si la separación es inferior a un radio, el contraste rápidamente disminuye hasta que sólo se aprecia una sola estructura. Con una separación de 0,5 radios, las dos estructuras parecen indistinguibles como una única estructura más brillante.#
Hay que tener en cuenta que el uso de \(r_{airy}\) y \(z_{min}\) en el criterio de Rayleigh es un tanto arbitrario, y los efectos de las diferencias de brillo, el tamaño finito de los píxeles y el ruido complican aún más la situación, de modo que en la práctica puede ser necesaria una distancia mayor para que podamos distinguir con seguridad las estructuras. No obstante, el criterio de Rayleigh es útil para dar una idea de la escala de las distancias implicadas, por ejemplo cientos de nanómetros cuando se utiliza luz visible.
Supongamos que el diámetro del disco de Airy es alrededor de 500 nm y que usted está observando una imagen que contiene estructuras separadas y bien espaciadas de 2 nm, 20 nm y 200 nm de tamaño. Suponiendo que las haya enfocado todas exactamente (después de todo, usted es un microscopista brillante), ¿cómo aparecerán estas estructuras en la imagen?
Nota:_ ¡Ésta es una pregunta especialmente importante! Piense tanto en el tamaño como en la luminosidad.
Dado que ni siquiera un punto infinitesimal puede parecer más pequeño que el disco de Airy en la imagen grabada, es posible que las tres estructuras tengan el mismo aspecto. Puede que se aprecie un cierto aumento de tamaño en la estructura de 200 nm (dado que es mayor que un único punto, se asemeja a la suma de varios discos de Airy en su mayoría superpuestos pero con un ligero desplazamiento), pero desde luego no parecerá 10 o 100 veces mayor que las otras estructuras.
Sin embargo, como los objetos más pequeños suelen emitir menos fotones, las estructuras más pequeñas pueden parecer menos brillantes, si es que lo suficientemente brillantes como para ser visibles. Por lo tanto, a esta escala es imposible realizar mediciones precisas del tamaño a partir de imágenes de microscopía de fluorescencia convencional (sin super-resolución). Sin embargo, el tamaño real puede guardar cierta relación con el brillo.
Medición de PSF y estructuras pequeñas#
Saber que el disco de Airy se parece a una función gaussiana es extremadamente útil, porque cada vez que vemos un disco de Airy podemos ajustarle una gaussiana 2D. Los parámetros de la función nos dirán con exactitud el centro de la gaussiana, que corresponde al lugar donde se encuentra realmente la estructura fluorescente, aunque no con total precisión, pero potencialmente más allá de la precisión incluso del tamaño del píxel (el ruido es la verdadera limitación). Esta idea es fundamental para las técnicas de localización de moléculas individuales, incluidas las de los microscopios de super-resolución como STORM y PALM, pero requiere que las PSF estén lo suficientemente espaciadas como para que no interfieran entre sí y arruinen el ajuste.
En ImageJ, podemos aproximarnos mas o menos a esta localización dibujando un perfil de línea a través del pico de una PSF y luego ejecutando . Allí podemos ajustar una función gaussiana 1D, para la cual la ecuación utilizada es
\(a\) es simplemente una constante de fondo, \(b\) indica la amplitud del pico (es decir, el valor máximo de la gaussiana con el fondo restado), y \(c\) da la ubicación del pico a lo largo de la línea del perfil. Pero tal vez el parámetro más útil aquí es \(d\), que corresponde al valor \(\sigma\) de un filtro gaussiano. Así que si conoces este valor para una PSF, puedes aproximar la misma cantidad de desenfoque con un filtro Gaussiano. Esto puede ser útil en Simulando la formación de imágenes.

